Greatest common divisor
The greatest common divisor (GCD) of a set of integers is the greatest integer that divides all the integers in the set, unless the set contains only zeroes, in which the GCD is defined to be zero. For example, the GCD of 12 and 20 is 4, because 4 divides both 12 and 20, and no integer larger than 4 divides both 12 and 20. The GCD is also sometimes called the greatest common factor (GCF) (perhaps because it avoids confusing schoolchildren with two different meanings of the word divisor).
Contents
Properties
-
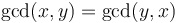 (commutativity)
(commutativity) -
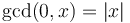
-
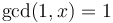
-
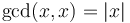
- All common divisors of a set of integers divide the GCD of that set. For example, the common divisors of 24 and 42 are -6, -3, -2, -1, 1, 2, 3, and 6, and the GCD is 6. Notice that all the common divisors are also divisors of 6.
- The GCD is never negative, because if
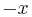 is a common divisor, then so is
is a common divisor, then so is 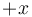 . Also,
. Also, 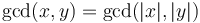 .
. - If
 and
and  are sets, then
are sets, then 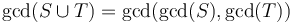 . For example,
. For example, 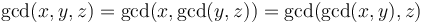 (associativity).
(associativity). -
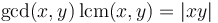 .
. -
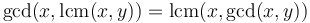 . (This property is the absorption law of the lattice over the positive integers with GCD as meet and LCM as join.)
. (This property is the absorption law of the lattice over the positive integers with GCD as meet and LCM as join.) - If
 has prime factorization
has prime factorization 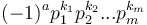 and
and  has prime factorization
has prime factorization 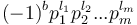 , then
, then 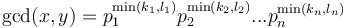 . Therefore, it is possible to find the GCD of two integers by factorizing them; but much more efficient methods exist.
. Therefore, it is possible to find the GCD of two integers by factorizing them; but much more efficient methods exist. -
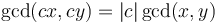 whenever
whenever 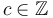 .
. -
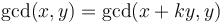 for any
for any 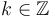 .
. - There exist integers
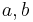 such that
such that 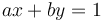 if and only if
if and only if 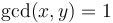 . (This is called Bézout's identity. We will not prove it directly, but we will exhibit an algorithm for determining
. (This is called Bézout's identity. We will not prove it directly, but we will exhibit an algorithm for determining  and
and  .)
.)
Euclidean algorithm
Means of computing the GCD of two integers efficiently have been known since antiquity. The well-known Euclidean algorithm uses the property that 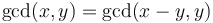 for any
for any 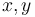 . When given two positive integers, we repeatedly subtract the smaller from the larger, thus reducing the size of the larger integer; and we repeat this until the two integers become identical. For example,
. When given two positive integers, we repeatedly subtract the smaller from the larger, thus reducing the size of the larger integer; and we repeat this until the two integers become identical. For example, 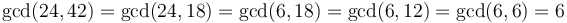 . The following is a naive implementation:
. The following is a naive implementation:
int gcd(int x, int y) { if (x < 0) x = -x; if (y < 0) y = -y; if (x == 0) return x; if (y == 0) return y; if (x == y) return x; if (x > y) return gcd(x - y, x); else return gcd(x, y - x); }
In practice, negative numbers are rarely encountered. Also, when we obtain two identical integers, if we perform one additional subtraction, we will get zero, which we have to handle in any case, so:
int gcd(int x, int y) { if (x == 0 || y == 0) return x + y; if (x >= y) return gcd(x - y, y); else return gcd(x, y - x); }
To speed this up, we note that if we start out with 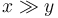 , then the final result of subtracting
, then the final result of subtracting  from
from  over and over again will be the least non-negative residue of
over and over again will be the least non-negative residue of  modulo
modulo  . Hence, instead of performing repeated subtraction, we use the mod operator. Finally, with some cleverness, we obtain this common form:
. Hence, instead of performing repeated subtraction, we use the mod operator. Finally, with some cleverness, we obtain this common form:
int gcd(int x, int y) { if (x == 0) return y; else return gcd(y%x, x); }
Also, although we have written this algorithm recursively, we can also write it iteratively, since it is tail recursive:
while (x > 0) { y %= x; swap(x, y); } /* y now contains the GCD of original (x, y) */
Now, regarding performance:
Theorem: The GCD of two positive integers  and
and  can be computed using the Euclidean algorithm in
can be computed using the Euclidean algorithm in 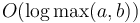 mod operations.
mod operations.
Sketch Proof: The idea is to use induction on  . Without loss of generality, we assume
. Without loss of generality, we assume 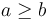 . Then, there are two possibilities. If
. Then, there are two possibilities. If 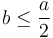 , then
, then 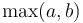 will be cut at least in half after the first mod operation. But if
will be cut at least in half after the first mod operation. But if 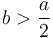 , then
, then  goes into
goes into  only once, and we obtain
only once, and we obtain 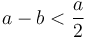 and
and  after the first mod operation; a second will then take
after the first mod operation; a second will then take  below
below 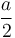 . So in either case, after at most two mod operations,
. So in either case, after at most two mod operations, 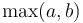 is reduced by at least a factor of 2.
is reduced by at least a factor of 2.
Note: A more careful analysis shows that the worst-case number of mod operations required to find 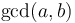 using the Euclidean algorithm goes approximately as
using the Euclidean algorithm goes approximately as 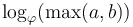 , where
, where 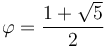 .
.
The bit complexity of the Euclidean algorithm is 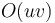 , so that finding the GCD of two large numbers with
, so that finding the GCD of two large numbers with  and
and  bits, respectively, requires
bits, respectively, requires 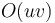 time.[1] For two numbers of approximately equal length
time.[1] For two numbers of approximately equal length  , this is
, this is 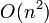 . By comparison, the straightforward algorithm based on factorizing the input integers does not run in polynomial time, and hence will perform far worse for large
. By comparison, the straightforward algorithm based on factorizing the input integers does not run in polynomial time, and hence will perform far worse for large  .
.
Extended Euclidean algorithm
The extended Euclidean algorithm is the name given to the well-known procedure used to find integer solutions to the equation 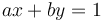 , where
, where  and
and  are given with
are given with 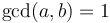 . For example, we can use it to solve the equation
. For example, we can use it to solve the equation 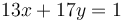 for
for  and
and  (one possible solution is
(one possible solution is 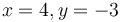 .
.
This equation only has solutions when 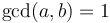 , because if
, because if 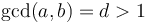 , then
, then 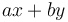 will always be divisible by
will always be divisible by 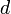 , and hence can never be 1. However, in this case
, and hence can never be 1. However, in this case 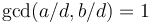 , so we can find solutions to the equation
, so we can find solutions to the equation 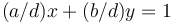 , that is,
, that is, 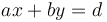 . So in general we can always solve
. So in general we can always solve 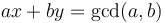 in integers.
in integers.
The reason why this is known as the extended Euclidean algorithm is that it is based on reducing  and
and  as in the Euclidean algorithm, recursively, until they become small enough so that the equation is easy to solve; then reconstructing the solution to the original equation using the results.
as in the Euclidean algorithm, recursively, until they become small enough so that the equation is easy to solve; then reconstructing the solution to the original equation using the results.
In particular, when we take the remainder of  modulo
modulo  and obtain
and obtain  , this tells us that
, this tells us that 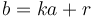 for some integer
for some integer  . So each step of the Euclidean algorithm expresses the fact that
. So each step of the Euclidean algorithm expresses the fact that 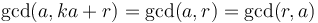 .
.
Now suppose we can find integers 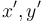 such that
such that 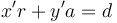 . Then, recall that
. Then, recall that 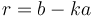 ; therefore,
; therefore, 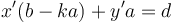 . Expanding, we obtain
. Expanding, we obtain 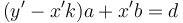 . So set
. So set 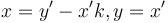 , and we now have a solution to
, and we now have a solution to 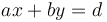 .
.
This suggests that, in general, to solve 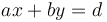 , we first compute quotient
, we first compute quotient  and remainder
and remainder  when
when  is divided by
is divided by  ; and then (recursively) find some solution to
; and then (recursively) find some solution to 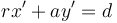 ; and finally obtain
; and finally obtain 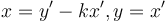 .
.
This gives the following implementation, where we assume that  and
and  are positive:
are positive:
/* Returns the GCD. */ int gcd_extended(int a, int b, int* x, int* y) { if (a == 0) { *x = 0, *y = 1; /* 0(0) + 1(b) = b = gcd(a,b) */ return b; } else { int k = b/a; int r = b%a; int _x, _y; int d = gcd_extended(r, a, &_x, &_y); *x = _y - k*_x; *y = _x; return d; } }
One specific application of the extended Euclidean algorithm is that of computing modular inverses. That is, given some integer 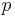 and some modulus
and some modulus 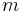 , we wish to find another integer
, we wish to find another integer 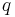 such that
such that 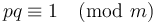 . For example, if
. For example, if 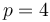 and
and 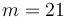 , then
, then 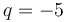 works, since
works, since 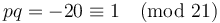 .
.
All we need to do to solve this is to note that the statement that 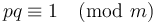 is equivalent to
is equivalent to 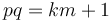 for some integer
for some integer  , or
, or 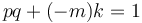 , to be solved for integers
, to be solved for integers 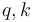 (even though we might not care what
(even though we might not care what  is). We then use the extended Euclidean algorithm. Note that this suggests that a solution exists only when
is). We then use the extended Euclidean algorithm. Note that this suggests that a solution exists only when 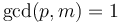 , which is indeed the case.
, which is indeed the case.
Binary GCD algorithm
This is another popular GCD algorithm, also recursive.
- If
 and
and  are both even, then
are both even, then 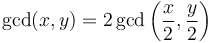 .
. - If
 is even, but
is even, but  is odd, then
is odd, then 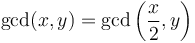 . This is because every common divisor of
. This is because every common divisor of  and
and  is odd, and hence will also divide
is odd, and hence will also divide 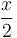 .
. - If
 and
and  are both odd, then
are both odd, then 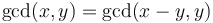 , as always.
, as always.
This suggests the following naive implementation, assuming that  and
and  are both nonnegative:
are both nonnegative:
int gcd(int x, int y) { if (x == 0) return y; if (x < y) return gcd(y, x); if (x%2 == 1) if (y%2 == 1) return gcd(x - y, y); else return gcd(x, y/2); else if (y%2 == 1) return gcd(x/2, y); else return gcd(x/2, y/2)*2; }
Computing the GCD of  and
and  using this algorithm will take
using this algorithm will take 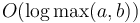 steps, just as the Euclidean algorithm. This becomes clear when we write out the binary representations of
steps, just as the Euclidean algorithm. This becomes clear when we write out the binary representations of  and
and  :
:
- If either
 or
or  is even, then it will be divided by two, which reduces its length by one.
is even, then it will be divided by two, which reduces its length by one. - If both
 and
and  are odd, then one of them will become even after a subtraction, and then it will be divided by two, which again reduces its length by one. In effect
are odd, then one of them will become even after a subtraction, and then it will be divided by two, which again reduces its length by one. In effect 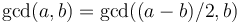 (for the case
(for the case  ).
).
Therefore, we obtain a bound of 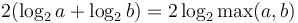 iterations, since after every two iterations it is guaranteed that the binary length of at least one of the two numbers is reduced.
iterations, since after every two iterations it is guaranteed that the binary length of at least one of the two numbers is reduced.
Furthermore, each operation (either halving an even integer, or performing a subtraction) has bit complexity proportional to the length of the integers involved. If we halve  , then
, then 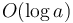 time is required for this step; if we subtract
time is required for this step; if we subtract  from
from  , then
, then 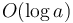 time is required for this step, and in the next step
time is required for this step, and in the next step  will be halved, also requiring
will be halved, also requiring 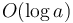 time. So at most
time. So at most 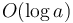 operations of
operations of 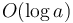 bit complexity each can be performed on
bit complexity each can be performed on  , and at most
, and at most 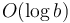 operations of
operations of 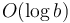 bit complexity each; so the overall bit complexity is
bit complexity each; so the overall bit complexity is 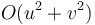 , where
, where 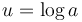 and
and 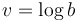 . This will often be expressed as
. This will often be expressed as 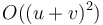 (quadratic in total input size) or
(quadratic in total input size) or 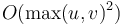 , matching the bound on the Euclidean algorithm.
, matching the bound on the Euclidean algorithm.
The binary GCD algorithm can be considered to be motivated by the fact that reduction modulo 2, division by 2, and subtraction admit simpler bit complexities than the general modulo operation that the Euclidean algorithm uses, which suggests that it should be faster in practice. However, the naive implementation shown above is unlikely to outperform the optimized Euclidean algorithm in the previous section; optimization is required in order for the binary GCD algorithm to be competitive.
References
- ↑ Jeffrey Shallit. The Greatest Common Divisor, pp. 22-22. CMI Introductory Workshop, Algorithmic Number Theory. Retrieved from www.cs.uwaterloo.ca/~shallit/Talks/gcd.ps