Longest palindromic subsequence
Not to be confused with Longest palindromic substring.
The longest palindromic subsequence problem is the problem of finding the longest subsequence of a string (a subsequence is obtained by deleting some of the characters from a string without reordering the remaining characters) which is also a palindrome. In general, the longest palindromic subsequence is not unique. For example, the string alfalfa has two palindromic subsequences of length 5: alala and afafa. However, it does not have any palindromic subsequences longer than five characters. Therefore alala and afafa are both considred longest palindromic subsequences of alfalfa.
Contents
Precise statement
Three variations of this problem may be distinguished:
- Find the maximum possible length for a palindromic subsequence.
- Find some palindromic subsequence of maximal length.
- Find all longest palindromic subsequences.
Theorem: Returning all longest palindromic subsequences cannot be accomplished in worst-case polynomial time.
Proof[1]: Consider a string made up of 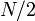 ones, followed by
ones, followed by 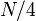 zeroes, and finally
zeroes, and finally 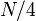 ones. (Assume
ones. (Assume  is a multiple of 4, although it does not really matter.) Any palindromic substring either does not contain any zeroes, in which case its length is only up to
is a multiple of 4, although it does not really matter.) Any palindromic substring either does not contain any zeroes, in which case its length is only up to 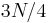 , or it contains at least one zero. If it contains at least one zero, it must be of the form
, or it contains at least one zero. If it contains at least one zero, it must be of the form 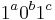 , but
, but  and
and  must be equal. (This is because the middle of the palindrome must lie somewhere within the zeroes, otherwise there would be no zeroes on one side of it and at least one zero on the other side; but as long as the middle lies within the zeroes, there must be an equal number of ones on each side.) But
must be equal. (This is because the middle of the palindrome must lie somewhere within the zeroes, otherwise there would be no zeroes on one side of it and at least one zero on the other side; but as long as the middle lies within the zeroes, there must be an equal number of ones on each side.) But  can only be up to
can only be up to 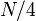 , and likewise with
, and likewise with  , so again the palindrome cannot be longer than
, so again the palindrome cannot be longer than 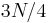 characters. However, there are
characters. However, there are 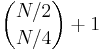 palindromic substrings of length
palindromic substrings of length 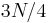 ; we can either take all the ones, or we can take all
; we can either take all the ones, or we can take all 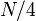 zeroes, all
zeroes, all 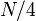 terminal ones, and
terminal ones, and 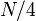 out of the
out of the 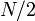 initial ones. Thus the output size is not polynomial in
initial ones. Thus the output size is not polynomial in  , and then neither can the algorithm be in the worst case.
, and then neither can the algorithm be in the worst case. 
However, this does not rule out the existence of a polynomial-time algorithm for the first two variations on the problem. We now present such an algorithm.
Theoretical background
(Note: these Lemmas are "obvious" and their proofs will probably not help you intuitively understand how the algorithm works, so skip them if they are too heavy in mathematical notation for you.)
Lemma 1: Any palindromic subsequence  of a string
of a string  is a common subsequence of
is a common subsequence of  and its reverse
and its reverse 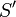 .
.
Proof: Since  is a subsequence of
is a subsequence of  , its reverse
, its reverse 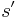 is a subsequence of
is a subsequence of 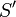 But
But 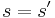 since
since  is a palindrome, so
is a palindrome, so  is a subsequence of
is a subsequence of 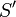 , and hence a common subsequence.
, and hence a common subsequence. 
Lemma 2: If there exists a common subsequence  of length
of length 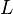 of
of  and its reverse
and its reverse 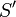 , then there exists a palindromic subsequence
, then there exists a palindromic subsequence 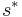 of
of  of length greater than or equal to
of length greater than or equal to 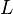 which is a supersequence of
which is a supersequence of  .
.
Proof: Let  denote the subsequence in
denote the subsequence in  and
and 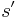 denote the subsequence in
denote the subsequence in 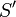 . Let
. Let 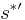 denote a supersequence of
denote a supersequence of 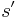 . Walk through the string
. Walk through the string  from left to right. that is, consider
from left to right. that is, consider 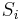 as
as  goes from 0 to
goes from 0 to 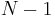 . Let
. Let 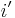 denote
denote 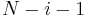 , so that
, so that  at all times. For each value of
at all times. For each value of  :
:
- If
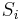 is in
is in  then
then 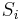 is in
is in 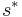 and
and 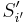 is in
is in 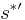 .
. - If
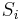 is not in
is not in  but
but 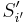 is in
is in 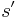 , then, again,
, then, again, 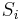 is in
is in 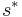 and
and 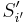 is in
is in 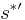 .
. - Otherwise,
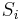 is not in
is not in 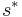 and
and 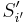 is not in
is not in 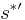 .
.
After this has completed, 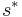 is clearly a supersequence of
is clearly a supersequence of  and a subsequence of
and a subsequence of  , and likewise
, and likewise 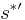 is a supersequence of
is a supersequence of 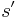 and a subsequence of
and a subsequence of 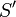 .
.
Furthermore, 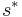 and
and 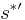 are reverses of each other, because whenever a character
are reverses of each other, because whenever a character 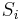 is added to the end of
is added to the end of 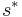 , the identical character
, the identical character 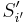 is added to the beginning of
is added to the beginning of 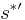 , and vice versa.
, and vice versa.
Now consider the  th character in
th character in 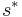 . This is
. This is 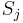 where
where  is the
is the  th smallest index for which either
th smallest index for which either 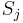 is in
is in  or
or 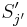 is in
is in 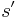 . This means that
. This means that 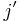 is the
is the  th largest index for which either
th largest index for which either 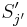 is in
is in 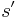 or
or 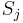 is in
is in  , since
, since  and
and 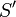 are reverses of each other. Therefore,
are reverses of each other. Therefore, 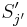 is the
is the  th character in
th character in 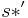 (characters near the beginning of
(characters near the beginning of 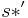 originate from near the beginning of
originate from near the beginning of 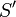 or the end of
or the end of  ). But the
). But the  th character in
th character in 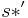 is the
is the 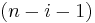 st character in
st character in 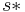 , because
, because 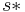 and
and 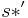 are reverses of each other. Therefore
are reverses of each other. Therefore 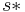 is palindromic.
is palindromic. 
Theorem: Any longest common subsequence  of
of  and its reverse
and its reverse 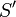 is a longest palindromic subsequence of
is a longest palindromic subsequence of  .
.
Proof: Suppose  is not palindromic. By Lemma 2, we know we can obtain a palindrome
is not palindromic. By Lemma 2, we know we can obtain a palindrome 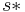 that is a supersequence of
that is a supersequence of  and a subsequence of
and a subsequence of  . This cannot be
. This cannot be  itself since
itself since  is not palindromic. So
is not palindromic. So 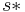 must be longer than
must be longer than  . By Lemma 1,
. By Lemma 1, 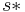 is a common subsequence of
is a common subsequence of  and
and 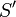 . However, as
. However, as 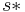 is longer than
is longer than  , this contradicts
, this contradicts  having been a longest common subsequence of
having been a longest common subsequence of  and
and 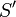 .
.
Likewise, suppose  is a longest common subsequence of
is a longest common subsequence of  and
and 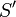 and palindromic but it is not a longest palindromic subsequence of
and palindromic but it is not a longest palindromic subsequence of  . Then there again exists a longer palindromic subsequence of
. Then there again exists a longer palindromic subsequence of  , which gives a longer common subsequence of
, which gives a longer common subsequence of  and
and 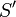 , a contradiction.
, a contradiction. 
Algorithm
A corollary of the Theorem is that a longest palindromic subsequence of  can be found in
can be found in 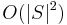 time simply by finding the longest common subsequence of
time simply by finding the longest common subsequence of  and its reverse.
and its reverse.
Note that there exist more efficient algorithms for finding longest common subsequences, which also give more efficient means of computing longest palindromic subsequences.
Shortest palindromic supersequence
It can also be shown that the shortest palindromic supersequence of a string  can be found by taking the shortest common supersequence of
can be found by taking the shortest common supersequence of  and its reverse. The proof is left as an exercise to the reader.
and its reverse. The proof is left as an exercise to the reader.
References
- ↑ Jonathan T. Schneider (2010). Personal communication.