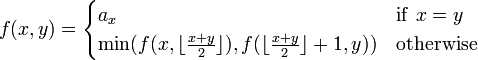Difference between revisions of "Segment tree"
m (→Query) |
|||
| Line 44: | Line 44: | ||
===Query=== | ===Query=== | ||
[[File:Segtree_query_92631587.png|200px|thumb|right|Only the two nodes marked in yellow must be accessed to find the minimum of the elements corresponding to the leaves marked in grey.]] | [[File:Segtree_query_92631587.png|200px|thumb|right|Only the two nodes marked in yellow must be accessed to find the minimum of the elements corresponding to the leaves marked in grey.]] | ||
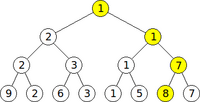
| − | To ''query'' a segment tree is to use it to determine a function of a range in the underlying array (in this case, the minimum element of that range). The execution of a query is more complex than the execution of an update and will be illustrated by example. Suppose we wish to know the minimum element between the first and sixth, inclusive. We shall represent this query as <math>f(1,6)</math>. Each node in the segment tree contains the minimum in some interval: for example, the root node contains <math>f(1,8)</math>, its left child <math>f(1,4)</math>, its right <math>f(5,8)</math>, and so on, with each leaf containing <math>f(x,x)</math> for some <math>x</math>. There is no node that contains <math>f(1,6)</math>, but we notice that <math>f(1,6) = \min(f(1,4),f(5,6))</math>, and that there ''are'' nodes in the segment tree containing those two values (shown in yellow). (This expression for <math>f(1,6)</math> is not the one given by the definition of <math>f</math>, but it is fairly clear that <math>f(x,y) = \min(f(x,z),f(z+1,y))</math> where <math>x \le z | + | To ''query'' a segment tree is to use it to determine a function of a range in the underlying array (in this case, the minimum element of that range). The execution of a query is more complex than the execution of an update and will be illustrated by example. Suppose we wish to know the minimum element between the first and sixth, inclusive. We shall represent this query as <math>f(1,6)</math>. Each node in the segment tree contains the minimum in some interval: for example, the root node contains <math>f(1,8)</math>, its left child <math>f(1,4)</math>, its right <math>f(5,8)</math>, and so on, with each leaf containing <math>f(x,x)</math> for some <math>x</math>. There is no node that contains <math>f(1,6)</math>, but we notice that <math>f(1,6) = \min(f(1,4),f(5,6))</math>, and that there ''are'' nodes in the segment tree containing those two values (shown in yellow). (This expression for <math>f(1,6)</math> is not the one given by the definition of <math>f</math>, but it is fairly clear that <math>f(x,y) = \min(f(x,z),f(z+1,y))</math> where <math>x \le z < y</math>, regardless of the actual value of <math>z</math>.)<br/> |
When querying a segment tree, therefore, we select a subset of the nodes with the property that the union of their sets of descendants is exactly the interval whose minimum we seek. To do so, we start at the root and recurse over nodes whose corresponding intervals have at least one element in common with the query interval. Hence, in our example of <math>f(1,6)</math>, we notice that both the left and right subtrees contain descendants that contain elements in the query interval; hence, we recurse on both. The left child of the root serves as a base case, since its interval is contained entirely within the query interval; hence it is chosen (marked in yellow). At the right child of the root, we notice that its left child has descendants in the query interval, but its right does not; hence we recurse on the former and not the latter. The former is now another base case, and it too is chosen and marked in yellow. The recursion has now terminated, and the desired minimum is the minimum of the nodes that have been chosen. | When querying a segment tree, therefore, we select a subset of the nodes with the property that the union of their sets of descendants is exactly the interval whose minimum we seek. To do so, we start at the root and recurse over nodes whose corresponding intervals have at least one element in common with the query interval. Hence, in our example of <math>f(1,6)</math>, we notice that both the left and right subtrees contain descendants that contain elements in the query interval; hence, we recurse on both. The left child of the root serves as a base case, since its interval is contained entirely within the query interval; hence it is chosen (marked in yellow). At the right child of the root, we notice that its left child has descendants in the query interval, but its right does not; hence we recurse on the former and not the latter. The former is now another base case, and it too is chosen and marked in yellow. The recursion has now terminated, and the desired minimum is the minimum of the nodes that have been chosen. | ||
Revision as of 20:15, 29 December 2009
The segment tree is a highly versatile data structure, based upon the divide-and-conquer paradigm, which can be thought of as a tree of intervals of an underlying array, constructed so that queries on ranges of the array as well as modifications to the array's elements may be efficiently performed.
Contents
Motivation
One of the most common applications of the segment tree is the solution to the range minimum query problem. In this problem, we are given some array and repeatedly asked to find the minimum value within some specified range of indices. For example, if we are given the array ![[9,2,6,3,1,5,0,7]](/wiki/images/math/a/3/e/a3e4109270a19cac82c7e91bec7564e4.png) , we might be asked for the minimum element between the third and the sixth, inclusive, which would be
, we might be asked for the minimum element between the third and the sixth, inclusive, which would be 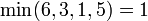 . Then, another query might ask for the minimum element between the first and third, inclusive, and we would answer 2, and so on. Various solutions to this problem are discussed in the range minimum query article, but the segment tree is often the most appropriate choice, especially when modification instructions are interspersed with the queries. For the sake of brevity, we shall focus for several following sections on the type of segment tree designed to answer the range minimum query without explicitly re-stating each time that we are doing so. Bear in mind, however, that other types of segment tree exist, which are discussed later in the article.
. Then, another query might ask for the minimum element between the first and third, inclusive, and we would answer 2, and so on. Various solutions to this problem are discussed in the range minimum query article, but the segment tree is often the most appropriate choice, especially when modification instructions are interspersed with the queries. For the sake of brevity, we shall focus for several following sections on the type of segment tree designed to answer the range minimum query without explicitly re-stating each time that we are doing so. Bear in mind, however, that other types of segment tree exist, which are discussed later in the article.
The divide-and-conquer solution
The divide-and-conquer solution would be as follows:
- If the range contains one element, that element itself is trivially the minimum within that range.
- Otherwise, divide the range into two smaller ranges, each approximately half the size of the original, and find their respective minima. The minimum for the original range is then the smaller of the two minima of the sub-ranges.
Hence, if 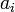 denotes the
denotes the  th element in the array, finding the minimum could be encoded as the following recursive function:
th element in the array, finding the minimum could be encoded as the following recursive function:
assuming that 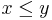 .
.
Hence, for example, the first query from the previous section would be 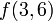 and it would be recursively evaluated as
and it would be recursively evaluated as 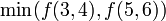 .
.
Structure
Suppose that we use the function defined above to evaluate 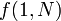 , where
, where  is the number of elements in the array. When
is the number of elements in the array. When  is large, this recursive call has two "children", one of which is the recursive call
is large, this recursive call has two "children", one of which is the recursive call 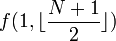 , and the other one of which is
, and the other one of which is 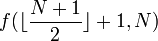 . Each of these children will then have two children of its own, and so on, down until the base case is reached. If we represent these recursive calls with a tree structure, the call
. Each of these children will then have two children of its own, and so on, down until the base case is reached. If we represent these recursive calls with a tree structure, the call 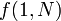 would be the root, it would have two children, each child would have two more children, and so on; the base cases would be the leaves of the tree. We are now ready to specify the structure of the segment tree:
would be the root, it would have two children, each child would have two more children, and so on; the base cases would be the leaves of the tree. We are now ready to specify the structure of the segment tree:
- it is a binary tree which represents some underlying array;
- each node is associated with some interval of the array and contains the value(s) of one or more functions of the elements in that interval;
- the root node is associated with the entire array (i.e. the interval
![[1,N]](/wiki/images/math/a/2/8/a287d2f128be5adc41f2ea0249d39045.png) );
); - each leaf is associated with an individual element;
- each non-leaf node has two children whose associated intervals are disjoint, and the union of the intervals associated with the two children is the interval associated with the parent;
- each child's interval has approximately half the size of the parent's interval;
- the data stored in each non-leaf node is not only a function of the elements in its associated interval but also a function of the data stored in its children.
That is, the structure of the segment tree is exactly that of the recursive call tree of the function  defined above (up to some minor details, such as whether the middle element of an interval of odd size belongs to the left child interval or the right).
defined above (up to some minor details, such as whether the middle element of an interval of odd size belongs to the left child interval or the right).
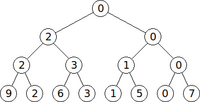
Hence, for example, the root node of the array ![[9,2,6,3,1,5,0,7]](/wiki/images/math/a/3/e/a3e4109270a19cac82c7e91bec7564e4.png) would contain the number 0: the minimum of the entire array. Its left child would contain the minimum of
would contain the number 0: the minimum of the entire array. Its left child would contain the minimum of ![[9,2,6,3]](/wiki/images/math/8/4/b/84b2b8698c67105233fed595d56323d7.png) , that is, 2, and the right would contain the minimum of
, that is, 2, and the right would contain the minimum of ![[1,5,0,7]](/wiki/images/math/3/f/7/3f74c03e69ea78f1964137a87a0e88b2.png) , that is, 0. Evidently, the datum stored in the root node, 0, is the minimum of the data stored at its immediate children, 0 and 2. Similarly, the datum 2 stored in the left child is the minimum of the data stored at its immediate children, 2 and 3 (which are the minima in
, that is, 0. Evidently, the datum stored in the root node, 0, is the minimum of the data stored at its immediate children, 0 and 2. Similarly, the datum 2 stored in the left child is the minimum of the data stored at its immediate children, 2 and 3 (which are the minima in ![[9,2]](/wiki/images/math/e/4/d/e4d830bf7280ee64ce69250c7fadb25c.png) and
and ![[6,3]](/wiki/images/math/f/9/1/f9141fbc368a52657b6060cddac6a108.png) , respectively). Each individual element in the array has a leaf node, which merely contains that element itself. (The minimum of a range containing a single element is, of course, the element itself.)
, respectively). Each individual element in the array has a leaf node, which merely contains that element itself. (The minimum of a range containing a single element is, of course, the element itself.)
Operations
There are three fundamental operations on a segment tree.
Construction
To construct a segment tree is to initialize it so that it represents some array; we can query and modify this array later but first we need to construct a valid segment tree. We can construct a segment tree either top-down or bottom-up. Top-down construction is recursive; we attempt to fill in the root node, which leads to a recursive call on each of the two children, and so on; the base cases are the leaf nodes, which may be immediately filled in with the corresponding values from the array. After the two recursive calls made on behalf of a non-leaf node return, that node's value is set to the minimum of the values stored at the children. Bottom-up construction is left as an exercise for the reader; the difference in speed is likely to be negligible.
Update
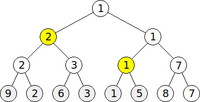
To update a segment tree is to modify the value of one element in the underlying array. To do so, we first modify the corresponding leaf node. The other leaf nodes are not affected, since each leaf node is associated only with an individual element. The modified node's parent is affected, since its associated interval contains the modified element, and so is the grandparent, and so on up to the root, but no other nodes are affected. To execute a top-down update, we begin by requesting an update of the root; this leads to a recursive call of one of the two children --- the one whose associated interval contains the modified element. (The other child and its subtree are unaffected.) The same is done recursively for the child; the base case is the leaf node associated with the element to update. After a recursive call has completed, the value in a non-leaf node is re-evaluated as the minimum of the values at its two children. Updating a segment tree bottom-up is possible too and is again left as an exercise for the reader.
Query
To query a segment tree is to use it to determine a function of a range in the underlying array (in this case, the minimum element of that range). The execution of a query is more complex than the execution of an update and will be illustrated by example. Suppose we wish to know the minimum element between the first and sixth, inclusive. We shall represent this query as 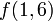 . Each node in the segment tree contains the minimum in some interval: for example, the root node contains
. Each node in the segment tree contains the minimum in some interval: for example, the root node contains 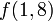 , its left child
, its left child 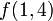 , its right
, its right 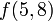 , and so on, with each leaf containing
, and so on, with each leaf containing 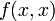 for some
for some  . There is no node that contains
. There is no node that contains 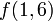 , but we notice that
, but we notice that 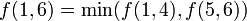 , and that there are nodes in the segment tree containing those two values (shown in yellow). (This expression for
, and that there are nodes in the segment tree containing those two values (shown in yellow). (This expression for 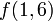 is not the one given by the definition of
is not the one given by the definition of  , but it is fairly clear that
, but it is fairly clear that 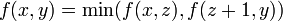 where
where 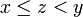 , regardless of the actual value of
, regardless of the actual value of 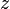 .)
.)
When querying a segment tree, therefore, we select a subset of the nodes with the property that the union of their sets of descendants is exactly the interval whose minimum we seek. To do so, we start at the root and recurse over nodes whose corresponding intervals have at least one element in common with the query interval. Hence, in our example of 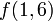 , we notice that both the left and right subtrees contain descendants that contain elements in the query interval; hence, we recurse on both. The left child of the root serves as a base case, since its interval is contained entirely within the query interval; hence it is chosen (marked in yellow). At the right child of the root, we notice that its left child has descendants in the query interval, but its right does not; hence we recurse on the former and not the latter. The former is now another base case, and it too is chosen and marked in yellow. The recursion has now terminated, and the desired minimum is the minimum of the nodes that have been chosen.
, we notice that both the left and right subtrees contain descendants that contain elements in the query interval; hence, we recurse on both. The left child of the root serves as a base case, since its interval is contained entirely within the query interval; hence it is chosen (marked in yellow). At the right child of the root, we notice that its left child has descendants in the query interval, but its right does not; hence we recurse on the former and not the latter. The former is now another base case, and it too is chosen and marked in yellow. The recursion has now terminated, and the desired minimum is the minimum of the nodes that have been chosen.