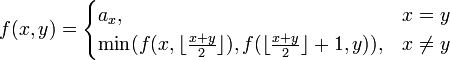Difference between revisions of "Segment tree"
| Line 1: | Line 1: | ||
The '''segment tree''' is a highly versatile data structure, based upon the [[Divide and conquer|divide-and-conquer]] paradigm, which can be thought of as a tree of intervals of an underlying array, constructed so that queries on ranges of the array as well as modifications to the array's elements may be efficiently performed. | The '''segment tree''' is a highly versatile data structure, based upon the [[Divide and conquer|divide-and-conquer]] paradigm, which can be thought of as a tree of intervals of an underlying array, constructed so that queries on ranges of the array as well as modifications to the array's elements may be efficiently performed. | ||
| + | |||
| + | ==Motivation== | ||
| + | One of the most common applications of the segment tree is the solution to the [[range minimum query]] problem. In this problem, we are given some array and repeatedly asked to find the minimum value within some specified range of indices. For example, if we are given the array [9,2,6,3,1,5,0,7], we might be asked for the minimum element between the third and the sixth, inclusive, which would be <math>\operatorname{min}(6,3,1,5) = 1</math>. Then, another query might ask for the minimum element between the first and third, inclusive, and we would answer 2, and so on. Various solutions to this problem are discussed in the [[range minimum query]] article, but the segment tree is often the most appropriate choice, especially when modification instructions are interspersed with the queries. | ||
| + | |||
| + | ===The divide-and-conquer solution=== | ||
| + | The divide-and-conquer solution would be as follows: | ||
| + | * If the range contains one element, that element itself is trivially the minimum within that range. | ||
| + | * Otherwise, divide the range into two smaller ranges, each approximately half the size of the original, and find their respective minima. The minimum for the original range is then the smaller of the two minima of the sub-ranges. | ||
| + | Hence, if <math>a_i</math> denotes the <math>i</math><sup>th</sup> element in the array, finding the minimum could be encoded as the following recursive function: | ||
| + | :<math>\displaystyle | ||
| + | f(x,y) = | ||
| + | \begin{cases} | ||
| + | a_x , & x = y \\ | ||
| + | \min(f(x,\lfloor\frac{x+y}{2}\rfloor),f(\lfloor\frac{x+y}{2}\rfloor+1,y)) , & x \neq y \\ | ||
| + | \end{cases} | ||
| + | </math> | ||
| + | assuming that <math>x \le y</math>.<br/> | ||
| + | Hence, for example, the first query from the previous section would be <math>f(3,6)</math> and it would be recursively evaluated as <math>\min(f(3,4),f(5,6))</math>. | ||
| + | |||
| + | <!-- | ||
==The problem== | ==The problem== | ||
| Line 7: | Line 27: | ||
One could merely store the array of numbers as a simple array, updating in <math>\mathcal{O}(1)</math> time whenever necessary and querying by looping over the range specified, adding the elements contained within. This latter step, however, can take <math>\mathcal{O}(N)</math> time when the size of the range is <math>\mathcal{O}(N)</math>. It is also possible to store the [[prefix sum]]s of the array, so that queries can be performed in <math>\mathcal{O}(1)</math> time but updates can take <math>\mathcal{O}(1)</math> when the element to be updated is near the end of the array. Thus, if the number of queries is low compared to the number of queries, the former solution might be practical; similarly, if there are many more queries than updates, the latter might be practical. However, what if there are an approximately equal number of queries and updates? | One could merely store the array of numbers as a simple array, updating in <math>\mathcal{O}(1)</math> time whenever necessary and querying by looping over the range specified, adding the elements contained within. This latter step, however, can take <math>\mathcal{O}(N)</math> time when the size of the range is <math>\mathcal{O}(N)</math>. It is also possible to store the [[prefix sum]]s of the array, so that queries can be performed in <math>\mathcal{O}(1)</math> time but updates can take <math>\mathcal{O}(1)</math> when the element to be updated is near the end of the array. Thus, if the number of queries is low compared to the number of queries, the former solution might be practical; similarly, if there are many more queries than updates, the latter might be practical. However, what if there are an approximately equal number of queries and updates? | ||
| − | === | + | ===The segment tree=== |
| + | |||
| + | --> | ||
Revision as of 04:04, 27 December 2009
The segment tree is a highly versatile data structure, based upon the divide-and-conquer paradigm, which can be thought of as a tree of intervals of an underlying array, constructed so that queries on ranges of the array as well as modifications to the array's elements may be efficiently performed.
Motivation
One of the most common applications of the segment tree is the solution to the range minimum query problem. In this problem, we are given some array and repeatedly asked to find the minimum value within some specified range of indices. For example, if we are given the array [9,2,6,3,1,5,0,7], we might be asked for the minimum element between the third and the sixth, inclusive, which would be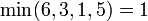 
. Then, another query might ask for the minimum element between the first and third, inclusive, and we would answer 2, and so on. Various solutions to this problem are discussed in the range minimum query article, but the segment tree is often the most appropriate choice, especially when modification instructions are interspersed with the queries.
The divide-and-conquer solution
The divide-and-conquer solution would be as follows:
- If the range contains one element, that element itself is trivially the minimum within that range.
- Otherwise, divide the range into two smaller ranges, each approximately half the size of the original, and find their respective minima. The minimum for the original range is then the smaller of the two minima of the sub-ranges.
Hence, if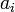 
denotes the 
th element in the array, finding the minimum could be encoded as the following recursive function:
assuming that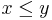 
.
Hence, for example, the first query from the previous section would be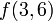 
and it would be recursively evaluated as 
.
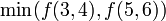