|
|
| Line 14: |
Line 14: |
| | | | |
| | However, this does not rule out the existence of a polynomial-time algorithm for the first two variations on the problem. We now present such an algorithm. | | However, this does not rule out the existence of a polynomial-time algorithm for the first two variations on the problem. We now present such an algorithm. |
| − |
| |
| − | ==Theoretical background==
| |
| − | (Note: these Lemmas are "obvious" and their proofs will probably not help you intuitively understand how the algorithm works, so skip them if they are too heavy in mathematical notation for you.)
| |
| − |
| |
| − | ''Lemma 1'': Any palindromic subsequence <math>s</math> of a string <math>S</math> is a common subsequence of <math>S</math> and its reverse <math>S'</math>.
| |
| − |
| |
| − | ''Proof'': Since <math>s</math> is a subsequence of <math>S</math>, its reverse <math>s'</math> is a subsequence of <math>S'</math> But <math>s = s'</math> since <math>s</math> is a palindrome, so <math>s</math> is a subsequence of <math>S'</math>, and hence a common subsequence. <math>_\blacksquare</math>
| |
| − |
| |
| − | ''Lemma 2'': If there exists a common subsequence <math>s</math> of length <math>L</math> of <math>S</math> and its reverse <math>S'</math>, then there exists a palindromic subsequence <math>s^*</math> of <math>S</math> of length greater than or equal to <math>L</math> which is a supersequence of <math>s</math>.
| |
| − |
| |
| − | ''This lemma is false'': Consider the sequence "abacbab" and its reverse, which has 6 (longest) common subsequences of length 5; "ababa", "babab", "bacab", "abcba", "abcab" and "bacba". The last two are obviously not palindromic, and there does not exist palindromic supersequences that are also subsequences of "abacbab".
| |
| − |
| |
| − | ''Proof'': Let <math>s</math> denote the subsequence in <math>S</math> and <math>s'</math> denote the subsequence in <math>S'</math>. Let <math>{s^*}'</math> denote a supersequence of <math>s'</math>. Walk through the string <math>S</math> from left to right. that is, consider <math>S_i</math> as <math>i</math> goes from 0 to <math>N-1</math>. Let <math>i'</math> denote <math>N-i-1</math>, so that <math>S_i = S'_{i'}</math> at all times. For each value of <math>i</math>:
| |
| − | * If <math>S_i</math> is in <math>s</math> then <math>S_i</math> is in <math>s^*</math> and <math>S'_{i'}</math> is in <math>{s^*}'</math>.
| |
| − | * If <math>S_i</math> is not in <math>s</math> but <math>S'_{i'}</math> is in <math>s'</math>, then, again, <math>S_i</math> is in <math>s^*</math> and <math>S'_{i'}</math> is in <math>{s^*}'</math>.
| |
| − | * Otherwise, <math>S_i</math> is not in <math>s^*</math> and <math>S'_{i'}</math> is not in <math>{s^*}'</math>.
| |
| − | After this has completed, <math>s^*</math> is clearly a supersequence of <math>s</math> and a subsequence of <math>S</math>, and likewise <math>{s^*}'</math> is a supersequence of <math>s'</math> and a subsequence of <math>S'</math>.
| |
| − |
| |
| − | Furthermore, <math>s^*</math> and <math>{s^*}'</math> are reverses of each other, because whenever a character <math>S_i</math> is added to the end of <math>s^*</math>, the identical character <math>S'_{i'}</math> is added to the beginning of <math>{s^*}'</math>, and ''vice versa''.
| |
| − |
| |
| − | Now consider the <math>i</math><sup>th</sup> character in <math>s^*</math>. This is <math>S_j</math> where <math>j</math> is the <math>i</math><sup>th</sup> smallest index for which either <math>S_j</math> is in <math>s</math> or <math>S'_{j'}</math> is in <math>s'</math>. This means that <math>j'</math> is the <math>i</math><sup>th</sup> largest index for which either <math>S'_{j'}</math> is in <math>s'</math> or <math>S_j</math> is in <math>s</math>, since <math>S</math> and <math>S'</math> are reverses of each other. Therefore, <math>S'_{j'}</math> is the <math>i</math><sup>th</sup> character in <math>{s^*}'</math> (characters near the beginning of <math>{s^*}'</math> originate from near the beginning of <math>S'</math> or the end of <math>S</math>). But the <math>i</math><sup>th</sup> character in <math>{s^*}'</math> is the <math>(n-i-1)</math><sup>st</sup> character in <math>s^*</math>, because <math>s^*</math> and <math>{s^*}'</math> are reverses of each other. Therefore <math>s^*</math> is palindromic. <math>_\blacksquare</math>
| |
| − |
| |
| − | '''Theorem''': Any [[longest common subsequence]] <math>s</math> of <math>S</math> and its reverse <math>S'</math> is a longest palindromic subsequence of <math>S</math>.
| |
| − |
| |
| − | '''Proof''': Suppose <math>s</math> is not palindromic. By Lemma 2, we know we can obtain a palindrome <math>s^*</math> that is a supersequence of <math>s</math> and a subsequence of <math>S</math>. This cannot be <math>s</math> itself since <math>s</math> is not palindromic. So <math>s^*</math> must be longer than <math>s</math>. By Lemma 1, <math>s^*</math> is a common subsequence of <math>S</math> and <math>S'</math>. However, as <math>s^*</math> is longer than <math>s</math>, this contradicts <math>s</math> having been a longest common subsequence of <math>S</math> and <math>S'</math>.
| |
| − |
| |
| − | Likewise, suppose <math>s</math> is a longest common subsequence of <math>S</math> and <math>S'</math> and palindromic but it is not a longest palindromic subsequence of <math>S</math>. Then there again exists a longer palindromic subsequence of <math>S</math>, which gives a longer common subsequence of <math>S</math> and <math>S'</math>, a contradiction. <math>_\blacksquare</math>
| |
| | | | |
| | ==Algorithm== | | ==Algorithm== |
| − | A corollary of the Theorem is that a longest palindromic subsequence of <math>S</math> can be found in <math>O(|S|^2)</math> time simply by finding the longest common subsequence of <math>S</math> and its reverse.
| + | todo |
| − | | + | |
| − | Note that there exist more efficient algorithms for finding longest common subsequences, which also give more efficient means of computing longest palindromic subsequences.
| + | |
| − | | + | |
| − | ==Shortest palindromic supersequence==
| + | |
| − | It can also be shown that the shortest palindromic supersequence of a string <math>S</math> can be found by taking the [[Longest_common_subsequence#Shortest_common_supersequence|shortest common supersequence]] of <math>S</math> and its reverse. The proof is left as an exercise to the reader.
| + | |
| | | | |
| | ==References== | | ==References== |
Revision as of 02:02, 27 May 2012
Not to be confused with Longest palindromic substring.
The longest palindromic subsequence problem is the problem of finding the longest subsequence of a string (a subsequence is obtained by deleting some of the characters from a string without reordering the remaining characters) which is also a palindrome. In general, the longest palindromic subsequence is not unique. For example, the string alfalfa has two palindromic subsequences of length 5: alala and afafa. However, it does not have any palindromic subsequences longer than five characters. Therefore alala and afafa are both considred longest palindromic subsequences of alfalfa.
Precise statement
Three variations of this problem may be distinguished:
- Find the maximum possible length for a palindromic subsequence.
- Find some palindromic subsequence of maximal length.
- Find all longest palindromic subsequences.
Theorem: Returning all longest palindromic subsequences cannot be accomplished in worst-case polynomial time.
Proof[1]: Consider a string made up of 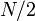 ones, followed by
ones, followed by 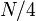 zeroes, and finally
zeroes, and finally 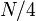 ones. (Assume
ones. (Assume  is a multiple of 4, although it does not really matter.) Any palindromic substring either does not contain any zeroes, in which case its length is only up to
is a multiple of 4, although it does not really matter.) Any palindromic substring either does not contain any zeroes, in which case its length is only up to 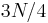 , or it contains at least one zero. If it contains at least one zero, it must be of the form
, or it contains at least one zero. If it contains at least one zero, it must be of the form 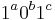 , but
, but 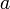 and
and 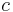 must be equal. (This is because the middle of the palindrome must lie somewhere within the zeroes, otherwise there would be no zeroes on one side of it and at least one zero on the other side; but as long as the middle lies within the zeroes, there must be an equal number of ones on each side.) But
must be equal. (This is because the middle of the palindrome must lie somewhere within the zeroes, otherwise there would be no zeroes on one side of it and at least one zero on the other side; but as long as the middle lies within the zeroes, there must be an equal number of ones on each side.) But 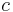 can only be up to
can only be up to 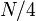 , and likewise with
, and likewise with 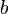 , so again the palindrome cannot be longer than
, so again the palindrome cannot be longer than 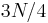 characters. However, there are
characters. However, there are 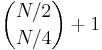 palindromic substrings of length
palindromic substrings of length 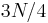 ; we can either take all the ones, or we can take all
; we can either take all the ones, or we can take all 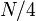 zeroes, all
zeroes, all 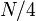 terminal ones, and
terminal ones, and 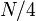 out of the
out of the 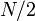 initial ones. Thus the output size is not polynomial in
initial ones. Thus the output size is not polynomial in  , and then neither can the algorithm be in the worst case.
, and then neither can the algorithm be in the worst case. 
However, this does not rule out the existence of a polynomial-time algorithm for the first two variations on the problem. We now present such an algorithm.
Algorithm
todo
References
- ↑ Jonathan T. Schneider (2010). Personal communication.
External links
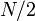 ones, followed by
ones, followed by 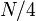 zeroes, and finally
zeroes, and finally 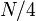 ones. (Assume
ones. (Assume  is a multiple of 4, although it does not really matter.) Any palindromic substring either does not contain any zeroes, in which case its length is only up to
is a multiple of 4, although it does not really matter.) Any palindromic substring either does not contain any zeroes, in which case its length is only up to 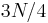 , or it contains at least one zero. If it contains at least one zero, it must be of the form
, or it contains at least one zero. If it contains at least one zero, it must be of the form 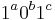 , but
, but 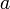 and
and 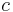 must be equal. (This is because the middle of the palindrome must lie somewhere within the zeroes, otherwise there would be no zeroes on one side of it and at least one zero on the other side; but as long as the middle lies within the zeroes, there must be an equal number of ones on each side.) But
must be equal. (This is because the middle of the palindrome must lie somewhere within the zeroes, otherwise there would be no zeroes on one side of it and at least one zero on the other side; but as long as the middle lies within the zeroes, there must be an equal number of ones on each side.) But 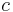 can only be up to
can only be up to 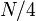 , and likewise with
, and likewise with 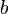 , so again the palindrome cannot be longer than
, so again the palindrome cannot be longer than 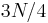 characters. However, there are
characters. However, there are 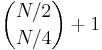 palindromic substrings of length
palindromic substrings of length 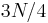 ; we can either take all the ones, or we can take all
; we can either take all the ones, or we can take all 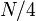 zeroes, all
zeroes, all 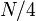 terminal ones, and
terminal ones, and 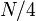 out of the
out of the 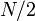 initial ones. Thus the output size is not polynomial in
initial ones. Thus the output size is not polynomial in  , and then neither can the algorithm be in the worst case.
, and then neither can the algorithm be in the worst case. 