Difference between revisions of "Naive algorithm"
(Created page with "An algorithm is said to be '''naive''' when it is simple and straightforward but does not exhibit a desirable level of efficiency (usually in terms of ...") |
|||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | An algorithm is said to be '''naive''' when it is simple and straightforward but does not exhibit a desirable level of [[Analysis of algorithms|efficiency]] (usually in terms of time, but also possibly memory) despite finding a correct solution or it does not find an optimal solution to an [[optimization problem]], and better algorithms can be designed and implemented with more careful thought and clever techniques. Naive algorithms are easy to discover, often easy to prove correct, and often immediately obvious to the problem solver. They are often based on simple [[simulation]] or on [[brute force]] generation of candidate solutions with little or no attempt at optimization. Despite their inefficiency, naive algorithms are often the stepping stone to more efficient, perhaps even asymptotically optimal algorithms, especially when their efficiency can be improved by choosing more appropriate [[data structure]]s. | + | An algorithm is said to be '''naive''' when it is simple and straightforward but does not exhibit a desirable level of [[Analysis of algorithms|efficiency]] (usually in terms of time, but also possibly memory) despite finding a correct solution or it does not find an optimal solution to an [[optimization problem]], and better algorithms can be designed and implemented with more careful thought and clever techniques. Naive algorithms are easy to discover, often easy to prove correct, and often immediately obvious to the problem solver. They are often based on simple [[simulation]] or on [[brute force]] generation of candidate solutions with little or no attempt at [[optimization]]. Despite their inefficiency, naive algorithms are often the stepping stone to more efficient, perhaps even asymptotically optimal algorithms, especially when their efficiency can be improved by choosing more appropriate [[data structure]]s. |
| − | For example, the naive algorithm for [[string searching]] entails trying to match the needle at every possible position in the haystack, doing an <math>O(m)</math> check at each step (where <math>m</math> is the length of the needle), giving an <math>O(mn)</math> runtime (where <math>n</math> is the length of the haystack). The realization that the check can be performed more efficiently using a hash function leads to the [[Rabin–Karp algorithm]]. The realization that preprocessing the needle can allow a failed attempt at matching to be used to rule out other possible positions leads to the [[Knuth–Morris–Pratt algorithm]]. The realization that preprocessing the haystack can allow needles to be "looked up" in the haystack rather than searched for in a linear fashion leads to the [[ | + | For example, the naive algorithm for [[string searching]] entails trying to match the needle at every possible position in the haystack, doing an <math>O(m)</math> check at each step (where <math>m</math> is the length of the needle), giving an <math>O(mn)</math> runtime (where <math>n</math> is the length of the haystack). The realization that the check can be performed more efficiently using a hash function leads to the [[Rabin–Karp algorithm]]. The realization that preprocessing the needle can allow a failed attempt at matching to be used to rule out other possible positions leads to the [[Knuth–Morris–Pratt algorithm]]. The realization that preprocessing the haystack can allow needles to be "looked up" in the haystack rather than searched for in a linear fashion leads to the [[suffix tree]] data structure which reduces string search to mere traversal. All of these algorithms are more efficient than the naive algorithm. |
[[Category:Algorithms]] | [[Category:Algorithms]] | ||
Latest revision as of 15:24, 29 June 2011
An algorithm is said to be naive when it is simple and straightforward but does not exhibit a desirable level of efficiency (usually in terms of time, but also possibly memory) despite finding a correct solution or it does not find an optimal solution to an optimization problem, and better algorithms can be designed and implemented with more careful thought and clever techniques. Naive algorithms are easy to discover, often easy to prove correct, and often immediately obvious to the problem solver. They are often based on simple simulation or on brute force generation of candidate solutions with little or no attempt at optimization. Despite their inefficiency, naive algorithms are often the stepping stone to more efficient, perhaps even asymptotically optimal algorithms, especially when their efficiency can be improved by choosing more appropriate data structures.
For example, the naive algorithm for string searching entails trying to match the needle at every possible position in the haystack, doing an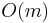 
check at each step (where 
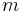is the length of the needle), giving an 
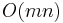runtime (where 
is the length of the haystack). The realization that the check can be performed more efficiently using a hash function leads to the Rabin–Karp algorithm. The realization that preprocessing the needle can allow a failed attempt at matching to be used to rule out other possible positions leads to the Knuth–Morris–Pratt algorithm. The realization that preprocessing the haystack can allow needles to be "looked up" in the haystack rather than searched for in a linear fashion leads to the suffix tree data structure which reduces string search to mere traversal. All of these algorithms are more efficient than the naive algorithm.
