Knuth–Morris–Pratt algorithm
The Knuth–Morris–Pratt (KMP) algorithm is a linear time solution to the single-pattern string search problem. It is based on the observation that a partial match gives useful information about whether or not the needle may partially match subsequent positions in the haystack. This is because a partial match indicates that some part of the haystack is the same as some part of the needle, so that if we have preprocessed the needle in the right way, we will be able to draw some conclusions about the contents of the haystack (because of the partial match) without having to go back and re-examine characters already matched. In particular, this means that, in a certain sense, we will want to precompute how the needle matches itself. The algorithm thus "never looks back" and makes a single pass over the haystack. Together with linear time preprocessing of the needle, this gives a linear time algorithm overall.
Contents
Motivation
The motivation behind KMP is best illustrated using a few simple examples.
Example 1
In this example, we are searching for the string  = aaa in the string
= aaa in the string  = aaaaaaaaa (in which it occurs seven times). The naive algorithm would begin by comparing
= aaaaaaaaa (in which it occurs seven times). The naive algorithm would begin by comparing 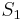 with
with 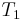 ,
, 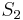 with
with 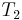 , and
, and 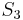 with
with 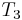 , and thus find a match for
, and thus find a match for  at position 1 of
at position 1 of  . Then it would proceed to compare
. Then it would proceed to compare 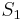 with
with 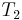 ,
, 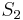 with
with 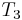 , and
, and 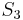 with
with 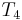 , and thus find a match at position 2 of
, and thus find a match at position 2 of  , and so on, until it finds all the matches. But we can do better than this, if we preprocess
, and so on, until it finds all the matches. But we can do better than this, if we preprocess  and note that
and note that 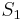 and
and 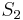 are the same, and
are the same, and 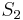 and
and 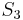 are the same. That is, the prefix of length 2 in
are the same. That is, the prefix of length 2 in  matches the substring of length 2 starting at position 2 in
matches the substring of length 2 starting at position 2 in  ;
;  partially matches itself. Now, after finding that
partially matches itself. Now, after finding that 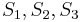 match
match 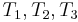 , respectively, we no longer care about
, respectively, we no longer care about 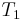 , since we are trying to find a match at position 2 now, but we still know that
, since we are trying to find a match at position 2 now, but we still know that 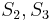 match
match 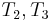 respectively. Since we already know
respectively. Since we already know 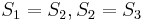 , we now know that
, we now know that 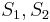 match
match 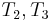 respectively; there is no need to examine
respectively; there is no need to examine 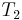 and
and 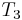 again, as the naive algorithm would do. If we now check that
again, as the naive algorithm would do. If we now check that 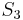 matches
matches 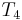 , then, after finding
, then, after finding  at position 1 in
at position 1 in  , we only need to do one more comparison (not three) to conclude that
, we only need to do one more comparison (not three) to conclude that  also occurs at position 2 in
also occurs at position 2 in  . So now we know that
. So now we know that 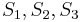 match
match 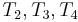 , respectively, which allows us to conclude that
, respectively, which allows us to conclude that 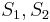 match
match 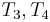 . Then we compare
. Then we compare 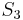 with
with 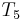 , and find another match, and so on. Whereas the naive algorithm needs three comparisons to find each occurrence of
, and find another match, and so on. Whereas the naive algorithm needs three comparisons to find each occurrence of  in
in  , our technique only needs three comparisons to find the first occurrence, and only one for each after that, and doesn't go back to examine previous characters of
, our technique only needs three comparisons to find the first occurrence, and only one for each after that, and doesn't go back to examine previous characters of  again. (This is how a human would probably do this search, too.)
again. (This is how a human would probably do this search, too.)
Example 2
Now let's search for the string  = aaa in the string
= aaa in the string  = aabaabaaa. Again, we start out the same way as in the naive algorithm, hence, we compare
= aabaabaaa. Again, we start out the same way as in the naive algorithm, hence, we compare 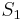 with
with 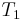 ,
, 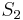 with
with 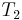 , and
, and 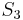 with
with 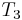 . Here we find a mismatch between
. Here we find a mismatch between  and
and  , so
, so  does not occur at position 1 in
does not occur at position 1 in  . Now, the naive algorithm would continue by comparing
. Now, the naive algorithm would continue by comparing 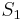 with
with 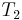 and
and 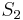 with
with 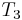 , and would find a mismatch; then it would compare
, and would find a mismatch; then it would compare 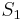 with
with 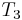 , and find a mismatch, and so on. But a human would notice that after the first mismatch, the possibilities of finding
, and find a mismatch, and so on. But a human would notice that after the first mismatch, the possibilities of finding  at positions 2 and 3 in
at positions 2 and 3 in  are extinguished. This is because, as noted in Example 1,
are extinguished. This is because, as noted in Example 1, 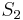 is the same as
is the same as 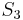 , and since
, and since 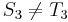 ,
, 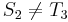 also (so we will not find
also (so we will not find  at position 2 of
at position 2 of  ). And, likewise, since
). And, likewise, since 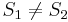 , and
, and 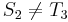 , it is also true that
, it is also true that 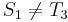 , so it is pointless looking for a match at the third position of
, so it is pointless looking for a match at the third position of  . Thus, it would make sense to start comparing again at the fourth position of
. Thus, it would make sense to start comparing again at the fourth position of  (i.e.,
(i.e., 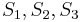 with
with 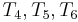 , respectively). Again finding a mismatch, we use similar reasoning to rule out the fifth and sixth positions in
, respectively). Again finding a mismatch, we use similar reasoning to rule out the fifth and sixth positions in  , and begin matching again at
, and begin matching again at 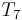 (where we finally find a match.) Again, notice that the characters of
(where we finally find a match.) Again, notice that the characters of  were examined strictly in order.
were examined strictly in order.
Example 3
As a more complex example, imagine searching for the string  = tartan in the string
= tartan in the string  = tartaric_acid. We make the observation that the prefix of length 2 in
= tartaric_acid. We make the observation that the prefix of length 2 in  matches the substring of length 2 in
matches the substring of length 2 in  starting from position 4. Now, we start by comparing
starting from position 4. Now, we start by comparing 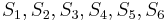 with
with 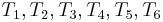 , respectively. We find that
, respectively. We find that 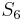 does not match
does not match 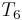 , so there is no match at position 1. At this point, we note that since
, so there is no match at position 1. At this point, we note that since 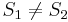 and
and 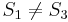 , and
, and 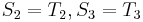 , obviously,
, obviously, 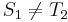 and
and 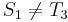 , so there cannot be a match at position 2 or position 3. Now, recall that
, so there cannot be a match at position 2 or position 3. Now, recall that 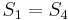 and
and 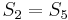 , and that
, and that 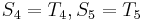 . We can translate this to
. We can translate this to 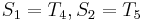 . So we proceed to compare
. So we proceed to compare 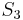 with
with 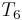 . In this way, we have ruled out two possible positions, and we have restarted comparing not at the beginning of
. In this way, we have ruled out two possible positions, and we have restarted comparing not at the beginning of  but in the middle, avoiding re-examining
but in the middle, avoiding re-examining 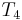 and
and 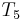 .
.
Concept
Let the prefix of length 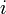 of string
of string  be denoted
be denoted 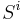 .
.
The examples above show that the KMP algorithm relies on noticing that certain substrings of the needle match or do not match other substrings of the needle, but it is probably not clear what the unifying organizational principle for all this match information is. Here it is:
- At each position
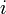 of
of  , find the longest proper suffix of
, find the longest proper suffix of 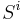 that is also a prefix of
that is also a prefix of  .
.
We shall denote the length of this substring by 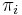 , following [1]. We can also state the definition of
, following [1]. We can also state the definition of 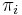 equivalently as the maximum
equivalently as the maximum 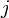 such that
such that  .
.
The table 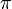 , called the prefix function, occupies linear space, and, as we shall see, can be computed in linear time. It contains all the information we need in order to execute the "smart" searching techniques described in the examples. In particular, in examples 1 and 2, we used the fact that
, called the prefix function, occupies linear space, and, as we shall see, can be computed in linear time. It contains all the information we need in order to execute the "smart" searching techniques described in the examples. In particular, in examples 1 and 2, we used the fact that 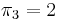 , that is, the prefix aa matches the suffix aa. In example 3, we used the facts that
, that is, the prefix aa matches the suffix aa. In example 3, we used the facts that 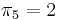 . This tells us that the prefix ta matches the substring ta ending at the fifth position. In general, the table
. This tells us that the prefix ta matches the substring ta ending at the fifth position. In general, the table 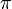 tells us, after either a successful match or a mismatch, what the next position is that we should check in the haystack. Comparison proceeds from where it was left off, never revisiting a character of the haystack after we have examined the next one.
tells us, after either a successful match or a mismatch, what the next position is that we should check in the haystack. Comparison proceeds from where it was left off, never revisiting a character of the haystack after we have examined the next one.
Computation of the prefix function
To compute the prefix function, we shall first make the following observation:
- Prefix function iteration lemma[1]: The sequence
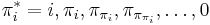 contains exactly those values
contains exactly those values 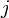 such that
such that  .
.
That is, we can enumerate all suffixes of 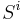 that are also prefixes of
that are also prefixes of  by starting with
by starting with 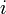 , looking it up in the table
, looking it up in the table 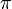 , looking up the result, looking up the result, and so on, giving a strictly decreasing sequence, terminating with zero.
, looking up the result, looking up the result, and so on, giving a strictly decreasing sequence, terminating with zero.
- Proof: We first show by induction that if
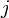 appears in the sequence
appears in the sequence 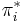 then
then  , i.e,
, i.e, 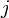 indeed belongs in the sequence
indeed belongs in the sequence 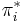 . Suppose
. Suppose 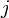 is the first entry in
is the first entry in 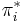 . Then
. Then 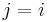 and it is trivially true that
and it is trivially true that  . Now suppose
. Now suppose 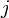 is not the first entry, but is preceded by the entry
is not the first entry, but is preceded by the entry 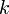 which is valid. That is,
which is valid. That is, 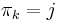 . By definition,
. By definition,  . But
. But  by assumption. Since
by assumption. Since  is transitive,
is transitive,  .
. - We now show by contradiction that if
 , then
, then 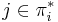 . Assume
. Assume 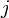 does not appear in the sequence. Clearly
does not appear in the sequence. Clearly 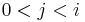 since 0 and
since 0 and 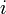 both appear. Since
both appear. Since 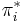 is strictly decreasing, we can find exactly one
is strictly decreasing, we can find exactly one 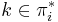 such that
such that 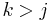 and
and 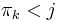 ; that is, we can find exactly one
; that is, we can find exactly one 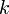 after which
after which 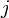 "should" appear (to keep the sequence decreasing). We know from the first part of the proof that
"should" appear (to keep the sequence decreasing). We know from the first part of the proof that  . Since the suffix of
. Since the suffix of 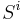 of length
of length 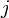 is a suffix of the suffix of
is a suffix of the suffix of 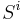 of length
of length 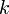 , it follows that the suffix of
, it follows that the suffix of 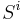 of length
of length 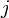 matches the suffix of length
matches the suffix of length 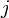 of
of 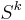 . But the suffix of
. But the suffix of 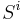 of length
of length 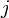 also matches
also matches 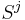 , so
, so 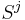 matches the suffix of
matches the suffix of 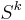 of length
of length 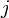 . We therefore conclude that
. We therefore conclude that 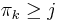 . But
. But 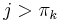 , a contradiction.
, a contradiction. 
With this in mind, we can design an algorithm to compute the table 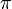 . For each
. For each 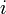 , we will first try to find some
, we will first try to find some 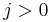 such that
such that  . If we fail to do so, we will conclude that
. If we fail to do so, we will conclude that 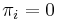 (clearly this is the case when
(clearly this is the case when 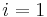 .) Observe that if we do find such
.) Observe that if we do find such 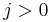 , then by removing the last character from this suffix, we obtain a suffix of
, then by removing the last character from this suffix, we obtain a suffix of 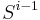 that is also a prefix of
that is also a prefix of  , i.e.,
, i.e.,  . Therefore, we first enumerate all nonempty proper suffixes of
. Therefore, we first enumerate all nonempty proper suffixes of 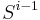 that are also prefixes of
that are also prefixes of  . If we find such a suffix of length
. If we find such a suffix of length 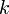 which also satisfies
which also satisfies 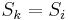 , then
, then 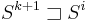 , and
, and 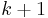 is a possible value of
is a possible value of 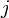 . So we will let
. So we will let 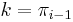 and keep iterating through the sequence
and keep iterating through the sequence 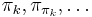 . We stop if we reach element
. We stop if we reach element 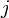 in this sequence such that
in this sequence such that 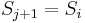 , and declare
, and declare 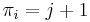 ; this always gives an optimal solution since the sequence
; this always gives an optimal solution since the sequence 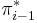 is decreasing and since it contains all possible valid
is decreasing and since it contains all possible valid 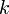 's. If we exhaust the sequence, then
's. If we exhaust the sequence, then 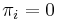 .
.
Here is the pseudocode:
π[1] ← 0
for i ∈ [2..m]
k ← π[i-1]
while k > 0 and S[k+1] ≠ S[i]
k ← π[k]
if S[k+1] = S[i]
π[i] ← 0
else
π[i] ← k+1
With a little bit of thought, this can be re-written as follows:
π[1] ← 0
k ← 0
for i ∈ [2..m]
while k > 0 and S[k+1] ≠ S[i]
k ← π[k]
if S[k+1] = S[i]
k ← k+1
π[i] ← k
This algorithm takes 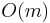 time to execute. To see this, notice that the value of
time to execute. To see this, notice that the value of k is never negative; therefore it cannot decrease more than it increases. It only increases in the line k ← k+1, which can only be executed up to 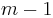 times. Therefore
times. Therefore k can be decreased at most k times. But k is decreased in each iteration of the while loop, so the while loop can only run a linear number of times overall. All the other instructions in the for loop take constant time per iteration, so linear time overall.
Matching
Suppose that we have already computed the table 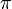 . Here's where we apply this hard-won information. Suppose that so far we are testing position
. Here's where we apply this hard-won information. Suppose that so far we are testing position 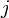 for a match, and that the first
for a match, and that the first 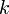 characters of
characters of  have been successfully matched, that is,
have been successfully matched, that is, 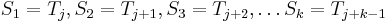 . There are two possibilities: either we just continue going along
. There are two possibilities: either we just continue going along  and
and  and comparing pairs of characters, or we decide we want to try out a new position in
and comparing pairs of characters, or we decide we want to try out a new position in  . This occurs because either
. This occurs because either 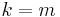 (i.e, we've successfully located
(i.e, we've successfully located  at position
at position 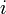 in
in  , and now we want to check out other positions) or because
, and now we want to check out other positions) or because 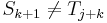 (so we can rule out the current position).
(so we can rule out the current position).
Given that 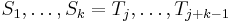 , what positions in
, what positions in  can we rule out? Here is the result at the core of the KMP algorithm:
can we rule out? Here is the result at the core of the KMP algorithm:
- Theorem: If
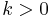 then
then 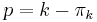 is the least
is the least 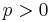 such that
such that 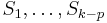 match
match 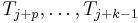 , respectively. (If
, respectively. (If 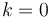 , then
, then 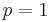 vacuously.)
vacuously.)
Think carefully about what this means. If 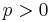 does not satisfy the statement that
does not satisfy the statement that 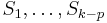 match
match 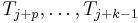 , then the needle
, then the needle  does not match
does not match  at position
at position 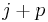 , i.e., we can rule out the position
, i.e., we can rule out the position 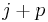 . On the other hand, if
. On the other hand, if 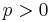 does satisfy this statement, then
does satisfy this statement, then  might match
might match  at position
at position 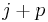 , and, in fact, all the characters up to but not including
, and, in fact, all the characters up to but not including 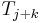 have already been verified to match the corresponding characters in
have already been verified to match the corresponding characters in  , so we can proceed by comparing
, so we can proceed by comparing 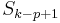 with
with 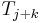 , and, as promised, never need to look back.
, and, as promised, never need to look back.
- Proof: Let
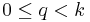 . If
. If  , then by definition we have
, then by definition we have 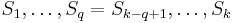 . But since
. But since 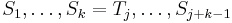 , it is also true that
, it is also true that 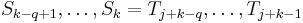 . Therefore
. Therefore 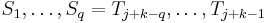 . If, on the other hand, it is not true that
. If, on the other hand, it is not true that  , then it is not true that
, then it is not true that 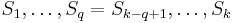 , so it is not true that
, so it is not true that 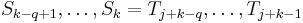 , so it is not true that
, so it is not true that 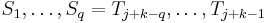 . Therefore
. Therefore 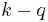 is a possible value of
is a possible value of 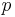 if and only if
if and only if  . Since the maximum possible value of
. Since the maximum possible value of 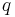 is
is 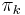 , the minimum possible value of
, the minimum possible value of 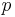 is given by
is given by 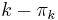 .
. 
Thus, here is the matching algorithm in pseudocode:
j ← 1
k ← 0
while j+m-1 ≤ n
while k ≤ m and S[k+1] = T[j+k]
k ← k+1
if k = m
print "Match at position " j
if k = 0
j ← j+1
else
j ← j+k-π[k]
k ← π[k]
Thus, we scan the text one character at a time; the current character being examined is located at position 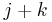 . When there is a mismatch, we use the
. When there is a mismatch, we use the 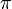 table to look up the next possible position at which the match might occur, and try to proceed.
table to look up the next possible position at which the match might occur, and try to proceed.
The fact that the algorithm scans one character at a time without looking back is more obvious when the code is cast into this equivalent form:[1]
k ← 0
for i ∈ [1..n]
while k > 0 and S[k+1] ≠ T[i]
k ← π[k]
if S[k+1] = T[i]
k ← k+1
if k = m
print "Match at position " i-m+1
k ← π[k]
Here, i is identified with j+k as above. Each iteration of the inner loop in one of these two segments corresponds to an iteration of the outer loop in the other. In this second form, we can also prove that the algorithm takes 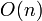 time; each time the inner while loop is executed, the value of
time; each time the inner while loop is executed, the value of k decreases, but it cannot decrease more than 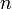 times because it starts as zero, is never negative, and is increased at most once per iteration of the outer loop (i.e., at most
times because it starts as zero, is never negative, and is increased at most once per iteration of the outer loop (i.e., at most 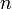 times in total), hence the inner loop is only executed up to
times in total), hence the inner loop is only executed up to 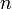 times. All other operations in the outer loop take constant time.
times. All other operations in the outer loop take constant time.
References
- ↑ 1.0 1.1 1.2 Thomas H. Cormen; Charles E. Leiserson, Ronald L. Rivest, Clifford Stein (2001). "Section 32.4: The Knuth-Morris-Pratt algorithm". Introduction to Algorithms (Second ed.). MIT Press and McGraw-Hill. pp. 923–931. ISBN 978-0-262-03293-3.