Difference between revisions of "Sliding range minimum query"
| Line 36: | Line 36: | ||
* {{Problem|ioi0612|IOI '06 - Pyramid}} | * {{Problem|ioi0612|IOI '06 - Pyramid}} | ||
* {{SPOJ|MATRIX2|Submatrix of Submatrix @ SPOJ}} | * {{SPOJ|MATRIX2|Submatrix of Submatrix @ SPOJ}} | ||
| + | |||
| + | [[Category:Pages needing code]] | ||
Revision as of 06:04, 10 June 2011
The sliding range minimum query is a special case of the static range minimum query that occurs when the query intervals are successive positions of a sliding window. That is, suppose that the query intervals are ![[a_1, b_1], [a_2, b_2], ..., [a_n, b_n]](/wiki/images/math/4/6/c/46c7762cfc306a393337755ab2ae1f62.png)
such that the 
's are increasing and the 
's are also increasing (in both cases, not necessarily strictly). This would be an instance of sliding range minimum query. This special case is important because it can be solved in linear time (that is, linear in the size of the array plus the number of query intervals) and requires no preprocessing. In particular, the algorithm will first find the range minimum for the leftmost query interval, then the second leftmost, and so on, and does not need to examine an element of the array until just before computing the minimum in the first query interval that actually contains this element; this means the results of earlier queries may be used to compute elements of the array and additional query intervals further to the right "on the fly".
First attempt
We start by assuming there is a data structure that will allow us to do three things efficiently:
- Insert a new element with a specified value.
- Remove an element with a specified value.
- Query the minimum value currently contained within.
Then, we could proceed by straightforward simulation; as we proceed from one position of the sliding window to the next, adding and removing elements, we add to and remove from the data structure the same elements, so that upon attaining a new position we can query the minimum element in the data structure and it will match the minimum element in the current interval.
It turns out that an ordered dynamic set will do insert and remove in logarithmic time and query in constant time. This gives a time bound of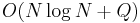 
where 
is the size of the array and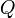 
is the number of query intervals, since no element will be inserted more than once or removed more than once. This solution is not asymptotically optimal, and it also has a large constant factor for the balanced binary search tree that is probably used to implement the set.
Refinement
To obtain a better solution, we begin by observing that the minimum can only decrease when a new element is added on the right and increase when an element is removed from the left:
- If a new element is added on the right and it is smaller than the current minimum, then the minimum decreases.
- When an element is removed from the left, the minimum will increase only if the removed element was the minimum.
Consider further what happens to the previous value in the first case: if a new element is added on the right and it is smaller than the current minimum, then the current minimum element will never be the minimum again. This is because it could only regain its status if the new element were removed, but it will itself be removed before the new element will (since it is further to the left.)
This leads us to formulate a Lemma.
Lemma: Suppose all elements of the array are distinct. Then, each element in the array will be the minimum either over a range of consecutive query intervals (i.e., for queries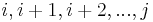 
and only those queries) or never at all.
Proof: Suppose element 
at index 
first becomes the minimum for query interval 
. Then, it will remain the minimum until either it is removed (in which case it will never be the minimum again) or until a smaller element is added (in which case, as explained above, again, it will never be the minimum again).
If the elements of the array are not distinct, a similar result still holds, assuming we have some way of breaking ties between elements with identical values (for example, the leftmost one is always considered the smallest).
The proof of the Lemma calls to mind two further observations:
- Whenever an element is ousted from its position as the minimum, it is always replaced by one further to the right.
- An element will never have a chance to be the minimum after a smaller element is added to its right.
Now, what if, whenever we add an element, we remove all the larger elements to its left? We can do this because those elements will never again be the minimum. If we do this, then our data structure will have the property that elements added later are always larger. This means the minimum element will always be the one added first. Furthermore, when this element is removed from the left as the sliding window moves, it is always the next oldest element that replaces it as the minimum.
We can now use a deque as our data structure, where most recently added elements are near the front and oldest elements near the back. When adding a new element on the right, first pop off all the larger elements from the front. When removing an old element from the left, simply pop it off the back. The element at the back will always be minimal. This gives the promised linear time bound without any precomputation.
