Difference between revisions of "Deque"
m (→Array implementation: fix pop_back(x) → pop_back) |
|||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | A '''deque''' is a data structure containing zero or more items, all of the same type, which may be thought to represent the items lined up in single file with a front and a back. It supports four basic operations: | + | A '''deque''' (pronounced /dɛk/ or /dik/) is a data structure containing zero or more items, all of the same type, which may be thought to represent the items lined up in single file with a front and a back. It supports four basic operations: |
* ''Push'' an element into the ''front'' of the deque. | * ''Push'' an element into the ''front'' of the deque. | ||
* ''Push'' an element into the ''back'' of the deque. | * ''Push'' an element into the ''back'' of the deque. | ||
| Line 14: | Line 14: | ||
These peek operations are not really necessary; ''peek front'' is the same as ''pop front'' followed by ''push front'', if the popped element is copied and then pushed back on; ''peek back'' can be defined analogously. And the ''test if empty'' operation is really a test of whether the result of the ''find size'' operation is zero. | These peek operations are not really necessary; ''peek front'' is the same as ''pop front'' followed by ''push front'', if the popped element is copied and then pushed back on; ''peek back'' can be defined analogously. And the ''test if empty'' operation is really a test of whether the result of the ''find size'' operation is zero. | ||
| − | =Terminology= | + | ==Terminology== |
The term ''deque'' is a shortened form of ''double-ended queue''. It is said to be double-ended because pushes and pops from both ends are possible; here the term ''queue'' is the name of a general class of data structures which allow insertion and removal of elements (but not search). The ''first'' element is the one at the front of the deque, and the ''last'' is the one at the back of the deque. An element can be described as ''before'' another if the former is closer to the front than the latter; the latter is referred to as being ''after'' the former. To ''push'' means to add an element, and to ''pop'' means to remove an element. Note that the front and the back of the deque are fully equivalent; we could interchange the terms ''front'' and ''back'' throughout our algorithms and they would work exactly as they did before. | The term ''deque'' is a shortened form of ''double-ended queue''. It is said to be double-ended because pushes and pops from both ends are possible; here the term ''queue'' is the name of a general class of data structures which allow insertion and removal of elements (but not search). The ''first'' element is the one at the front of the deque, and the ''last'' is the one at the back of the deque. An element can be described as ''before'' another if the former is closer to the front than the latter; the latter is referred to as being ''after'' the former. To ''push'' means to add an element, and to ''pop'' means to remove an element. Note that the front and the back of the deque are fully equivalent; we could interchange the terms ''front'' and ''back'' throughout our algorithms and they would work exactly as they did before. | ||
| − | =Implementation= | + | ==Implementation== |
===Array implementation=== | ===Array implementation=== | ||
In an array implementation of a deque, the contents of the deque are stored in consecutive indices in an array. However, we encounter a problem if we want the element in the lowest-indexed position (''i.e.'' 0 or 1) to be constantly at the front: when we pop from the front, we have to shift over all the other elements so that the lowest-indexed position contains the ''next'' element to be popped and all elements remain contiguous. The same applies if we want to push at the front; all elements currently in the deque would have to be shifted over to make room for the new element. These operations can both take <math>\mathcal{O}(N)</math> time where <math>N</math> is the number of elements currently in the deque. But we need [[Asymptotic analysis|constant time]] push/pop operations in order to make important algorithms like [[Breadth-first search|BFS]] run in linear time. To solve this, we do not replace the popped element, we merely increment an index into the next element to be popped, and we insert a pushed element at the index just before the current front element. That is, we maintain two indices into the array: one to the front and one to the back. When we push at the front, we add an element to the front and decrement the front index; when we push at the back, we add an element to the back and increment the back index; when we pop from the front, we remove the element from the front and increment the front index; when we pop from the back, we remove the element from the back and decrement the back index. However, consider what happens if, for example, we continually push one element at the front, then pop one from the back, then push another, and pop another, and so on: the size of the deque doesn't change much, but both indices will eventually go out of range. To fix this problem, we allow the indices to wrap around, so that incrementing the highest possible index will give the lowest possible one. This is done using the modulo operation. Following is an exemplary implementation: | In an array implementation of a deque, the contents of the deque are stored in consecutive indices in an array. However, we encounter a problem if we want the element in the lowest-indexed position (''i.e.'' 0 or 1) to be constantly at the front: when we pop from the front, we have to shift over all the other elements so that the lowest-indexed position contains the ''next'' element to be popped and all elements remain contiguous. The same applies if we want to push at the front; all elements currently in the deque would have to be shifted over to make room for the new element. These operations can both take <math>\mathcal{O}(N)</math> time where <math>N</math> is the number of elements currently in the deque. But we need [[Asymptotic analysis|constant time]] push/pop operations in order to make important algorithms like [[Breadth-first search|BFS]] run in linear time. To solve this, we do not replace the popped element, we merely increment an index into the next element to be popped, and we insert a pushed element at the index just before the current front element. That is, we maintain two indices into the array: one to the front and one to the back. When we push at the front, we add an element to the front and decrement the front index; when we push at the back, we add an element to the back and increment the back index; when we pop from the front, we remove the element from the front and increment the front index; when we pop from the back, we remove the element from the back and decrement the back index. However, consider what happens if, for example, we continually push one element at the front, then pop one from the back, then push another, and pop another, and so on: the size of the deque doesn't change much, but both indices will eventually go out of range. To fix this problem, we allow the indices to wrap around, so that incrementing the highest possible index will give the lowest possible one. This is done using the modulo operation. Following is an exemplary implementation: | ||
| Line 37: | Line 37: | ||
first = (first + 1) mod N | first = (first + 1) mod N | ||
return return_val | return return_val | ||
| − | function pop_back | + | function pop_back |
last = (last - 1) mod N | last = (last - 1) mod N | ||
return A[last] | return A[last] | ||
Latest revision as of 03:35, 4 March 2011
A deque (pronounced /dɛk/ or /dik/) is a data structure containing zero or more items, all of the same type, which may be thought to represent the items lined up in single file with a front and a back. It supports four basic operations:
- Push an element into the front of the deque.
- Push an element into the back of the deque.
- Pop an element from the front of the deque, returning its value in the process.
- Pop an element from the back of the deque, returning its value in the process.
In practice, we might choose to include the following operations as well:
- Construct an empty deque.
- Copy the contents of one deque to another.
- Peek at the front element in the deque, without removing it.
- Peek at the back element in the deque, without removing it.
- Empty an already existing deque.
- Find size of a deque.
- Test if empty.
These peek operations are not really necessary; peek front is the same as pop front followed by push front, if the popped element is copied and then pushed back on; peek back can be defined analogously. And the test if empty operation is really a test of whether the result of the find size operation is zero.
Contents
Terminology
The term deque is a shortened form of double-ended queue. It is said to be double-ended because pushes and pops from both ends are possible; here the term queue is the name of a general class of data structures which allow insertion and removal of elements (but not search). The first element is the one at the front of the deque, and the last is the one at the back of the deque. An element can be described as before another if the former is closer to the front than the latter; the latter is referred to as being after the former. To push means to add an element, and to pop means to remove an element. Note that the front and the back of the deque are fully equivalent; we could interchange the terms front and back throughout our algorithms and they would work exactly as they did before.
Implementation
Array implementation
In an array implementation of a deque, the contents of the deque are stored in consecutive indices in an array. However, we encounter a problem if we want the element in the lowest-indexed position (i.e. 0 or 1) to be constantly at the front: when we pop from the front, we have to shift over all the other elements so that the lowest-indexed position contains the next element to be popped and all elements remain contiguous. The same applies if we want to push at the front; all elements currently in the deque would have to be shifted over to make room for the new element. These operations can both take 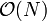 time where
time where  is the number of elements currently in the deque. But we need constant time push/pop operations in order to make important algorithms like BFS run in linear time. To solve this, we do not replace the popped element, we merely increment an index into the next element to be popped, and we insert a pushed element at the index just before the current front element. That is, we maintain two indices into the array: one to the front and one to the back. When we push at the front, we add an element to the front and decrement the front index; when we push at the back, we add an element to the back and increment the back index; when we pop from the front, we remove the element from the front and increment the front index; when we pop from the back, we remove the element from the back and decrement the back index. However, consider what happens if, for example, we continually push one element at the front, then pop one from the back, then push another, and pop another, and so on: the size of the deque doesn't change much, but both indices will eventually go out of range. To fix this problem, we allow the indices to wrap around, so that incrementing the highest possible index will give the lowest possible one. This is done using the modulo operation. Following is an exemplary implementation:
is the number of elements currently in the deque. But we need constant time push/pop operations in order to make important algorithms like BFS run in linear time. To solve this, we do not replace the popped element, we merely increment an index into the next element to be popped, and we insert a pushed element at the index just before the current front element. That is, we maintain two indices into the array: one to the front and one to the back. When we push at the front, we add an element to the front and decrement the front index; when we push at the back, we add an element to the back and increment the back index; when we pop from the front, we remove the element from the front and increment the front index; when we pop from the back, we remove the element from the back and decrement the back index. However, consider what happens if, for example, we continually push one element at the front, then pop one from the back, then push another, and pop another, and so on: the size of the deque doesn't change much, but both indices will eventually go out of range. To fix this problem, we allow the indices to wrap around, so that incrementing the highest possible index will give the lowest possible one. This is done using the modulo operation. Following is an exemplary implementation:
object deque
function construct(max_size)
let A be an array that can hold at least max_size+1 elements
let N = max_size+1
let first = 0
let last = 0
function push_front(x)
first = (first - 1) mod N
A[first] = x
function push_back(x)
A[last] = x
last = (last + 1) mod N
function pop_front
return_val = A[first]
first = (first + 1) mod N
return return_val
function pop_back
last = (last - 1) mod N
return A[last]
function peek_front
return A[first]
function peek_back
return A[(last-1) mod N]
function size
return (last-first) mod N
function make_empty
last = first
Notice that if the deque becomes full and we attempt to push more elements, then the apparent size will wrap to zero and some elements will be overwritten. Also, if we attempt to pop from an empty deque, the apparent size will wrap to the largest possible value. Error-checking code is fairly simple to add but, like the test if empty and copy operations, it has been omitted for the sake of brevity.
Linked list implementation
The circular array implementation will almost always be appropriate. However, for rare instances in which a contiguous block of memory of the required size cannot be found, a linked list can be used instead. Details of the list implementation are omitted below:
object deque
function construct
let L be an empty linked list
function push_front(x)
insert x before head of L
function push_back(x)
insert x after tail of L
function pop_front
remove head of L, returning its data element
function pop_back
remove tail of L, returning its data element
function peek_front
return data element at head of L
function peek_back
return data element at tail of L
function size
return size of L
function make_empty
empty L
As one can easily see, the deque is merely a container over the operations supported by the list itself. (Here we assume that the list maintains its own size; if this is not so then we can add a size field to the deque object.)
C++ STL deque class
In the C++ STL, std::deque, found in the <deque> header, is a template container capable of holding items of any (fixed) type, the type being supplied as a template argument. Hence, for example, deque<char> is a deque of characters. The container supplies the following member functions (note that T is the type of the elements of the deque):
-
void push_front(const T& x): pushesxinto the front of the deque. -
void push_back(const T& x): pushesxinto the back of the deque. -
void pop_front(): pops from the front of the deque. -
void pop_back(): pops from the back of the deque. -
T& front(): returns the element at the front of the deque -
T& back(): returns the element at the back of the deque -
size_type size(): returns the number of elements currently in the deque -
bool empty(): returnstrueif the deque is empty,falseotherwise. -
void clear(): removes all elements in the deque, leaving it empty.
Additionally, unlike the STL stack and queue containers, the deque container allows random-access iteration over its elements: hence D[0] is a reference to the element at the front of deque D, and so on.
The deque container should be used whenever it is sufficient for the problem at hand; it is quicker and less error-prone to use it than to code your own deque. You are highly unlikely to encounter an application for which the STL deque is too slow.
Note that the pop operations defined by this container are not identical to our own; they only remove the element and do not return its value. To do both, call front or back followed by pop_front or pop_back.
The STL stack and queue containers, except when this behavior is overridden by the corresponding template argument, are mere containers over STL deques; since the deque's behavior is a superset of the behaviors of the stack and queue, either can be obtained simply by manipulating a deque with a restricted set of operations.