Minimum spanning tree

A tree $T$ is said to span an undirected graph $G$ when $T$ is a subgraph of $G$ and contains all of $G$'s vertices. A minimum spanning tree is a spanning tree whose total edge weight is minimal. For example, suppose we model a network of computers with a graph. Each computer is a vertex and an edge exists between two computers if it is possible to wire them together; the weight of this edge is the cost required to do this. If we construct a spanning tree of the graph, and wire together two computers if and only if they are adjacent in the spanning tree, the network will be fully connected, that is, that any two computers in the network will be able to communicate. Finding a minimum spanning tree allows the computers to be networked together with minimum possible cost. (Note however that this system will have a single point of failure, and that real networks are designed to be more robust.)

Approaches to construction

We might try to construct a minimum spanning tree one vertex at a time. We start by picking any vertex in the graph; we know that this will have to be part of the minimum spanning tree. Then we pick the edge of lowest weight incident upon that vertex, as well as the edge's other endpoint; this now gives us two vertices connected by an edge. Then we consider all remaining edges that are incident upon either one of the vertices selected so far, and choose the one of lowest weight, and add it to our partially constructed tree along with its other endpoint, and so on; at each step we always select the lowest-weight edge that is incident upon one of the vertices so far selected and upon one not yet selected, and expand our partially built tree by one vertex and one edge. Eventually the graph will be exhausted and we will have a spanning tree. This technique is called Prim's algorithm, and it produces a minimum spanning tree.

Another approach is to build up the tree one edge at a time without regard to the connectivity of what we have so far. We sort the edges from lowest to highest weight then add them one by one to our partially built tree, except that we skip an edge if adding it would introduce a cycle. Eventually we will have added enough edges (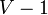$V-1$ of them); at this point, since there are still no cycles, we must have a tree that spans the graph (see tree article). This technique is called Kruskal's algorithm, and it generates a minimum spanning tree.

Another, older method is known as Boruvkå's algorithm.

Euclidean restriction

In some graphs, each vertex corresponds to a point in 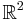$\mathbb{R}^2$ and an edge exists between every pair of vertices with weight equal to the 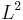$L^2$ (Euclidean) distance between the corresponding points. Finding a minimum spanning tree in this graph is known as the Euclidean minimum spanning tree problem. This can be solved using general minimum spanning tree algorithms, but this would take at least 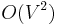$O(V^2)$ time because there are 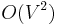$O(V^2)$ edges in the graph. A faster method, requiring only 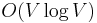$O(V \log V)$ time, is to construct the Delaunay triangulation of the set of points and then use an ordinary minimum spanning tree algorithm on this; it is guaranteed that a minimum spanning tree in the Delaunay triangulation is a minimum spanning tree of the original graph^{[proof needed]}. Since a Delaunay triangulation contains only 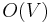$O(V)$ vertices, we get the stated time bound.