Edmonds–Karp algorithm
The Edmonds–Karp algorithm is a special case of the Ford–Fulkerson method that always chooses a shortest augmenting path at each iteration. It solves the maximum flow problem in 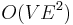 time.
time.
The algorithm
input flow network (V, s, t, c)
F ← 0
for u ∈ V
for v ∈ V
f[u, v] ← 0
r[u, v] ← c[u, v]
while t is reachable from s in (V, s, t, r)
find a shortest augmenting path (s = v[0], v[1], ..., v[n] = t) with BFS
m ← ∞
for i ∈ [0, n)
m ← min(m, r[v[i], v[i+1]])
for i ∈ [0, n)
f[v[i], v[i+1]] ← f[v[i], v[i+1]] + m
f[v[i+1], v[i]] ← f[v[i+1], v[i]] - m
r[v[i], v[i+1]] ← r[v[i], v[i+1]] - m
r[v[i+1], v[i]] ← r[v[i+1], v[i]] + m
F ← F + m
output max flow f
output max flow value F
Complexity
A trivial upper bound of 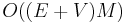 can be derived in the case that all edge capacities are integers. Each iteration of the algorithm uses breadth-first search, which takes
can be derived in the case that all edge capacities are integers. Each iteration of the algorithm uses breadth-first search, which takes 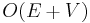 time, to find a shortest augmenting path, and there are at most
time, to find a shortest augmenting path, and there are at most 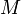 iterations, where
iterations, where 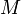 is the value of the max flow, since in each step the total flow so far increases by at least one unit.
is the value of the max flow, since in each step the total flow so far increases by at least one unit.
As a matter of fact, however, the Edmonds–Karp algorithm's running time has a capacity-independent bound, 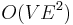 . The proof is not trivial and can be found in a textbook such as Introduction to Algorithms by Cormen et al.
. The proof is not trivial and can be found in a textbook such as Introduction to Algorithms by Cormen et al.