National Olympiad in Informatics, China, 1999

Day 1, Problem 3 - Birthday Cake

July 17^th is Mr. W's Birthday, and ACM-THU would like to create for him a birthday cake with volume Nπ, comprised of M cylindrical layers.

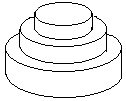
Counting upwards from the bottom layer, the i-th (1 ≤ i ≤ M) layer of cake is a cylinder with a radius of R_i and a height of H_i. When i < M, we require for R_i > R_i+1 and H_i > H_i+1.

To reduce the money spent on icing the cake, we would like to minimize Q, the outer surface area of the cake (not including the bottom surface of the bottommost layer).

Let Q = Sπ. Please write a program that, given N and M, finds a strategy to construct the cake (with appropriate R_i and H_i values) that minimizes the value of S.

Other than Q, all values described above will be positive integers.

Input Format

The input will consist of two lines. The first line is the integer N (N ≤ 10000), indicating that the volume of the cake is Nπ. The second line of input is the integer M (M ≤ 20), representing the number of levels in the cake.

Output Format

The output should consist of one line - a positive integer S (if no answer, S = 0).

Sample Input

100
2

Sample Output

68

Formulas for cylinders:

Volume: V = πR²H
Side surface area: A' = 2πRH
Bottom surface area: A = πR²

All Submissions
Best Solutions

Point Value: 20 (partial)
Time Limit: 1.00s
Memory Limit: 64M
Added: May 04, 2014

Languages Allowed:
C++03, PAS, C, HASK, ASM, RUBY, PYTH2, JAVA, PHP, SCM, CAML, PERL, C#, C++11, PYTH3

Comments (Search)