IOI '11 - Pattaya, Thailand
Race
In conjunction with the IOI, Pattaya City will host a race: the International Olympiad in Racing (IOR) 2011. As the host, we have to find the best possible course for the race.
In the Pattaya-Chonburi metropolitan area, there are N cities connected by a network of N-1 highways. Each highway is bidirectional, connects two different cities, and has an integer length in kilometers. Furthermore, there is exactly one possible path connecting any pair of cities. That is, there is exactly one way to travel from one city to another city by a sequence of highways without visiting any city twice.
The IOR has specific regulations that require the course to be a path whose total length is exactly K kilometers, starting and ending in different cities. Obviously, no highway (and therefore also no city) may be used twice on the course to prevent collisions. To minimize traffic disruption, the course must contain as few highways as possible.
Your Task
Write a program that takes the following parameters and finds the best path:
- N — the number of cities. The cities are numbered 0 through N-1.
- K — the required distance for the race course.
- H — a two-dimensional array representing highways. For 0 ≤ i < N-1, highway i connects the cities H[i][0] and H[i][1].
- L — a one-dimensional array representing the lengths of the highways. For 0 ≤ i < N-1, the length of highway i is L[i].
You may assume that all values in the array H are between 0 and N-1, inclusive, and that the highways described by this array connect all cities as described above. You may also assume that all values in the array L are integers between 0 and 1 000 000, inclusive.
Your program must output the minimum number of highways on a valid race course of length exactly K. If there is no such course, your program must output -1.
Examples
Example 1Consider the case shown in Figure 1, where N=4, K=3,
The course can start in city 0, go to city 1, and terminate in city 2. Its length will be exactly 1 km + 2 km = 3 km, and it consists of two highways. This is the best possible course; therefore the program must output 2. |
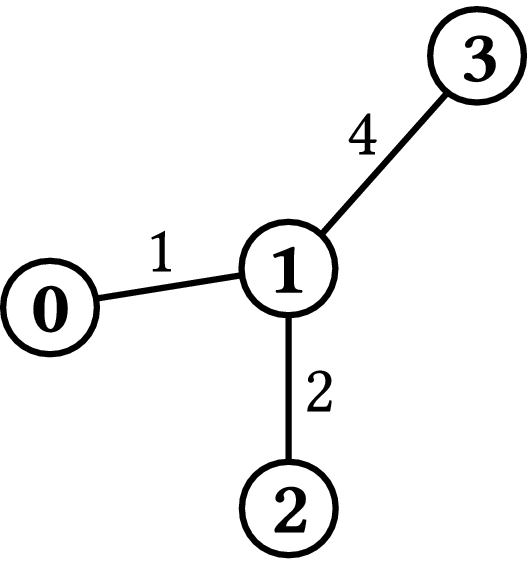
Figure 1.
|
Example 2Consider the case shown in Figure 2, where N=3, K=3,
There is no valid course. In this case, the program must output -1. |
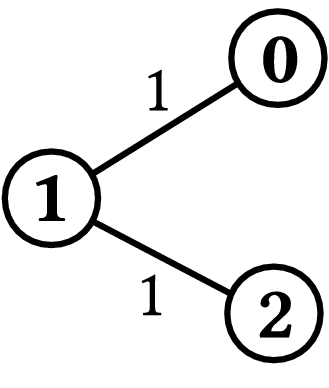
Figure 2.
|
Example 3Consider the case shown in Figure 3, where N=11, K=12,
One possible course consists of 3 highways: from city 6 via city 0 and city 2 to city 3. Another course starts in city 10 and goes via city 8 to city 6. Both of these courses have length exactly 12 km, as required. The second one is optimal, as there is no valid course with a single highway. Hence, the program must output 2. |
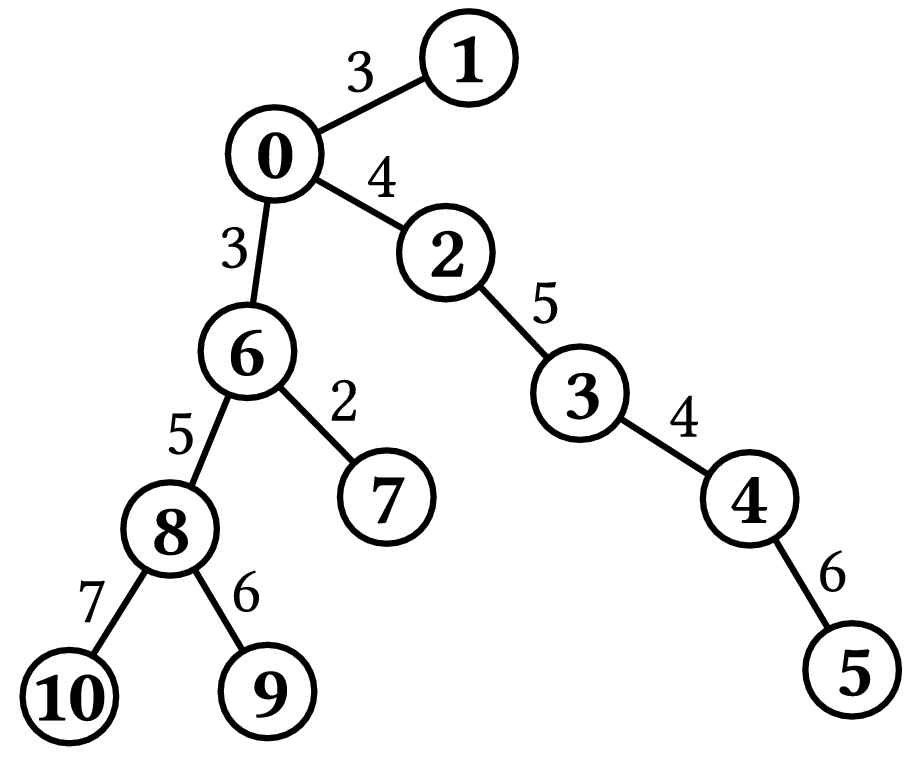
Figure 3.
|
Input Format
- Line 1: N and K
- Lines 2 to N: information on the highways; i.e., line i+2 contains H[i][0], H[i][1], and L[i], separated by a space, for 0 ≤ i < N-1.
Output Format
One integer, the expected solution.
Sample Input 14 3 0 1 1 1 2 2 1 3 4 Sample Output 12 |
Sample Input 23 3 0 1 1 1 2 1 Sample Output 2-1 |
Sample Input 311 12 0 1 3 0 2 4 2 3 5 3 4 4 4 5 6 0 6 3 6 7 2 6 8 5 8 9 6 8 10 7 Sample Output 32 |
Subtasks
Subtask 1 (9% of points)
- 1 ≤ N ≤ 100
- 1 ≤ K ≤ 100
- The network of highways forms the simplest possible line: For 0 ≤ i < N-1, highway i connects cities i and i+1.
Subtask 2 (12% of points)
- 1 ≤ N ≤ 1 000
- 1 ≤ K ≤ 1 000 000
Subtask 3 (22% of points)
- 1 ≤ N ≤ 200 000
- 1 ≤ K ≤ 100
Subtask 4 (57% of points)
- 1 ≤ N ≤ 200 000
- 1 ≤ K ≤ 1 000 000
All Submissions
Best Solutions
Point Value: 30 (partial)
Time Limit: 3.00s
Memory Limit: 256M
Added: Aug 24, 2013
Languages Allowed:
C++03, PAS, C, HASK, ASM, RUBY, PYTH2, JAVA, PHP, SCM, CAML, PERL, C#, C++11, PYTH3










Comments (Search)
It's quiet in here...