2013 Canadian Computing Competition, Stage 2
Day 2, Problem 1: A Romantic Movie Outing
Brian the Computer Science Nerd is going on a date with his girlfriend, Anatevka! His romantic location of choice is a movie theatre - but not an IMAX theatre, of course, as that would be far too expensive.
This theatre has 109 rows of 1000 seats each, which are initially
empty. The rows are numbered 1..109 starting from the one closest to
the screen, and the seats in each row are numbered 1..1000 from left to right.
Seat c in row r is denoted as seat
(r,c). Seats in rows 1..L
(1 ≤ L ≤ 1000) are considered to be
close
to the screen, while seats in further rows are considered to be
far
.
Over the course of T
(1 ≤ T ≤ 500000) minutes before the movie
starts, a number of events occur. During the ith minute,
either a person enters and sits in the empty seat
(Ri,Ci), the person sitting in the
occupied seat (Ri,Ci) leaves, or
Anatevka suggests that she and Brian take seats
(Ri,Ci) and
(Ri,Ci + 1). The type of
the ith event is represented by the character
Ei, with Ei = E
indicating a
person entering, Ei = L
indicating a person
leaving, and Ei = S
indicating a seating
suggestion. All seats involved in the events are valid seats inside the
theatre, and every seat that Anatevka suggests will be close
, as she
believes that they're the best.
Every time Anatevka makes a suggestion, Brian must, of course, analyze its
quality. If either of the two seats she suggests is already occupied, he should
explain that her recommendation is invalid with a simple No
. Otherwise,
he'd like to calculate the total inconvenience of both seats in such an
arrangement. The inconvenience of sitting in seat (r,c)
is the number of occupied seats in its field of vision (excluding itself). The
field of vision of seat (r,c) includes all seats which
are no further than it from seat (1,c) by Manhattan distance (i.e.,
Manhattan distance between
(x1, y1) and
(x2, y2) is
|x1 - x2| +
|y1 - y2|), as shown
below (with the S
representing a suggested seat, and an F
representing a seat within its field of vision):
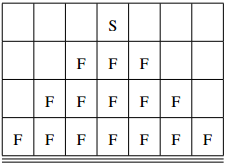
After all of the events have taken place, the movie is about to start, and a
final decision must be made on where to sit - and Brian will handle that. He
concludes that seats that are far
are clearly superior (as they offer a
broader view of the screen), and he knows that the point of going to the movies
is to have an optimal viewing experience, so selecting two adjacent seats is
certainly not mandatory. As such, he'd like to determine the minimum total
inconvenience for any two far
, unoccupied seats in the theatre. Note
that, if one of the chosen seats is in the other's field of vision, this does
not count towards its inconvenience - it's only determined by other people
sitting in the theatre.
Input
The first line of each test case contains two integers, L (1 ≤ L ≤ 1000) and T (1 ≤ T ≤ 500000).
The next T lines each contain one character, Ei (Ei ∈ {E, L, S}), and two integers, Ri and Ci, for i = 1..T (1 ≤ Ri ≤ 109; 1 ≤ Ci ≤ 1000).
For test cases worth 20% of the points, you may assume L ≤ 100 and T ≤ 400.
For test cases worth 60% of the points, you may assume L ≤ 500 and T ≤ 50000.
Output
For each of Anatevka's suggestions (i.e., when
Ei = S in the input), output the string
No if the suggestion is invalid; otherwise, output the total
inconvenience of the two suggested seats.
The last line of output should contain the minimum total inconvenience of
any pair of far
, unoccupied seats.
Sample Input
3 7 E 1 2 E 2 5 S 3 4 E 2 3 L 2 5 S 1 3 S 2 2
Sample Output
3 0 No 0
Explanation
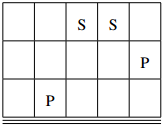
When Anatevka makes her first suggestion, the front 3 rows and leftmost 5
columns of the theatre look as follows (where a P
represents a person,
and an S
represents one of the suggested seats):
The person sitting in seat (1,2) is in the field of vision of both suggested seats, while the person sitting in seat (2,5) is only in the way of the right one. As such, the total inconvenience of the two seats is 1 + 2 = 3.
The second suggestion is shown below:
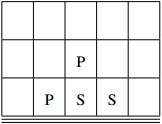
These two seats aren't obstructed by any people, so their total inconvenience is 0. The final suggestion is invalid, as one of its two seats (seat (2,3)) is already occupied.
Finally, Brian can easily select two far
seats which each have
inconvenience 0, as the theatre has 109 - 3 far
rows with 1000 seats each, and most are far from the two people setting in the
theatre after the last event. For example, he might choose to take seat (4,6),
while recommending that Anatevka enjoy the view from seat (100,1000).
All Submissions
Best Solutions
Point Value: 20 (partial)
Time Limit: 2.00s
Memory Limit: 128M
Added: May 19, 2013
Author: SourSpinach
Languages Allowed:
C++03, PAS, C, HASK, ASM, RUBY, PYTH2, JAVA, PHP, SCM, CAML, PERL, C#, C++11, PYTH3










Comments (Search)
This flawed data was indeed used at the CCC - this is my fault. However, looking at the full results, I believe it had no significant effect (and possibly none at all).