Prefix sum array and difference array
Given an array of numbers, we can construct a new array by replacing each element by the difference between itself and the previous element, except for the first element, which we simply ignore. This is called the difference array, because it contains the first differences of the original array. For example, the difference array of ![A = [9, 2, 6, 3, 1, 5, 0, 7]](/wiki/images/math/7/f/9/7f9d88c652b184dc4db1a19714f6dd80.png) is
is ![D = [2-9, 6-2, 3-6, 1-3, 5-1, 0-5, 7-0]](/wiki/images/math/9/5/b/95b0f63e7f767cff66dd83a9942272fa.png) , or
, or ![[-7, 4, -3, -2, 4, -5, 7]](/wiki/images/math/a/d/d/add580769fa99a870317b923383072b7.png) . Evidently, the difference array can be computed in linear time from the original array.
. Evidently, the difference array can be computed in linear time from the original array.
We can run this process in reverse: that is, given a difference array and the initial element of the original array, we can reconstruct the original array. To do this, we simply scan from left to right, and accumulate as we go along, giving ![[9, 9-7, 9-7+4, 9-7+4-3, 9-7+4-3-2, 9-7+4-3-2+4, 9-7+4-3-2+4-5, 9-7+4-3-2+4-5+7]](/wiki/images/math/3/f/5/3f592544414a398ffce16c37f7bfa3c1.png) . The reader should perform this calculation and confirm that this is indeed equal to
. The reader should perform this calculation and confirm that this is indeed equal to ![A = [9, 2, 6, 3, 1, 5, 0, 7]](/wiki/images/math/7/f/9/7f9d88c652b184dc4db1a19714f6dd80.png) . This reverse process can also be done in linear time, as each element in
. This reverse process can also be done in linear time, as each element in  is the sum of the corresponding element in
is the sum of the corresponding element in 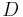 and the previous element in
and the previous element in  . We say that
. We say that  is a prefix sum array of
is a prefix sum array of 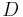 . However, it is not the only prefix sum array of
. However, it is not the only prefix sum array of 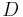 , because knowing
, because knowing 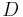 alone does not give us enough information to reconstruct
alone does not give us enough information to reconstruct  ; we also needed to know the initial element of
; we also needed to know the initial element of  . If we assumed that this were -3, for example, instead of 9, we would obtain
. If we assumed that this were -3, for example, instead of 9, we would obtain ![A' = [-3, -10, -6, -9, -11, -7, -12, -5]](/wiki/images/math/7/8/3/78383003eb80af422a06ec74ab48ca7d.png) .
. 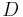 is the difference array of both
is the difference array of both  and
and 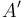 . Both
. Both  and
and 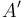 are prefix sum arrays of
are prefix sum arrays of 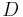 .
.
Analogy with calculus
These two processes—computing the difference array, and computing a prefix sum array—are the discrete equivalents of differentiation and integration in calculus, which operate on continuous domains:
- Differentiation and integration are reverses. Computing the difference array and computing a prefix sum array are reverses.
- A function can only have one derivative, but an infinite number of antiderivatives. An array has only one difference array, but an infinite number of prefix sum arrays.
- However, if we know the value of a function over an interval of the real line and we are given some real number, we can find one unique antiderivative of this function which attains this real value at the left end of the interval. Likewise, if we are given an array, and we are told the initial element of one of its prefix sum arrays, we can reconstruct the entire prefix sum array.
- When we take the difference array, we shorten the array by one element, since we destroy information about what the initial element was. On the other hand, when we take a prefix sum array, we lengthen the array by one element, since we introduce information about what the initial element is to be. Likewise, when we take the derivative of a function
![f:[a,b]\to\mathbb{R}](/wiki/images/math/3/3/2/332d0f0f6103ad3c4ec22d3af5b36e7c.png) on a closed interval, we obtain
on a closed interval, we obtain 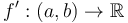 (open interval), and we destroy the information of what
(open interval), and we destroy the information of what 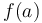 was; conversely, if we are given
was; conversely, if we are given 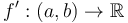 (open interval), and the value of
(open interval), and the value of 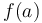 is also told to us, we obtain its antiderivative
is also told to us, we obtain its antiderivative ![f:[a,b]](/wiki/images/math/6/e/5/6e5363518c1d79fbdd1263e44c709ea3.png) (closed interval).
(closed interval). - All possible prefix sum arrays differ only by an offset from each other, in the sense that one of them can be obtained by adding a constant to each entry of the other. For example, the two prefix sum arrays shown for
 above differ by 12 at all positions. Likewise, all possible antiderivatives differ from each other only by a constant (the difference between their constants of integration).
above differ by 12 at all positions. Likewise, all possible antiderivatives differ from each other only by a constant (the difference between their constants of integration).
Because of these similarities, we will speak simply of differentiating and integrating arrays. An array can be differentiated multiple times, but eventually it will shrink to length 0. An array can be integrated any number of times. Differentiating 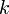 times and integrating
times and integrating 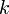 times are still reverse processes.
times are still reverse processes.
Use of prefix sum array
The Fundamental Theorem of Calculus also has an analogue, which is why the prefix sum array is so useful. If we assume both the original array and its prefix sum array are zero-indexed (or both one-indexed), for example, ![A = [9, 2, 6, 3, 1, 5, 0, 7]](/wiki/images/math/7/f/9/7f9d88c652b184dc4db1a19714f6dd80.png) where
where 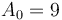 and
and ![P = [0, 9, 11, 17, 20, 21, 26, 26, 33]](/wiki/images/math/c/9/7/c97f7568d0b8ab4f0296a02102b114fb.png) (a possible prefix sum array of
(a possible prefix sum array of  , where we have arbitrarily chosen 0 as the initial element), where
, where we have arbitrarily chosen 0 as the initial element), where 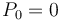 , then we can add up any range of elements in
, then we can add up any range of elements in  by taking the difference of two elements in
by taking the difference of two elements in  . In particular,
. In particular, 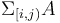 , the notation we will use for
, the notation we will use for 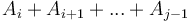 , is equal to
, is equal to  . (Note the use of the half-open interval.) For example,
. (Note the use of the half-open interval.) For example, 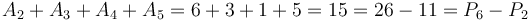 . This property holds no matter what we choose as the initial element of
. This property holds no matter what we choose as the initial element of  , because it will always cancel out of the calculation, just as we can use any antiderivative of a function to compute an integral (which is like summing a function across an entire interval) by taking the difference between the antiderivative's values at the endpoints, because the constant of integration will always cancel out. This makes the prefix sum array a useful item to precompute; once we have computed it, which only takes linear time, we can sum any range of the original array in constant time, simply by taking the difference of two values in the prefix sum array.
, because it will always cancel out of the calculation, just as we can use any antiderivative of a function to compute an integral (which is like summing a function across an entire interval) by taking the difference between the antiderivative's values at the endpoints, because the constant of integration will always cancel out. This makes the prefix sum array a useful item to precompute; once we have computed it, which only takes linear time, we can sum any range of the original array in constant time, simply by taking the difference of two values in the prefix sum array.
Example: Counting Subsequences (SPOJ)
Computing the prefix sum array is rarely the most difficult part of a problem. Instead, the prefix sum array is kept on hand because the algorithm to solve the problem makes frequent reference to range sums.
We will consider the problem Counting Subsequences from IPSC 2006. Here we are given an array of integers  and asked to find the number of contiguous subsequences of the array that sum to 47.
and asked to find the number of contiguous subsequences of the array that sum to 47.
To solve this, we will first transform array  into its prefix sum array
into its prefix sum array  . Notice that the sum of each contiguous subsequence
. Notice that the sum of each contiguous subsequence 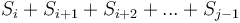 corresponds to the difference of two elements of
corresponds to the difference of two elements of  , that is,
, that is,  . So what we want to find is the number of pairs
. So what we want to find is the number of pairs 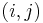 with
with 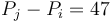 and
and 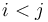 . (Note that if
. (Note that if 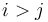 , we will instead get a subsequence with sum -47.)
, we will instead get a subsequence with sum -47.)
However, this is quite easy to do. We sweep through  from left to right, keeping a map of all elements of
from left to right, keeping a map of all elements of  we've seen so far, along with their frequencies; and for each element
we've seen so far, along with their frequencies; and for each element 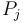 we count the number of times
we count the number of times  has appeared so far, by looking up that value in our map; this tells us how many contiguous subsequences ending at
has appeared so far, by looking up that value in our map; this tells us how many contiguous subsequences ending at 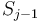 have sum 47. And finally, adding the number of contiguous subsequences with sum 47 ending at each entry of
have sum 47. And finally, adding the number of contiguous subsequences with sum 47 ending at each entry of  gives the total number of such subsequences in the array. Total time taken is
gives the total number of such subsequences in the array. Total time taken is 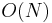 , if we use a hash table implementation of the map.
, if we use a hash table implementation of the map.