The Bellman-Ford algorithm finds single-source shortest paths in a directed, weighted graph which contains no negative-weight cycles. That is, unlike Dijkstra's algorithm, it is guaranteed to correctly compute shortest paths even when some edge weights are negative. (Note however that it is still a requirement that no negative-weight cycle occurs; finding shortest paths in such a graph becomes either meaningless if non-simple paths are allowed, or computationally difficult when they are not.) When single-source shortest paths are all that which is needed, and not all-pairs shortest paths, The Bellman–Ford algorithm, with time complexity 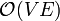$\mathcal{O}(VE)$ , outperforms the Floyd–Warshall algorithm at 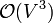$\mathcal{O}(V^3)$ in sparse graphs. It may also be combined with Dijkstra's algorithm to yield Johnson's algorithm, which again outperforms Floyd–Warshall in sparse graphs.

The algorithm

The idea behind the algorithm is very easy to understand, and may be satisfactorily illustrated by the following pseudocode:

input G,v
for each u ∈ V(G)
     let dist[u] = ∞
let dist[v] = 0
for each i ∈ [1..V-1]
     for each (u,w) ∈ E(G)
          dist[w] = min(dist[w],dist[u]+wt(u,w))
for each (u,w) ∈ E(G)
     if dist[w] > dist[u]+wt(u,w)
          error "Graph contains negative-weight cycles"

G is the directed, weighted graph in question, and v the source. The output is the array dist; at the completion of the algorithm, dist[x] contains the shortest-path distance from v to x. If the graph contains a cycle of negative weight, an error message is generated to that effect.

Theory of the algorithm

How the algorithm works

The algorithm works by performing a series of relaxations. A relaxation occurs whenever the current shortest distance from node v to node w is improved because, by travelling from v to some intermediate vertex u, and then from u to w, a shorter path is obtained. (Floyd–Warshall and Dijkstra's algorithms rely upon this same technique.) The key is that, after N passes of the main loop in Bellman–Ford have completed, at least N+1 of the shortest-path distances in dist are correct. (We consider all pairs of vertices to be connected, so that all "missing" edges are assigned a weight of positive infinity.)

Proof of correctness for graphs containing no negative-weight cycles

We proceed by induction:

When 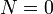$N=0$ , there is at least 1 correct entry in dist, the one stating that the distance from the source to itself is zero.
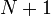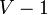Now suppose that $N$ passes have occurred and that we know the shortest-path distances from the source to $N+1$ of the vertices. Now, either $N$ is equal to $V-1$ , and we are done, or the vertices may be partitioned into two sets: $S$ , which contains 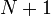$N+1$ vertices for which we already know shortest-path distances (with any 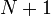$N+1$ being chosen if there are more than this number), and 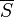$\overline{S}$ , which contains the rest. Now, since a shortest-paths tree exists (it always does when there are no negative-weight cycles; the proof is in the Shortest path article), there must exist some vertex w in 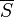$\overline{S}$ whose parent u in the shortest-paths tree is in $S$ . Then, when the edge (u,w) is relaxed, the dist array will contain the correct shortest-path distance to w. 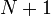Thus, after the next pass of the outer loop has occurred, $N+1$ passes will have occurred in total, and the shortest-path distances to at least 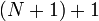$(N+1)+1$ vertices will be correctly known.

Thus, when a negative-weight cycle does not exist, after the main loop has finished, all distances in dist are correct. Now, if an edge (u,w) still exists such that dist[w] > dist[u]+wt(u,w), then the distances could not possibly have been correct, because relaxation of (u,w) would give a shorter path to w. Since this is a contradiction, the assumption of the non-existence of negative-weight cycles must be incorrect in this case. We see then that as long as there are no negative-weight cycles, the algorithm always computes all distances correctly and terminates successfully.

Proof of detection of negative-weight cycles

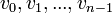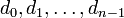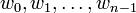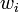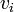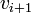Suppose vertices $v_0, v_1,..., v_{n-1}$ vertices form a negative-weight cycle, that at some point their entries in the dist array are $d_0, d_1,\ldots, d_{n-1}$ , and that the numbers $w_0, w_1,\ldots, w_{n-1}$ represent the weights of edges in the cycle, where $w_i$ is the weight of the edge from $v_i$ to $v_{i+1}$ . Now, because the cycle has negative weight, we know that 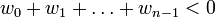$w_0+w_1+\ldots+w_{n-1}<0$ . We show by contradiction that it is always possible to relax one of the edges.

Suppose we assume the opposite: that there exists no 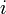$i$ such that 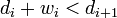$d_i + w_i < d_{i+1}$ . Then, we have 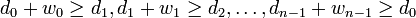$d_0 + w_0 \ge d_1, d_1 + w_1 \ge d_2,\ldots, d_{n-1} + w_{n-1} \ge d_0$ . Adding yields 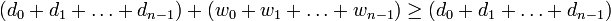$(d_0 + d_1 + \ldots + d_{n-1}) + (w_0 + w_1 + \ldots + w_{n-1}) \ge (d_0 + d_1 + \ldots + d_{n-1})$ , which, after cancelling the 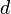$d$ 's, is a contradiction. So our assumption must be false, and it must always be possible to relax at least one of the edges in a negative-weight cycle. Thus, if there is a negative-weight cycle, it will always be detected at the end of the algorithm, because at least one edge on that cycle must be capable of relaxation.