Tree/Proof of properties of trees
Theorem: For a simple graph, any two of these three statements, taken together, imply the third:
- The graph is connected.
- The graph is acyclic.
- The number of vertices in the graph is exactly one more than the number of edges.
Proof: By induction. In a graph with one vertex, all three statements hold, so the claim is trivially true. Now suppose that the claim holds for all simple graphs with 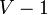 vertices (where
vertices (where 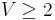 ). We show it holds for all graphs with
). We show it holds for all graphs with 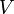 vertices:
vertices:
- Suppose a simple graph
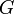 has
has 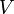 vertices and it is connected and acyclic. Choose any vertex
vertices and it is connected and acyclic. Choose any vertex  . Clearly
. Clearly  has degree at least one, since the graph is connected. If
has degree at least one, since the graph is connected. If  has degree one, stop. If not, choose any edge incident upon
has degree one, stop. If not, choose any edge incident upon  and denote the other endpoint
and denote the other endpoint  . If
. If  has degree one, stop; otherwise choose a different edge out of
has degree one, stop; otherwise choose a different edge out of  and denote the other endpoint
and denote the other endpoint 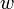 ; keep following this procedure until reaching a vertex of degree one. (This procedure must terminate, otherwise the vertices of the graph would be exhausted and a cycle would be formed, a contradiction.) Let
; keep following this procedure until reaching a vertex of degree one. (This procedure must terminate, otherwise the vertices of the graph would be exhausted and a cycle would be formed, a contradiction.) Let 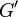 be
be 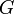 minus this vertex and its single incident edge. Clearly
minus this vertex and its single incident edge. Clearly 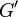 is still connected and acyclic and has
is still connected and acyclic and has 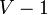 vertices; therefore it has
vertices; therefore it has 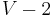 edges by the inductive hypothesis. Therefore
edges by the inductive hypothesis. Therefore 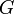 has
has 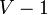 edges.
edges. - Suppose a simple graph
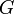 has
has 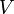 vertices, is connected, and has
vertices, is connected, and has 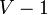 edges. Since the graph is connected, all vertices have degree at least one. If every vertex has degree at least two, then the sum of degrees is at least
edges. Since the graph is connected, all vertices have degree at least one. If every vertex has degree at least two, then the sum of degrees is at least 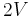 , so, by the handshake lemma, there are at least
, so, by the handshake lemma, there are at least 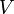 vertices, a contradiction; therefore at least one vertex must have degree one. Let
vertices, a contradiction; therefore at least one vertex must have degree one. Let 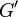 be the graph obtained by removing this vertex and its incident edge from
be the graph obtained by removing this vertex and its incident edge from 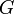 . Then
. Then 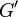 is still connected and it has
is still connected and it has 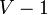 vertices and
vertices and 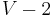 edges; by the inductive hypothesis, it is acyclic. Adding a single vertex and connecting it via a single edge to regenerate
edges; by the inductive hypothesis, it is acyclic. Adding a single vertex and connecting it via a single edge to regenerate 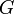 clearly does not introduce any cycles.
clearly does not introduce any cycles. - Suppose a simple graph
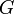 is acyclic and has
is acyclic and has 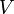 vertices and
vertices and 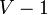 edges. Assume
edges. Assume 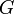 is not connected. Then, partition
is not connected. Then, partition 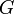 into two nonempty subgraphs
into two nonempty subgraphs 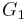 and
and 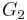 (with
(with 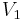 and
and 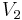 vertices, respectively) such that there are no edges in
vertices, respectively) such that there are no edges in 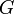 between vertices from
between vertices from 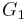 and
and 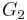 . Clearly both
. Clearly both 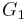 and
and 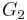 are acyclic. If
are acyclic. If 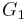 has at most
has at most 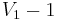 edges and
edges and 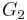 has at most
has at most 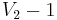 edges, then
edges, then 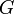 has at most
has at most 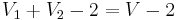 edges, a contradiction. Therefore, without loss of generality, assume
edges, a contradiction. Therefore, without loss of generality, assume 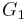 has at least
has at least 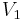 edges. Since
edges. Since 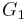 is acyclic, the graph
is acyclic, the graph 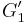 obtained by removing enough edges from
obtained by removing enough edges from 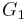 so that there are only
so that there are only 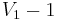 edges left is also acyclic. Now, by the inductive hypothesis,
edges left is also acyclic. Now, by the inductive hypothesis, 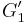 is connected. Therefore, if we add any edge to
is connected. Therefore, if we add any edge to 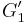 it will join two vertices that are already connected, and thus form a cycle. Therefore
it will join two vertices that are already connected, and thus form a cycle. Therefore 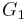 is not acyclic, a contradiction.
is not acyclic, a contradiction.

Proposition: There exists exactly one simple path between each pair of vertices in any tree.
Proof: A tree is connected, therefore there exists at least one simple path between each pair of vertices. Suppose there exist two simple paths (or more) between the vertices  and
and  , with
, with 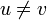 , namely,
, namely, 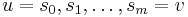 and
and 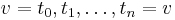 . Let
. Let 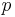 be the least
be the least 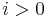 such that
such that 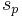 equals one of the
equals one of the 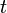 's. Clearly such a
's. Clearly such a 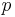 always exists because
always exists because 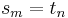 and
and 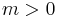 . Let
. Let 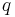 be such that
be such that 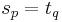 ; since both paths are simple, there is exactly one such
; since both paths are simple, there is exactly one such 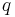 . Then consider the sequence of vertices
. Then consider the sequence of vertices 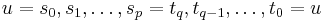 . Clearly no two of the
. Clearly no two of the  's are equal, since they are drawn from a simple path; the same is true of the
's are equal, since they are drawn from a simple path; the same is true of the 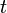 's. Also,
's. Also, 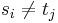 unless
unless 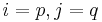 or
or 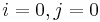 , because of the way
, because of the way 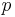 was selected. Therefore this sequence of vertices forms a simple cycle, a contradiction.
was selected. Therefore this sequence of vertices forms a simple cycle, a contradiction.

Proposition: Every tree is planar.
Proof 1: Since 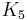 and
and 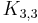 are not acyclic, neither are any of their subdivisions. Therefore no subdivision of either of these is a subgraph of any tree, as all subgraphs of any tree are acyclic. By Kuratowski's theorem, all trees are therefore planar.
are not acyclic, neither are any of their subdivisions. Therefore no subdivision of either of these is a subgraph of any tree, as all subgraphs of any tree are acyclic. By Kuratowski's theorem, all trees are therefore planar.
Proof 2: It is not difficult to devise an algorithm to generate a planar embedding of a tree. The details are left as an exercise to the reader.

Theorem: In a binary tree with external path length 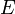 , internal path length
, internal path length 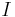 , and
, and  nodes,
nodes, 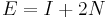 . (Caution: the statement
. (Caution: the statement 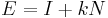 for
for 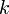 -ary trees is not, in general, true.)
-ary trees is not, in general, true.)
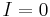 ,
, 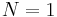 , and
, and 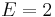 , since the root potentially has two children, each at depth 1. Thus,
, since the root potentially has two children, each at depth 1. Thus, 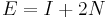 , as expected. Now, assume that
, as expected. Now, assume that 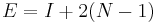 for all binary trees of
for all binary trees of 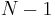 vertices, where
vertices, where 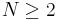 . Then, consider a binary tree
. Then, consider a binary tree  of
of  vertices. Choose a leaf of this tree and suppose it is at depth
vertices. Choose a leaf of this tree and suppose it is at depth 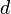 . Remove this from
. Remove this from  to give the tree
to give the tree 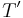 with
with 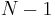 vertices, internal path length
vertices, internal path length 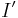 , external path length
, external path length 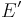 , and
, and 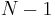 nodes. The removal of the leaf node of depth
nodes. The removal of the leaf node of depth 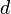 decreases the internal path length by
decreases the internal path length by 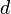 , so
, so 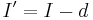 . It also removes two external nodes of depth
. It also removes two external nodes of depth 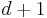 , which decreases the external path length by
, which decreases the external path length by 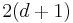 . But it introduces an external node of depth
. But it introduces an external node of depth 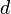 (where the leaf formerly was), which increases the external path length by
(where the leaf formerly was), which increases the external path length by 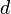 , so
, so 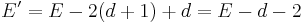 . By the inductive hypothesis,
. By the inductive hypothesis, 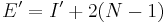 . Therefore
. Therefore 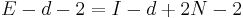 , so
, so 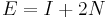 .
.