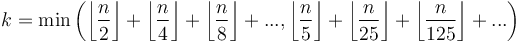Trailing zeroes in factorial
A well-known programming exercise involves finding the number of trailing zeroes at the end of the decimal representation of 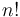 , for some given value of
, for some given value of  .[1][2]
.[1][2]
One possible approach, of course, is to explicitly calculate the factorial. The only problem with this is that 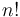 may be very large for reasonably sized values of
may be very large for reasonably sized values of  . For example,
. For example, 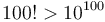 , so bignum arithmetic is needed for this kind of approach. This tends to be slow and inexpedient.
, so bignum arithmetic is needed for this kind of approach. This tends to be slow and inexpedient.
A much cleverer solution—one that does not involve calculating the factorial explicitly—can be obtained by noting that what is really desired is the largest  such that
such that 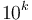 divides
divides 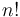 . The prime factorization of
. The prime factorization of 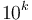 is
is 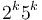 , so really all we need to do is find out how many factors of 2 are in
, so really all we need to do is find out how many factors of 2 are in 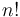 , and how many factors of 5 are in
, and how many factors of 5 are in 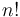 , and the smaller of the two gives the answer. For example,
, and the smaller of the two gives the answer. For example, 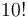 has prime factorization
has prime factorization 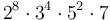 , so it contains 8 factors of 2 and 2 factors of 5. Consistent with these figures, there are 2 zeroes at the end of its decimal representation (3628800).
, so it contains 8 factors of 2 and 2 factors of 5. Consistent with these figures, there are 2 zeroes at the end of its decimal representation (3628800).
How do we calculate this? A workable approach is to simply determine how many factors of 2 and 5 are in each of the numbers 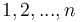 . When we multiply those numbers to get
. When we multiply those numbers to get 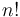 , we of course add the exponents in their prime factorizations; so the sum of the numbers of factors of 2 in each of the integers
, we of course add the exponents in their prime factorizations; so the sum of the numbers of factors of 2 in each of the integers 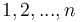 gives us the number of factors of 2 in
gives us the number of factors of 2 in 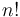 ; and we do something similar for factors of 5. Determining how many times 2 or 5 divides a number is as easy as actually performing the division over and over again (until a non-integer result is obtained).
; and we do something similar for factors of 5. Determining how many times 2 or 5 divides a number is as easy as actually performing the division over and over again (until a non-integer result is obtained).
There is a cleverer solution yet, though. When we multiply all the numbers from 1 to  , exactly
, exactly 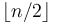 of them will be even, so each one of those contributes a factor of 2. However, the ones that are divisible by 4 actually contribute two factors of 2, so we have to add
of them will be even, so each one of those contributes a factor of 2. However, the ones that are divisible by 4 actually contribute two factors of 2, so we have to add 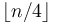 to the result (we counted those numbers once in
to the result (we counted those numbers once in 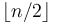 , and now we are counting them again in
, and now we are counting them again in 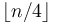 ). But then there may be some numbers that are divisible by 8, which contribute at least three factors of 2, so we have to add
). But then there may be some numbers that are divisible by 8, which contribute at least three factors of 2, so we have to add 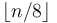 ; and so on until we reach some power of 2 that is greater than
; and so on until we reach some power of 2 that is greater than  (so that it obviously divides none of
(so that it obviously divides none of 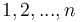 ). We can then do something similar for factors of 5. This gives us a formula:
). We can then do something similar for factors of 5. This gives us a formula:
It is now fairly obvious by inspection that the second argument—the number of factors of 5—is always the smaller of the two.
This formula can be used as-is, hence:
#include <stdio.h> int main() { int n; scanf("%d", &n); int p = 5; int k = 0; while (p <= n) { k += n/p; p *= 5; } printf("There are %d zeroes at the end of %d!\n", k, n); return 0; }
The formula can also be re-worked into the following form. The mathematical reasoning behind the correctness of this implementation is left as an exercise for the reader.
#include <stdio.h> int main() { int n; scanf("%d", &n); int k = 0; while (n > 0) k += n /= 5; printf("There are %d zeroes at the end of %d!\n", k, n); return 0; }
Functional style (Haskell):
zeroes = sum . tail . takeWhile (>0) . iterate (flip div 5) -- note that 0 is an edge case
Bases other than 10 may be trickier to handle. For example, consider the problem of finding the number of zeroes at the end of 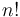 when expressed in base 12 (with prime factorization
when expressed in base 12 (with prime factorization 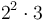 ). In this case we have to count factors of 2 and factors of 3, but it takes two factors of 2 to make one factor of 12, so we have to divide by two and then compare it with the number of factors of 3 (the smaller of the two results will be the answer). It's not obvious which factor will "run out" first, so it might be necessary to find the number of times each prime factor in the base appears in
). In this case we have to count factors of 2 and factors of 3, but it takes two factors of 2 to make one factor of 12, so we have to divide by two and then compare it with the number of factors of 3 (the smaller of the two results will be the answer). It's not obvious which factor will "run out" first, so it might be necessary to find the number of times each prime factor in the base appears in 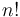 . The algorithm shown above still works for each individual prime factor, though (provided that "5" is replaced with the appropriate number).
. The algorithm shown above still works for each individual prime factor, though (provided that "5" is replaced with the appropriate number).