Ternary search
Ternary search is an algorithm similar to binary search. It is used when we have a function that is bitonic on a given interval instead of monotone, and we wish to optimize its value on that interval. That is, either the function first increases and then decreases, and we wish to find its maximum (that is, where it changes from increasing to decreasing), or it first decreases and then increases, and we wish to find the minimum. (In the former case, finding the minimum is trivial; it is at either the left edge or the right edge of the interval. In the latter case, finding the maximum is trivial.)
For the algorithm to work, we need the increase and decrease to be strict. Otherwise, we could have a pathological case in which the function is constant at all but one point, and then it would be impossible to find that point in the continuous case (and would be impossible to do it efficiently in the discrete case).
Should we wish to find a specific value, we can use binary search on the increasing part and the decreasing part separately, after having located the extremum and hence determined where the increasing part and decreasing part begin and end.
The function in question is usually defined on a continuous domain rather than a discrete domain, which gives the following pseudocode for the increasing-then-decreasing case:
// a: left edge of interval
// b: right edge of interval
// f: function
// epsilon: tolerance
input a, b, f, epsilon
l ← a
r ← b
while (r-l > epsilon)
m1 ← (2*l + r)/3
m2 ← (l + 2*r)/3
if f(m1) < f(m2)
l ← m1
else
r ← m2
print r
The reasoning is as follows. We split the interval ![[l, r]](/wiki/images/math/a/6/1/a615eebe867a499ba18a5de92492cf93.png) into three equal subintervals:
into three equal subintervals: ![[l, m_1]](/wiki/images/math/f/5/1/f51fcc9dded6415b0767b0b24f74aa4d.png) ,
, ![[m_1, m_2]](/wiki/images/math/b/9/6/b96503f0c7960acd1c9c19a5d2d18a24.png) , and
, and ![[m_2, r]](/wiki/images/math/2/8/8/288f8cf6e84b4e5f95477b49ead82ae0.png) . Then we evaluate
. Then we evaluate  at the intermediate points
at the intermediate points 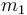 and
and 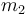 . We then consider the result of the comparison:
. We then consider the result of the comparison:
- If
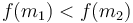 , then the maximum can't possibly occur in the first interval, since then the function would be increasing from
, then the maximum can't possibly occur in the first interval, since then the function would be increasing from 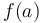 to the maximum, then decreasing from the maximum to
to the maximum, then decreasing from the maximum to 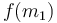 , and then at some point increasing again since
, and then at some point increasing again since 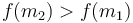 . So we discard the first interval.
. So we discard the first interval. - If
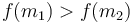 , then the maximum can't possibly occur in the third interval, by similar reasoning.
, then the maximum can't possibly occur in the third interval, by similar reasoning. - If
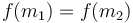 , then the maximum has to be in the second interval; if it were in the first interval then the function would not be strictly decreasing afterward, and if it were in the third interval then the function would not be strictly increasing at the beginning. Here, we can either discard the first or the third interval; it doesn't matter which. That's why we don't need a case in the code for this case.
, then the maximum has to be in the second interval; if it were in the first interval then the function would not be strictly decreasing afterward, and if it were in the third interval then the function would not be strictly increasing at the beginning. Here, we can either discard the first or the third interval; it doesn't matter which. That's why we don't need a case in the code for this case.
Intuitively, evaluating the function at the two intermediate points tips us off as to which "direction" to look in, as though we are climbing a hill. When the function is higher at the first than at the second, we know the maximum lies in one of the two left subintervals, and when it is higher at the second than at the first, we know the maximum lies in one of the two right subintervals. If the bitonicity is not strict, then we might not be able to obtain any useful information from the comparison, so this is not allowed.
The loop runs about 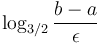 times, since each iteration reduces the length of the interval
times, since each iteration reduces the length of the interval ![[l,r]](/wiki/images/math/a/6/1/a615eebe867a499ba18a5de92492cf93.png) by a factor of
by a factor of 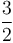 . Each iteration involves two evaluations of the function, so the total number of evaluations is about
. Each iteration involves two evaluations of the function, so the total number of evaluations is about 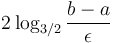 . This is
. This is 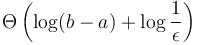 , so the smaller the epsilon, the longer the search takes, but overall the time is logarithmic in the length of the initial interval.
, so the smaller the epsilon, the longer the search takes, but overall the time is logarithmic in the length of the initial interval.
An example application of ternary search is finding a point 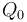 on a line segment
on a line segment 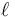 such that the distance
such that the distance 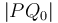 is minimal (where point
is minimal (where point  is given). Although there is a direct mathematical solution to this problem, an easier solution that allows us to approximate
is given). Although there is a direct mathematical solution to this problem, an easier solution that allows us to approximate 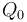 is to parameterize the line segment: let
is to parameterize the line segment: let 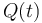 be the point on the line segment that is a distance
be the point on the line segment that is a distance  from one of the endpoints, and then notice that
from one of the endpoints, and then notice that 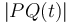 is a bitonic function whose minimum we wish to find (this can easily be proven using the Pythagorean theorem). Thus, ternary search can be used to find the point. Intuitively, we divide the line segment into thirds, and measure the distance from
is a bitonic function whose minimum we wish to find (this can easily be proven using the Pythagorean theorem). Thus, ternary search can be used to find the point. Intuitively, we divide the line segment into thirds, and measure the distance from  to each of the two dividing points, thus discarding one third of the segment, and repeating as far as necessary.
to each of the two dividing points, thus discarding one third of the segment, and repeating as far as necessary.