Sliding window
A sliding window is an interval both of whose endpoints are allowed to move only forward, and never backward (or vice versa). It is analogous to an actual window that opens from left to right; when opening the window its left edge only moves to the right, and so does its right edge, and when closing it, the opposite is true.
However, in computer science, sliding windows are allowed to change in size as they are moving; the right edge may move without the left edge's movement, or vice versa. Notice that when the right edge moves, the window becomes larger, and when the left edge moves, the window becomes smaller.
The sliding window is used in certain situations in which we need to keep track of some function whose domain is the set of intervals, with the property that the function's value can be efficiently recomputed after one of the edges moves a small amount.
A simple example is as follows: given a list of non-negative integers, we wish to find the longest interval (contiguous subsequence of the list) with the property that the sum of all the elements it contains does not exceed a bound 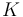 .
.
To solve this problem, we first observe that if we know the sum of all the elements in an interval, and we advance the left edge of the interval, then we simply exclude one element from the old interval from the new interval, and the sum decreases by the value of that element; and if we advance the right edge, then we simply include one new element, and the sum increases by the value of that element.
We then observe that for every possible position of the left edge of an interval, there is a corresponding position of the right edge such that the resulting interval is the longest interval possible with its left edge at the given position such that its sum does not exceed 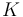 . For example, if the array is given by
. For example, if the array is given by ![[9, 2, 6, 3, 1, 5, 0, 7]](/wiki/images/math/a/3/e/a3e4109270a19cac82c7e91bec7564e4.png) , and our bound is
, and our bound is 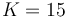 , then the longest intervals starting at each possible position that do not go over this bound are
, then the longest intervals starting at each possible position that do not go over this bound are ![[9, 2], [2, 6, 3, 1], [6, 3, 1, 5, 0], [3, 1, 5, 0], [1, 5, 0, 7], [5, 0, 7], [0, 7], [7]](/wiki/images/math/1/8/f/18f5eee020a6b0312a7073a5d9acc10a.png) . Observe that as we advance the left edge, the right edge also advances. This is because when we advance the left edge, we decrease the sum, so the right edge "wants" to advance to increase the sum and bring it closer to
. Observe that as we advance the left edge, the right edge also advances. This is because when we advance the left edge, we decrease the sum, so the right edge "wants" to advance to increase the sum and bring it closer to 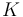 again. (Note that this doesn't work when there are negative numbers in the array.)
again. (Note that this doesn't work when there are negative numbers in the array.)
Here is the pseudocode. In the below, A is a zero-indexed array of length n. At each possible position for the left edge of the window, we advance the right edge as far as we can without going over the bound K. Then we advance the left edge. The variable sum keeps track of the sum so far.
input n, A, K
best ← 0
l ← 0
r ← 0
sum ← 0
while l < n
// The inner 'while' loop will not change the asymptotic complexity of O(N) , because r is incremented at most N times
// during the whole execution
while(r < n) and ( sum + A[r] ≤ K ) // then we can advance the right edge
sum ← sum + A[r]
r ← r + 1
best ← max(best, r-l)
sum ← sum - A[l] // now advance the left edge
l ← l + 1
A similar problem asks us to find the longest interval of an array in which no element is repeated. This is solved in essentially the same way. We start with an empty window, 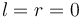 . Then we repeatedly advance the right edge until we hit an element we've already seen somewhere in the window; at this point, we have to start advancing the left edge until we remove the previous occurrence of that value. Then the right edge starts advancing again, and so on.
. Then we repeatedly advance the right edge until we hit an element we've already seen somewhere in the window; at this point, we have to start advancing the left edge until we remove the previous occurrence of that value. Then the right edge starts advancing again, and so on.
Problems
- CCC '96 - Maximum Distance
- CCC '03 - Longest Substring
- IOI '06 - Deciphering the Mayan Writing
- Broken Keyboard @ SPOJ
- Finding Seats @ SPOJ
- Matrix @ SPOJ
- Hotels Along the Croatian Coast @ SPOJ
- Cost @ SPOJ