Game theory
Game theory is the formal study of mathematical games. The ultimate goal of game theory is usually to solve a game; that is, to determine the nature of an optimal strategy for each player, and the outcome of such a strategy. Often, solving a game entails lengthy calculations, necessitating the use of a computer. However, brute force computational power is usually insufficient and clever mathematical reasoning is needed to invent efficient algorithms. Thus, game theory lies at a crossroads between mathematics and computer science.
Basic concepts
The terms game, player, objective, and move denote axiomatic concepts in game theory and we will not attempt to define them here.
State
The state, position, or configuration of a game, loosely put, consists of exactly that information which determines the valid moves that can be made in the future and is itself modified when moves take place. In a deterministic game (see below), the state, taken together with the players' strategies, is sufficient and necessary to determine the game's outcome. In a nondeterministic game, the same combination is sufficient and necessary to determine the probabilities of the possible outcomes of the game.
Determinism
A deterministic game is one in which the decisions of the players, reflected in the moves they make, are sufficient to determine the game's outcome. The opposite is an indeterministic game. More simply, "games of chance" are nondeterministic, whereas pure strategy games with no element of chance are deterministic. Chess, for example, is a deterministic game, whereas backgammon is not. Deterministic games are of greater mathematical interest than nondeterministic games, but both can be studied with the aid of a computer.
Availability of information
When all players know the entire state of a game at any given time, the game is said to be perfect information. Perfect information games include chess, Go, and tic-tac-toe. Most games of interest in mathematics and computer science are perfect information games. In particular, games which have winning strategies for one of the players tend to be perfect-information. Imperfect information games include most card games, as each player usually hides cards from opponents.
Partiality
An impartial game is one which satisfies two conditions:
- The valid moves from a given position depend only upon the position itself and not upon which player is to move next.
- The outcome of the game is symmetric with respect to the players.
Most games fail the first condition. Chess, for example, fails the first, since we must know if the player moving next is player 1 or player 2 to determine whether that player is to move a white piece or a black piece. Games failing the second condition are much rarer in serious mathematical study. Nim is a archetype for the impartial game; pieces are shared between the two players and each has the same goal.
Play convention
An important class of games consists of those between two players in which there are only two possible outcomes: victory and loss. If the winner is the last player who is able to make a legal move, the game is said to follow the normal play convention. Otherwise, it is said to follow the misère play convention. Dominoes is an example of a normal play game.
N-positions and P-positions
In a two-player, deterministic, impartial game which is guaranteed to end in a finite number of moves, an N-position is a configuration such that the next player to make a move can force victory, and a P-position is a configuration such that the previous player who moved can force victory. In a normal-play game, a configuration in which no further moves are possible is a P-position, since the player who is supposed to move next cannot do so and loses; in a misère-play game, it is an N-position, since the player who moved last made the last move and hence lost.
Consider a configuration  of such a game and the configurations
of such a game and the configurations 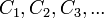 reachable from it. If at least one of
reachable from it. If at least one of 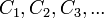 is a P-position, then the player presented with configuration
is a P-position, then the player presented with configuration  wants to make the move that results in that configuration, so that he or she becomes the previous player when the next player is to move --- guaranteeing victory. This makes
wants to make the move that results in that configuration, so that he or she becomes the previous player when the next player is to move --- guaranteeing victory. This makes  a N-position. If all of
a N-position. If all of 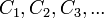 are N-positions, then no matter what move the current player makes, the next player can force victory, making
are N-positions, then no matter what move the current player makes, the next player can force victory, making  a P-position. In summary,
a P-position. In summary,
- If all positions reachable in one move from position
 are N-positions, then
are N-positions, then  is a P-position, and the current player does not have a winning strategy.
is a P-position, and the current player does not have a winning strategy. - Otherwise (at least one P-position is reachable from
 )
)  is an N-position, and a winning strategy necessarily entails leaving behind one of these P-positions for the next player.
is an N-position, and a winning strategy necessarily entails leaving behind one of these P-positions for the next player.
Nukit
The problem Nukit from the 2008 Canadian Computing Competition describes a game which is clearly two-player, deterministic, impartial, and guaranteed to end in a finite number of moves. Because of these properties we may analyze it with N-positions and P-positions. Given some position, we determine all valid reactions that can be formed (these are the moves) and consider the positions reachable by forming exactly one reaction. If these are all N-positions, the given position is a P-position, otherwise it is an N-position. As Patrick always moves first, Patrick wins whenever the configuration given in input is an N-position, and Roland wins when it is a P-position. This can be implemented with a recursive function that takes as parameters the number of particles of each type present; the base case occurs when no reaction can be formed. To solve the senior version, memoization or dynamic programming must be used to speed up this algorithm.
Nimbers
If, in addition to being deterministic, impartial, and guaranteed to end in a finite number of moves, a game is also normal play, it can be analyzed using the Sprague-Grundy theorem. We shall denote such games as Nim-like. (Note that this term is not in use in the academic literature.)
Nim
The name nimber alludes to what is perhaps the simplest interesting example of such a game: Nim. The rules of the game are as follows:
- The game board consists of one or more piles of sticks.
- On a player's turn, he or she chooses one non-empty pile and removes one or more sticks from it.
- The first player who cannot make a move loses. (That is, the player who takes the last stick wins.)
It is deterministic because the outcome of the game depends entirely upon the players' decisions and not upon any element of chance, it is perfect-information because we assume that both players know the sizes of all piles at any time, it is impartial because any move available to one player is available to the other and because both players have the same goal, it is normal play because the last to move wins, and it is guaranteed to end in a finite number of moves because each move removes at least one stick from the total count of sticks in play.
Winning strategy
We state here the solution to Nim, a well-known result, and show later how it fits into the framework of Nim-like games in general. Simply compute the bitwise XOR of the sizes of all piles gives the nim-sum of a configuration of Nim. If this is zero, then the configuration is a P-position; otherwise it is an N-position. For example, if there are three piles containing one, two, and three sticks, respectively, the nim-sum is 1 XOR 2 XOR 3 = 0, and the configuration is a P-position; however, if instead of a three-stick pile we had a four-stick pile, the nim-sum would be instead 1 XOR 2 XOR 4 = 7, and the configuration would be a N-position.
If, on your turn, you are faced with a P-position, it doesn't matter what you do; your opponent can force you to lose. If, on the other hand, you are faced with an N-position, you want to leave a P-position for your opponent. In the example with one, two, and four sticks, you would want to take one stick from the four-stick pile, leaving behind one, two, and three sticks for your opponent: a P-position. Repeatedly applying this strategy guarantees victory.
Nimbers in Nim
The nimber of a position in Nim is equal to its nim-sum, as defined above: the nimber of a single pile of sticks is simply the number of sticks in it, and the nimber of a collection of piles is the bitwise XOR of the nimbers of the individual piles.
Disjunctive sum of games
In some cases, a position in a game may be analyzed as the disjunctive sum of two or more sub-positions of the same game. This means that a player chooses exactly one of those sub-positions and makes exactly one valid move in it. Thus, if we divide the piles in a game of Nim up into two or more groups, each can be considered to constitute a separate game of Nim and a player must choose exactly one group and make a move in that group as though it were a separate game.
Statement of the theorem
The Sprague-Grundy theorem is the remarkable result that a nimber can be assigned to any configuration of any Nim-like game. This means that nimbers are useful in the analysis of not only Nim itself but of any Nim-like game. There are only a few simple rules for assigning nimbers:
- A nimber is a non-negative integer. (In general it may be any ordinal number, but we restrict ourselves to the finite case here.)
- The nimber of a position is the smallest possible value that does not appear among the nimbers of positions reachable from it in a single move, sometimes called the mex (minimal excluded ordinal). For example, if no moves are possible from a given configuration, the nimber is zero. If moves possible from a given configuration lead to other configurations with nimbers of 3, 0, 5, and 2, then the nimber for the given configuration is 1: the smallest non-negative integer that doesn't appear among these.
- The nimber of a disjunctive sum of games is equal to the bitwise XOR of the nimbers of the sub-games. This can be derived from the mex rule, and is included for convenience.
Application to Nim
Consider a single pile of sticks. If it contains zero sticks, no move is possible, and the nimber is 0 (rule 2). If it contains one stick, then a configuration with nimber zero (no sticks) is reachable from it, and thus the nimber must be 1. If it contains two sticks, it is possible to reach configurations with nimbers of zero and one, and thus the nimber must be 2... and so on. By induction, it is obvious that the nimber of a single pile of sticks in Nim is simply the number of sticks in the pile, as noted previously.
Now consider the general position, in which there are multiple piles of sticks. We may consider the whole position to be the disjunctive sum of individual piles. Thus, the nimber of the position is the bitwise XOR of the nimbers of the individual piles --- that is, the bitwise XOR of the sizes of the individual piles. Again, this is the same as the result noted above.
Interpreting nimbers
We stated that the nimber of a configuration from which no further move is possible is zero. As a matter of fact, in general, any P-position has a nimber of zero, and any position with a nimber of zero is a P-position. Similarly, an N-position always has a nonzero nimber, and a nonzero nimber always corresponds to an N-position. This completes our analysis of Nim: it now matches exactly the winning strategy stated previously.
Application to PEG-O-Stripes
Consider now the problem PEG-O-Stripes from the Woburn Challenge. The rules are simple:
- Constants
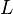 ,
, 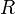 ,
,  , and
, and  are given.
are given. - The game is played on a one-dimensional board containing
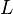 squares, initially empty.
squares, initially empty. - There is an unlimited supply of red strips, blue strips, and green strips. A red strip consists of
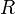 squares, a blue strip consists of
squares, a blue strip consists of  squares, and a green strip consists of
squares, and a green strip consists of  squares.
squares. - A move consists of placing one strip on the board. Strips may not overlap, and any square covered by a strip must be completely covered.
- The first player who cannot move loses.
The problem asks us to determine which of the two players has a winning strategy: that is, whether the initial position is an N-position or a P-position. It can be readily verified that PEG-O-Stripes is a Nim-like game. Let us now assign nimbers to configurations.
Note that once a strip is placed, the squares to its left and the squares to its right are permanently segregated; any further strips placed must occupy either squares to its left or squares to its right, but never both. Therefore, once a strip is placed, the game is split into a disjunctive sum of two games. Therefore, we only need to consider empty boards; any configuration of PEG-O-Stripes can be analyzed as a disjunctive sum of these.
Thus, we compute nimbers of boards of size  bottom-up by dynamic programming. Given an empty board, we consider all possible moves; that is, we try placing strips of every possible color at every possible position. (If
bottom-up by dynamic programming. Given an empty board, we consider all possible moves; that is, we try placing strips of every possible color at every possible position. (If 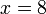 and
and 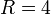 , for example, there are 5 ways to place a red strip on the board.) We find the nimbers of all configurations thus reachable, remembering that if the strip divides the board up into a smaller board on the left and a smaller board on the right, the nimber of the new configuration is the bitwise XOR of the nimbers of the smaller boards (Rule 3), and then we apply Rule 2 to find the nimber of the board of size
, for example, there are 5 ways to place a red strip on the board.) We find the nimbers of all configurations thus reachable, remembering that if the strip divides the board up into a smaller board on the left and a smaller board on the right, the nimber of the new configuration is the bitwise XOR of the nimbers of the smaller boards (Rule 3), and then we apply Rule 2 to find the nimber of the board of size  . Letting
. Letting  range from 0 to
range from 0 to 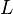 , at the termination of the algorithm a nimber is assigned to the given initial configuration, and the problem is solved.
, at the termination of the algorithm a nimber is assigned to the given initial configuration, and the problem is solved.