Constant optimization
Constant optimization refers to optimizing a program in order to improve its performance by at most a constant factor, that is, decreasing the invisible constant factor on the program's running time, memory usage, and so on. It usually involves changing details of the implementation rather than the underlying algorithm. One example of constant optimization is loop unrolling, which refers to replacing the body of a for loop with two or more iterations of itself so that the loop will only run half as many times, or fewer; this does not change the amount of work done inside the loop, but it means the termination condition will be checked less often, thus reducing the total number of instructions the CPU has to execute; this will decrease the running time by at most a constant factor.
Constant optimization is sometimes required in order to score full points on a contest problem with a "tight" time limit. If there are up to 100000 lines of input and you write a program whose algorithm is 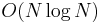 , your program might be too slow; on the other hand, if your algorithm is
, your program might be too slow; on the other hand, if your algorithm is 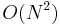 , then it is almost certainly too slow, and trying to optimize it to
, then it is almost certainly too slow, and trying to optimize it to 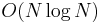 should be undertaken before optimizing the constant factor.
should be undertaken before optimizing the constant factor.