Computational geometry
Contents
- 1 Introduction and Scope
- 2 Points
- 3 Lines
- 3.1 What is a line?
- 3.2 The equation of a line
- 3.3 Standard Form of the equation of a line
- 3.4 Slope and intercepts of the line in standard form
- 3.5 Determining if a point is on a line
- 3.6 Construction of the line through two given points
- 3.7 Parallel and coincident lines
- 3.8 Finding the point of intersection of two lines
- 3.9 Direction numbers for a line
- 3.10 Parametric equation of a line
- 3.11 Translation along a line
- 3.12 Dropping a perpendicular
- 3.13 The distance from a point to a line
- 3.14 On which side of a line does a point lie?
- 3.15 The distance between two lines
- 3.16 Translating a line
- 4 Line segments
- 4.1 Introduction to line segments
- 4.2 Coincidence (equivalence) of line segments
- 4.3 Length of a line segment
- 4.4 Partitioning by length
- 4.5 Containing line
- 4.6 Determining if a point lies on a line segment
- 4.7 Intersection of line segments
- 4.8 Do two line segments cross?
- 4.9 Direction numbers for the containing line
- 4.10 Perpendicular bisector of a line segment
- 4.11 Conclusion - lines and line segments
- 5 Angles
- 6 Vectors
- 7 Circles
Introduction and Scope
Definition
Computational geometry, as one can easily guess from the name, is the branch of computer science encompassing geometrical problems and how their solutions may be implemented (efficiently, one would hope) on a computer.
Scope
Essentially all of the computational geometry you will encounter in high-school level competitions, even
competitions such as the IOI, is plane Euclidean geometry, the noble subject on which Euclid wrote his
Elements and a favorite of mathematical competitions. You would be hard-pressed to find contests containing geometry problems in three dimensions or higher. You also do not need to worry about non-Euclidean
geometries in which the angles of a triangle don't quite add to 180 degrees, and that sort of thing. In short,
the type of geometry that shows up in computer science contests is the type of geometry to which you have
been exposed, countless times, in mathematics class, perhaps without being told that other geometries exist.
So in all that follows, the universe is two-dimensional, parallel lines never meet, the area of a circle with
radius  is
is 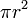 , and so on. This article discusses basic two-dimensional computational geometry; more advanced topics, such as computation of convex hulls, are discussed in separate articles.
, and so on. This article discusses basic two-dimensional computational geometry; more advanced topics, such as computation of convex hulls, are discussed in separate articles.
Points
Introduction to points
Many would claim that the point is the fundamental unit of geometry. Lines, circles, and polygons are all merely (infinite) collections of points and in fact we will initially consider them as such in order to derive several important results. A point is an exact location in space. Operations on points are very easy to perform computationally, simply because points themselves are such simple objects.
Representation: Cartesian coordinates
In our case, "space" is actually a plane, two-dimensional. That means that we need two real numbers to
describe any point in our space. Most of the time, we will be using the Cartesian (rectangular) coordinate
system. In fact, when points are given in the input of a programming problem, they are almost always
given in Cartesian coordinates. The Cartesian coordinate system is easy to understand and every pair of
real numbers corresponds to exactly one point in the plane (and vice versa), making it an ideal choice for
computational geometry.
Thus, a point will be represented in the computer's memory by an ordered pair of real numbers. Due to the
nature of geometry, it is usually inappropriate to use integers, as points generally do not fit neatly into the
integer lattice! Even if the input consists only of points with integer coordinates, calculations with these
coordinates will often yield points with non-integral coordinates, which can often cause counter-intuitive
behavior that will have you scratching your head! For example, in C++, when one integer is divided by
another, the result is always truncated to fit into an integer, and this is usually not desirable.
Determining whether two points coincide
Using the useful property of the Cartesian coordinate system discussed above, we can determine whether
or not two given points coincide. Denote the two points by  and
and  , with coordinates
, with coordinates 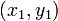 and
and 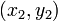 , respectively, and then:
, respectively, and then:
Read: The statement that  and
and  are the same point is equivalent to the statement that their corresponding coordinates are equal. That is,
are the same point is equivalent to the statement that their corresponding coordinates are equal. That is,  and
and  having both the same x-coordinates and also the same y-coordinates is both sufficient and necessary for the two to be the same point.
having both the same x-coordinates and also the same y-coordinates is both sufficient and necessary for the two to be the same point.
The distance between two points
To find the distance between two points, we use the Euclidean formula. Given two points 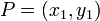 and
and 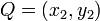 , the distance between them is given by:
, the distance between them is given by:
(Note that when we write 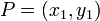 , we mean that
, we mean that  is a point with x-coordinate
is a point with x-coordinate 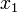 and y-coordinate
and y-coordinate 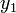 .)
.)
The midpoint of the line segment joining two points
Given two points, how may we find the midpoint of the line segment joining two points? (Intuitively, it is the point that is "right in the middle" of two given points. One might think that we require some knowledge about line segments in order to answer this, but it is for precisely the reason that, in a certain sense, no such knowledge is required to understand the answer, that this operation is found in the Points section. So, given two points 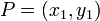 and
and 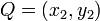 , this midpoint is given by
, this midpoint is given by
Lines
What is a line?
In axiomatic geometry, some terms such as point and line are left undefined, because an infinite regression of definitions is clearly absurd. In the algebraic approach we are taking, the line is defined in terms of the points which lie on it; that will be discussed in the following section. It will just be pointed out here that the word line is being used in the modern mathematical sense. Lines are straight; the terms line and straight line shall have identical meaning. Lines extend indefinitely in both directions, unlike rays and line segments.
The equation of a line
In computational geometry, we have to treat all aspects of geometry algebraically. Computers are excellent at dealing with numbers but have no mechanism for dealing with geometrical constructions; rather we must reduce them to algebra if we wish to accomplish anything.
In Ontario high schools, the equation of a line is taught in the ninth grade. For example, the line which passes through the points (0,1) and (1,0) has the equation 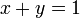 . Precisely, this means that for a given point
. Precisely, this means that for a given point 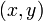 , the statement
, the statement 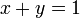 is equivalent to, or sufficient and necessary for, the point to be on the line.
is equivalent to, or sufficient and necessary for, the point to be on the line.
The form of the equation of the line which is first introduced is generally the 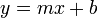 , in which
, in which 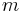 is the slope of the line and
is the slope of the line and 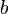 is the y-intercept. For example, the line discussed above has the equation
is the y-intercept. For example, the line discussed above has the equation 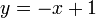 , that is,
, that is, 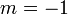 and
and 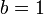 . By substituting different values for
. By substituting different values for 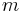 and
and 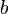 , we can obtain various (different) lines. But there's a problem here: if your line is vertical, then it is not
possible to choose values of
, we can obtain various (different) lines. But there's a problem here: if your line is vertical, then it is not
possible to choose values of 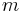 and
and 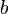 for the line. (Try it!) This is because the y-coordinate is no longer a function of the x-coordinate.
for the line. (Try it!) This is because the y-coordinate is no longer a function of the x-coordinate.
Thus, when dealing with lines computationally, it seems we would need to have a special case: check if the line is vertical; if so, then do something, otherwise do something else. This is a time-consuming and error-prone way of coding.
Standard Form of the equation of a line
Even though the slope-intercept form cannot describe a vertical line, there is an equation that describes a vertical line. For example, the line passing through (3,1) and (3,8) is 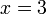 . In fact, almost any line can be described by an equation of the form
. In fact, almost any line can be described by an equation of the form 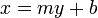 . (Try it if you don't believe me. I have merely switched around
. (Try it if you don't believe me. I have merely switched around  and
and 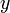 from the slope-intercept form.) Except... horizontal lines. So we have two forms of the equation of a line: one which fails on vertical lines and one which fails on horizontal lines. Can we combine them to give an equation of the line which is valid for any
line?
from the slope-intercept form.) Except... horizontal lines. So we have two forms of the equation of a line: one which fails on vertical lines and one which fails on horizontal lines. Can we combine them to give an equation of the line which is valid for any
line?
As it turns out, it is indeed possible.
That equation, the standard form of the equation of the line is:
By substituting appropriate values of  ,
,  , and
, and 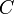 , one can
describe any line with this equation. And by storing values of
, one can
describe any line with this equation. And by storing values of  ,
,  , and
, and 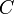 , one can represent a line in the computer's memory.
Here are some pairs of points and possible equations for each:
, one can represent a line in the computer's memory.
Here are some pairs of points and possible equations for each:
As you can see, it handles vertical and horizontal lines properly, as well as lines which are neither.
Note that the standard form is not unique: for example, the equation of the
first line could have just as well been 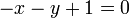 or perhaps
or perhaps
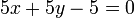 . Any given line has infinitely many representations
in the standard form. However, each standard form representation describes
at most one line.
. Any given line has infinitely many representations
in the standard form. However, each standard form representation describes
at most one line.
If  and
and  are both zero, the standard form describes no line
at all.
are both zero, the standard form describes no line
at all.
Slope and intercepts of the line in standard form
By isolating 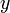 from the standard form, we obtain the slope and y-intercept
form for line
from the standard form, we obtain the slope and y-intercept
form for line  (
(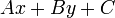 ) when
) when 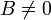 (that is, when
the line is not vertical):
(that is, when
the line is not vertical):
The y-intercept is obtained by letting 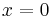 and then:
and then:
Similarly, the x-intercept is given by:
In order for the x-intercept to exist, the line must not be horizontal, that
is, 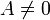 .
.
Determining if a point is on a line
Using the definition of the equation of a line, it becomes evident that
to determine whether or not a point lies on a line, we simply substitute its
coordinates into the equation of the line, and check if the LHS is, indeed,
equal to zero. This allows us to determine, for example, that 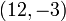 is on the last line given in the table above, whereas
is on the last line given in the table above, whereas 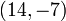 is not
on that line.
is not
on that line.
Construction of the line through two given points
A good question is: how do we determine that fourth equation above, the equation of the line through (6,6) and (4,9)? It's not immediately obvious from the two points given, whereas the other three are pretty easy.
For the slope-y-intercept form 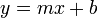 , you first determined the slope
, you first determined the slope
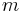 , and then solved for
, and then solved for 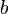 . A similar procedure can be used for
standard form.
We state here the following pseudocode for determining the
coefficients
. A similar procedure can be used for
standard form.
We state here the following pseudocode for determining the
coefficients  ,
,  ,
, 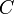 of the equation of the line through
points
of the equation of the line through
points 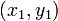 and
and 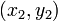 in standard form:
in standard form:
(It is one thing to derive a formula or algorithm and quite another thing to prove it. The derivation of this formula is not shown, but proving it is as easy as substituting to determine that the line really does pass through the two given points.)
Parallel and coincident lines
In the slope and y-intercept form, two lines are either parallel or coincident if they
have the same slope. So given two lines 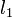 (
(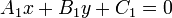 ) and
) and 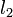 (
(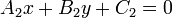 ),
we obtain, for
),
we obtain, for 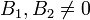 :
:
Cross-multiplying gives a result that is valid even if either or both lines are vertical, that is, it is valid for any pair of lines in standard form:
Now, in the slope-y-intercept form, two lines coincide if their slopes and y-intercepts both coincide. In a manner similar to that of the previous section, we obtain:
or, if x-intercepts are used instead:
Two lines coincide if 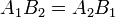 and either of the two
equations above holds. (As a matter of fact, if the two lines are coincident,
they will both hold, but only one of them needs to be checked.) If
and either of the two
equations above holds. (As a matter of fact, if the two lines are coincident,
they will both hold, but only one of them needs to be checked.) If
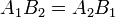 but the lines are not coincident, they are parallel.
but the lines are not coincident, they are parallel.
Finding the point of intersection of two lines
If two lines are coincident, every point on either line is an intersection point. If they are parallel, then no intersection points exist. We consider the general case in which neither is true.
In general, two lines intersect at a single point. That is, the intersection
point is the single point that lies on both lines. Since it lies on both lines,
it must satisfy the equations of both lines simultaneously. So to find the
intersection point of 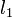
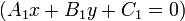 and
and 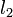
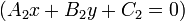 , we seek the ordered pair
, we seek the ordered pair 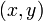 which satisfies:
which satisfies:
This is a system of two linear equations in two unknowns and is solved by
Gaussian elimination. Multiply the first by 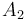 and the second by
and the second by 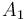 , giving:
, giving:
Subtracting the former from the latter gives, with cancellation of the  term:
term:
Instead of redoing this to obtain the value of  , we take advantage of
symmetry and simply swap all the
, we take advantage of
symmetry and simply swap all the  's with the
's with the  's. (If you don't
believe that this works, do the derivation the long way.)
's. (If you don't
believe that this works, do the derivation the long way.)
or:
Notice the quantity 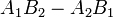 , and how it forms the denominator
of the expressions for both
, and how it forms the denominator
of the expressions for both  and
and 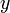 . When solving for the
intersection point on the computer, you only need to calculate this quantity
once. (This quantity, called a determinant, will resurface later on.)
Here is pseudocode for finding the intersection point:
. When solving for the
intersection point on the computer, you only need to calculate this quantity
once. (This quantity, called a determinant, will resurface later on.)
Here is pseudocode for finding the intersection point:
When 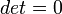 , the lines are either parallel or coincident. We now see
algebraically that the division by zero prevents us from finding a unique
intersection point for such pairs of lines.
, the lines are either parallel or coincident. We now see
algebraically that the division by zero prevents us from finding a unique
intersection point for such pairs of lines.
Direction numbers for a line
This in itself is not very useful, but it will become important in the following sections as a simplifying concept.
Lines are straight; effectively they always point in the same direction. One
way to express that direction has been slope, which unfortunately is undefined
for vertical lines. The slope 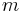 for a line told us that you could
start at any point on the line, move
for a line told us that you could
start at any point on the line, move 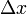 units to the right, then
move
units to the right, then
move 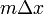 units up, and you would again be located on the line.
Thus we can say that
units up, and you would again be located on the line.
Thus we can say that 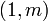 is a pair of direction numbers for that line.
This means that if
is a pair of direction numbers for that line.
This means that if 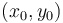 is on a line, and
is on a line, and 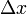 and
and
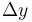 are in the ratio
are in the ratio 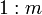 , for that line, then
, for that line, then
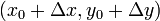 is on the same line. This means that
is on the same line. This means that
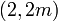 is also a set of direction numbers for that line, or, indeed, any
multiple of
is also a set of direction numbers for that line, or, indeed, any
multiple of 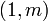 other than
other than 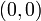 . (
. (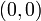 clearly tells you nothing about the line.)
clearly tells you nothing about the line.)
We can define something similar for the line in standard form. Choose some
starting point 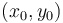 on line
on line  . Now, move to a new point
. Now, move to a new point
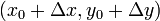 . In order for this point to be on the line
. In order for this point to be on the line
 , we must have
, we must have
Expanding and rearranging gives
We know that 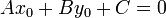 since
since 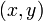 is on line
is on line  .
Therefore,
.
Therefore,
Convince yourself, by examining the equation above, that 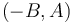 is a set
of direction numbers for line
is a set
of direction numbers for line  . Similarly, if we have a pair of
direction numbers
. Similarly, if we have a pair of
direction numbers 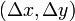 , although this does not define a
unique line, we can obtain possible values of
, although this does not define a
unique line, we can obtain possible values of  and
and  as
as
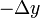 and
and 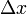 , respectively.
, respectively.
The relationship between direction numbers and points on the corresponding line
is an "if-and-only-if" relationship. If 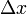 and
and 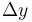 are
in the ratio
are
in the ratio 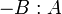 , then we can "shift" by
, then we can "shift" by 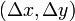 ,
and vice versa.
,
and vice versa.
Any line perpendicular to  will have the direction numbers
will have the direction numbers 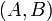 ,
and thus a possible equation starts
,
and thus a possible equation starts 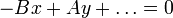 .
(This is the same as saying, for non-vertical lines, that the product of slopes
of perpendicular lines is -1. Examine the equation for the slope of a line
given in standard form and you'll see why.) In fact, in an algebraic treatment of geometry
such as this, we do not prove this claim, but instead proclaim it the definition of
perpendicularity: given two lines with direction numbers
.
(This is the same as saying, for non-vertical lines, that the product of slopes
of perpendicular lines is -1. Examine the equation for the slope of a line
given in standard form and you'll see why.) In fact, in an algebraic treatment of geometry
such as this, we do not prove this claim, but instead proclaim it the definition of
perpendicularity: given two lines with direction numbers 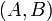 and
and
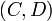 , they are perpendicular if and only if
, they are perpendicular if and only if
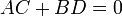 .
.
Given some line, all lines parallel to that one have the same direction numbers. That is, the direction numbers, while providing information about a line's direction, provide no information about its position. However, sometimes all that is needed is the direction, and here the direction numbers are very useful.
Parametric equation of a line
Given some line 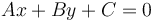 and a point
and a point 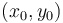 known to be on the line, we can use the direction numbers to write the parametric equation of the line. Since
known to be on the line, we can use the direction numbers to write the parametric equation of the line. Since 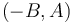 is a set of direction numbers for the line, we see that
is a set of direction numbers for the line, we see that 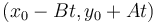 will be on the line for any
will be on the line for any 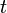 , and furthermore each point on the line corresponds to exactly one value of
, and furthermore each point on the line corresponds to exactly one value of 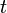 in this way.
in this way.
Translation along a line
Given some line 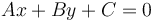 and a point
and a point 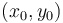 known to be on the line, we wish to locate another point on the line that is distance
known to be on the line, we wish to locate another point on the line that is distance 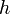 away from
away from 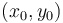 . We can do this by observing that the general point is given by
. We can do this by observing that the general point is given by 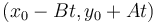 , which is distance
, which is distance 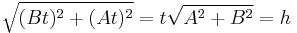 away from
away from 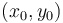 . Therefore, we want
. Therefore, we want 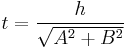 , and finally obtain
, and finally obtain 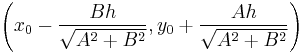 . Note that unless
. Note that unless 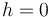 , there is another possible answer, which is simply "on the other side":
, there is another possible answer, which is simply "on the other side": 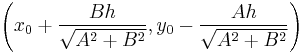 .
.
Dropping a perpendicular
Given a line 
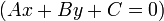 and a point
and a point 
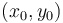 which may or may not be on
which may or may not be on  , can we find the line perpendicular to
, can we find the line perpendicular to
 passing through
passing through  ? By Euclid's Fifth Postulate, there exists
exactly one such line. The algorithm to find it is given below:
? By Euclid's Fifth Postulate, there exists
exactly one such line. The algorithm to find it is given below:
where 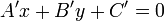 is the perpendicular line desired.
is the perpendicular line desired.
There is nothing difficult to memorize here: we already noted in the previous
section how to find the values of 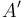 and
and 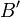 , and finding the value
of
, and finding the value
of 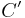 is merely setting
is merely setting 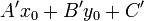 equal to zero (so that the
point
equal to zero (so that the
point 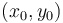 will be on the resulting line).
will be on the resulting line).
The foot of the perpendicular is the point at which it intersects the
line  . It is guaranteed to exist since two lines cannot, of course, be
both perpendicular and parallel. Combining the above algorithm with the line intersection algorithm
explained earlier gives a solution for the location of the point. A bit of algebra gives
this optimized algorithm:
. It is guaranteed to exist since two lines cannot, of course, be
both perpendicular and parallel. Combining the above algorithm with the line intersection algorithm
explained earlier gives a solution for the location of the point. A bit of algebra gives
this optimized algorithm:
where 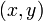 are the coordinates of the foot of the perpendicular from
are the coordinates of the foot of the perpendicular from
 to
to  .
.
The distance from a point to a line
By the distance from a point 
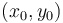 to a line
to a line 
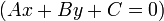 what is meant is the closest possible distance from
what is meant is the closest possible distance from  to any point on
to any point on  . What point on
. What point on  is closest to
is closest to  ?
It is intuitive perhaps that it is obtained by dropping a perpendicular
from
?
It is intuitive perhaps that it is obtained by dropping a perpendicular
from  to
to  . That is, we choose a point
. That is, we choose a point  such that
such that
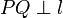 , and the distance from
, and the distance from  to
to  is then the length
of line segment
is then the length
of line segment 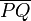 , denoted
, denoted 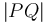 .
.
The reason why this is the shortest distance possible is this: Choose any other
point 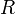 on
on  . Now,
. Now, 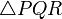 is right-angled at
is right-angled at  .
The longest side of a right triangle is the hypotenuse, so that
.
The longest side of a right triangle is the hypotenuse, so that
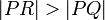 . Thus
. Thus 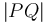 is truly the shortest possible distance.
is truly the shortest possible distance.
Now, as noted earlier, the line 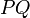 , being perpendicular to
, being perpendicular to  , has the direction numbers
, has the direction numbers 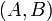 . Thus, for any
. Thus, for any 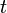 , the point
, the point 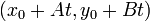 is on
is on
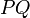 . For some choice of
. For some choice of 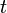 , this point must coincide with
, this point must coincide with  .
Since that point lies on
.
Since that point lies on  , we have
, we have
This instantly gives the formula for the foot of the perpendicular given in the previous section.
Now, the distance 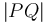 is found with the Euclidean formula:
is found with the Euclidean formula:
The last line is the formula to remember. To restate,
(It was noted earlier that if  and
and  are both zero, then
we don't actually have a line. Therefore, the denominator above can never be
zero, which is a good thing.)
are both zero, then
we don't actually have a line. Therefore, the denominator above can never be
zero, which is a good thing.)
On which side of a line does a point lie?
A line partitions the plane into two regions. For example, a vertical line
divides the plane into a region on the left and a region on the right. Now,
when a point 
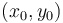 does not satisfy the equation of a line
does not satisfy the equation of a line

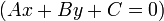 , can we determine on which side of the line it lies?
, can we determine on which side of the line it lies?
Yes we can, with a certain restriction. If 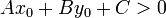 , then the
point lies on one side of the line; if
, then the
point lies on one side of the line; if 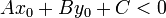 , then it lies
on the other side. However, it's a bit pointless to say which side it
lies on: does it lie on the left or the right? If the line is horizontal, then
this question becomes meaningless. Also, notice that if we flip the signs of
, then it lies
on the other side. However, it's a bit pointless to say which side it
lies on: does it lie on the left or the right? If the line is horizontal, then
this question becomes meaningless. Also, notice that if we flip the signs of
 ,
,  , and
, and 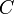 , then the value of
, then the value of 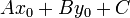 is
negated also, but that changes neither the point or the line. It is enough,
however, to tell if two points are on the same side of the line or on opposite
sides; simply determine whether
is
negated also, but that changes neither the point or the line. It is enough,
however, to tell if two points are on the same side of the line or on opposite
sides; simply determine whether 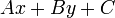 has the same sign for both,
or different signs.
has the same sign for both,
or different signs.
The distance between two lines
If two lines intersect, the closest distance between them is zero, namely at
their intersection point. If they are coincident, then the distance is
similarly zero. If two lines are parallel, however, there is a nonzero distance
between them, and it is defined similarly to the distance between a point and a
line. To find this distance, we notice that the lines
 and
and 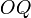 are coincident, where
are coincident, where 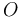 is the origin,
is the origin,  is
the foot of the perpendicular from
is
the foot of the perpendicular from 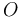 to
to 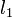 , and
, and  is the
foot of the perpendicular from
is the
foot of the perpendicular from 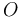 to
to 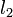 . We know, by substituting
. We know, by substituting
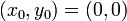 for both
for both 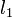 (
(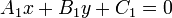 ) and
) and
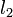 (
(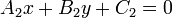 ) that:
) that:
Now here we come up against a complication. If 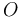 is on the line
segment
is on the line
segment 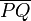 , then we have to add
, then we have to add 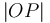 and
and
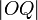 to get the desired
to get the desired 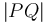 . That is, if
. That is, if 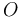 is on the same
side of both lines. Otherwise, we have to take the difference. Here's some
code that takes care of these details:
is on the same
side of both lines. Otherwise, we have to take the difference. Here's some
code that takes care of these details:
Translating a line
Suppose we are given a line 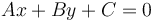 and we wish to find a line parallel to it such that the distance between these two lines is
and we wish to find a line parallel to it such that the distance between these two lines is 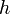 . To do this, we suppose that the new line has equation
. To do this, we suppose that the new line has equation 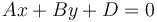 . Since the two lines have the same
. Since the two lines have the same  and
and  value, they must be parallel (or coincident of
value, they must be parallel (or coincident of 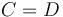 also). Then, the distance between them will be given by
also). Then, the distance between them will be given by 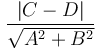 , as the previous section suggests. To obtain a value of
, as the previous section suggests. To obtain a value of  for this expression, it is not hard to see that we should choose
for this expression, it is not hard to see that we should choose 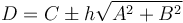 .
.
Line segments
Introduction to line segments
A line segment is the part of a line located "between" two points on that
line, called endpoints. Any pair of points defines a unique line
segment. Most definitions of "line segment" allow the endpoints to coincide,
giving a single point, but this case will often not arise in programming
problems and it is trivial to handle when it does arise, so we will not discuss
it here; we assume the endpoints must be distinct. Thus, every line segment
defines exactly one line.
We may represent a line segment in memory as a pair of points: that is, four
numbers in total.
Coincidence (equivalence) of line segments
Two line segments coincide if they have the same endpoints. However, they may have them in any order, hence we have:
(The parentheses are unnecessary and are added only for the sake of clarity.)
Length of a line segment
The length of a line segment is nothing more than the distance between its endpoints.
Partitioning by length
Suppose we wish to partition a line segment 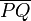 by introducing
a point
by introducing
a point 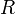 on
on 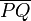 such that
such that 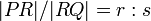 . That
is, we wish to partition it into two line segments with their lengths in the
ratio
. That
is, we wish to partition it into two line segments with their lengths in the
ratio 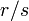 . We may do so as follows:
. We may do so as follows:
In the special case that  , we have the midpoint, as discussed in the Points section.
, we have the midpoint, as discussed in the Points section.
Containing line
All we have to do is find the line passing through both endpoints; the algorithm to do this is discussed in the section "Construction of the line through two given points".
Determining if a point lies on a line segment
Here is one interesting idea: if a point 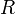 lies on segment
lies on segment 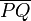 , then the relation
, then the relation
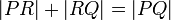 will hold. If it is on the line
will hold. If it is on the line 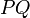 but
not on the segment
but
not on the segment 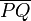 , then it is the difference
between
, then it is the difference
between 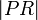 and
and 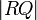 that will equal
that will equal 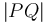 , not the sum. If
it is not on this line, then the points
, not the sum. If
it is not on this line, then the points  ,
,  , and
, and 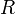 form a
triangle, and by the Triangle Inequality,
form a
triangle, and by the Triangle Inequality, 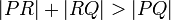 . Thus:
. Thus:
Although this test is mathematically ingenious, it should not be used in
practice, since the extraction of a square root is a slow operation. (Think about how much work it takes by hand, for example, to compute a square root, relative to carrying out multiplication or division by hand.)
A faster method is to obtain the line containing the line segment (see
previous section); if multiple queries are to be made on the same line segment
then it is advisable to store the values of  ,
,  , and
, and 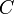 rather than computing them over and over again; and we first check if the point
to test is on the line; if it is, then we must check if it is on the
segment by checking if each coordinate of the point is between the
corresponding coordinates of the endpoints of the segment.
rather than computing them over and over again; and we first check if the point
to test is on the line; if it is, then we must check if it is on the
segment by checking if each coordinate of the point is between the
corresponding coordinates of the endpoints of the segment.
For a one-time query (when we do not expect to see the line again), the use of
the properties of similar triangles yields the following test: the point is on
the line segment if and only if 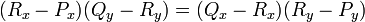 and
and  is between
is between  and
and  . When this test is used several
times with different segments, the number of multiplications required is only
half of the number required for the test via the containing line, but
if the line is reused, then the test via the containing line ends up
using fewer additions/subtractions in the long run.
. When this test is used several
times with different segments, the number of multiplications required is only
half of the number required for the test via the containing line, but
if the line is reused, then the test via the containing line ends up
using fewer additions/subtractions in the long run.
Intersection of line segments
Given two line segments  and
and  , how do we
determine whether they intersect?
, how do we
determine whether they intersect?
First, if the containing lines are coincident, then the line segments intersect
if and only if at least one of the endpoints of one of the segments is on the
other segment. In general, when the containing lines do not coincide,
the segments intersect if and only if  and
and
 are not on the same side of
are not on the same side of 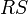 and
and 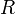 and
and  are
not on the same side of
are
not on the same side of 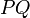 . That is, extend each segment to a line and
then determine on which sides of the line lie the endpoints of the other segment. (If one point is on the line and the other is not, then they are not considered to be on the same side, since two
line segments can intersect even if the endpoint of one lies on the other.)
. That is, extend each segment to a line and
then determine on which sides of the line lie the endpoints of the other segment. (If one point is on the line and the other is not, then they are not considered to be on the same side, since two
line segments can intersect even if the endpoint of one lies on the other.)
If the segments intersect, their intersection point can be determined by finding the intersection
point of the containing lines.
Another method for determining whether two line segments intersect is finding
the intersection point (if it exists) of the containing lines and checking if
it lies on both line segments (as in the end of the previous section). After
finding the containing lines, this method requires six multiplications and two
divisions, whereas the one above requires eight multiplications. Since
multiplications are generally faster, we prefer the method above to this one.
Do two line segments cross?
The word cross is used here in a stronger sense than intersect.
Two line segments cross if they intersect and no point of intersection is
an endpoint of either line segment. Intuitively, the two line segments form
a (possibly distorted) X shape. Here, we can ignore the degenerate cases for line segment
intersection: we simply test that  and
and  are on different sides of
are on different sides of
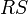 (this time the test fails if either of them is actually
on it), and that
(this time the test fails if either of them is actually
on it), and that 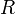 and
and  are on different sides of
are on different sides of 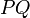 .
The second method described in the previous section can again be applied, although again
it is expected to be slower.
.
The second method described in the previous section can again be applied, although again
it is expected to be slower.
Direction numbers for the containing line
By the definition of the direction numbers, a set of direction numbers for the
line segment 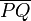 is
is 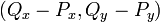 . This gives
an instant proof for the "magic formula" for the line through two given points: we convert
these direction numbers to values for
. This gives
an instant proof for the "magic formula" for the line through two given points: we convert
these direction numbers to values for  and
and  and then solve for
and then solve for
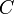 using one of the points.
using one of the points.
Perpendicular bisector of a line segment
The perpendicular bisector of a line segment is the line perpendicular to the
line segment which also passes through the line segment's midpoint. Notice that
the direction numbers obtained in the previous section can be used to obtain the
direction numbers for a perpendicular line, and that these can in turn be used
to reconstruct the values of  and
and  for that line. Given that the
line must also pass through the midpoint:
for that line. Given that the
line must also pass through the midpoint:
This technique requires a total of two multiplications and two divisions. If we
substitute the values of  and
and 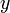 into the last line and expand, we
can change this to four multiplications and one division, which is almost
certainly slower as division by two is a very fast operation.
into the last line and expand, we
can change this to four multiplications and one division, which is almost
certainly slower as division by two is a very fast operation.
Conclusion - lines and line segments
The techniques of the two preceding chapters should provide inspiration on how to achieve tasks that are "somewhere in-between". For example, we have not discussed the intersection of a line and a line segment. However, it is fairly clear that all that is required is to test on which sides of the line lie the endpoints of the segment: half of the test for two line segments. We also have not discussed the distance from a point to a line segment. We have omitted any discussion of rays altogether. If you thoroughly understand how these techniques work, though, extending them to problems not explicitly mentioned should not be difficult. Feel free to add these sections to this article; the exclusion of any material from the current draft is not an indication that such material does not belong in this article.
Angles
Introduction to angles
In trigonometry, one proves the Law of Cosines. In a purely algebraic approach to geometry, however the concept of angle is defined using the Law of Cosines, and the Law itself requires no proof. Still, we will not use that definition directly, because deriving everything from it would be unnecessarily complicated. Instead, we will assume that we already know some properties of angles. Storing angles in memory is very easy: just store the angle's radian measure. Why not degree measure? Degree measure is convenient for mental calculation, but radian measure is more mathematically convenient and, as such, trigonometric functions of most standard language libraries, such as those of Pascal and C/C++, expect their arguments in radians. (Inverse trigonometric functions return results in radians.) We will use radian measure throughout this chapter, without stating "radians", because radian measure is assumed when no units are given.
Straightforward applications of basic trigonometry, such as finding the angles in a triangle whose vertices are known (Law of Cosines), are not discussed here.
Directed angle and the atan2 function
Suppose a ray with its endpoint at the origin initially points along the
positive x-axis and is rotated counterclockwise around the origin by an angle
of 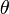 . From elementary trigonometry, the ray now consists of points
. From elementary trigonometry, the ray now consists of points
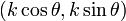 , where
, where 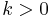 . This angle
. This angle 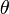 is a directed angle. Notice there is another ray with its endpoint at
the origin that makes an angle of
is a directed angle. Notice there is another ray with its endpoint at
the origin that makes an angle of 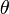 with the positive x-axis:
obtained by rotating clockwise rather than counterclockwise. But the directed
angle in this case would be
with the positive x-axis:
obtained by rotating clockwise rather than counterclockwise. But the directed
angle in this case would be 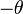 . Thus, by specifying a directed angle
from the positive x-axis
we can uniquely specify one particular ray.
. Thus, by specifying a directed angle
from the positive x-axis
we can uniquely specify one particular ray.
Can we reverse this process? Can we find the directed angle from the positive
x-axis to the ray 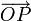 , where
, where 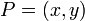 ? Notice that
when
? Notice that
when 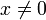 ,
, 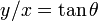 , so taking the inverse tangent
should give back
, so taking the inverse tangent
should give back 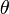 . There are just two problems with this: one is
that
. There are just two problems with this: one is
that  might be zero (but the angle will still be defined, either
might be zero (but the angle will still be defined, either 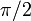 or
or 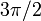 ), the other is that the point
), the other is that the point 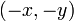 will give
the same tangent even though it lies on the other side (and hence its directed
angle should differ from that of
will give
the same tangent even though it lies on the other side (and hence its directed
angle should differ from that of 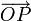 by
by 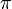 .
However, because this is such a useful application, the Intel FPU has a
built-in instruction to compute the directed angle from the positive x-axis to
ray
.
However, because this is such a useful application, the Intel FPU has a
built-in instruction to compute the directed angle from the positive x-axis to
ray 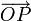 , and the libraries of both C and Free Pascal
contain functions for this purpose. C's is called
, and the libraries of both C and Free Pascal
contain functions for this purpose. C's is called atan2, and it takes
two arguments, 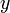 and
and  , in that order, returning an angle in
radians, the desired directed angle, a real number
, in that order, returning an angle in
radians, the desired directed angle, a real number 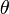 satisfying
satisfying
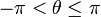 . (Notice that as with undirected angles, adding
. (Notice that as with undirected angles, adding
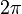 to a directed angle leaves it unchanged). Remember that
to a directed angle leaves it unchanged). Remember that 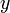 comes first and not
comes first and not  ; the reason for this has to do with the design of
the Intel FPU and the calling convention of C. Free Pascal's math library aims
to largely emulate that of C, so it provides the
; the reason for this has to do with the design of
the Intel FPU and the calling convention of C. Free Pascal's math library aims
to largely emulate that of C, so it provides the arctan2 function
which takes the same arguments and produces the same return value.
The angle between a line and the x-axis
When two lines intersect, two pairs of angles are formed (the two angles in
each pair are equal). They are supplementary. To find one of these angles, let
us shift the line until it passes through the x-axis. Then, adding the
direction numbers 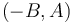 to the origin gives another point. We now apply
the
to the origin gives another point. We now apply
the atan2 function: atan2(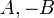 ). (Notice that we have
reversed the order of
). (Notice that we have
reversed the order of  and
and 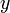 , as required.) The result may be
negative; we can add
, as required.) The result may be
negative; we can add 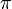 to it to make it non-negative.
to it to make it non-negative.
The angle between two lines
To find one of the two angles between two lines, we find the angle between each
line and the x-axis, then subtract. (Draw a diagram to convince yourself that
this works.) If the result is negative, add 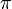 degrees, once or
twice as necessary. The other angle is obtained by subtracting from
degrees, once or
twice as necessary. The other angle is obtained by subtracting from 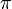 .
.
The angle bisector of a pair of intersecting lines
Using the result of the previous section and a great deal of algebra and trigonometry,
together with the line intersection algorithm, gives the following algorithm for finding one of the
two angle bisectors of a pair of (intersecting) lines 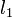
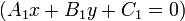 and
and 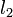
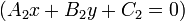 (the bisector
is represented as
(the bisector
is represented as 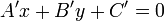 ):
):
The other angle bisector, of course, is perpendicular to this line and also passes through that intersection point.
Vectors
Introduction to vectors
Although the word vector has a formal definition, we will not find it useful. It is better, in the context of computational geometry, to think of a vector as an idealized object which represents a given translation. Visually, a vector may be represented as an arrow with a fixed length pointing in a fixed direction, but without a fixed location. For example, on the Cartesian plane, consider the translation "3 units down and 4 units right". If you start at the point (8,10) and apply this translation, (12,7) is obtained. This can also be represented as an arrow with length 5 units and direction approximately 37 degrees south of east. Placing the tail of this arrow at (8,10) results in the head resting upon the point (12,7). The vector from (0,0) to (4,-3) is the same vector, as it also represents a translation 3 units down and 4 units right, and has the same length and direction. However, the vector from (12,7) to (8,10) and the vector from (0,0) to (-3,4) are different from the one from (8,10) to (12,7); they have the same lengths, but their directions are different, and so they are different vectors. The vector from (0,0) to (8,-6) is also different; it has the same direction, but a different length. In both cases, these are simply different translations, and hence different vectors. The word vector is from the Latin, meaning carrier, appropriate as it carries from one location (a point) to another.
Representation
We could represent a vector by its magnitude and direction, but it is usually not convenient to do so. Even still, it might be useful occasionally to find the magnitude and direction of a vector; refer to the sections on length of a line segment and directed angle and the atan2 function for the necessary mathematics. Instead, we will use the Cartesian representation. If we place the tail of a vector on the origin, the head rests upon a certain point; the Cartesian coordinates of this point are the Cartesian components of the vector. We thus represent a vector as we do a point, as an ordered pair of real numbers, but we shall enclose these in brackets instead of parentheses. The vector discussed above is then [4,-3], as when the tail is placed on (0,0), the head rests upon (4,-3). Two vectors are equal when both of their corresponding components are equal.
Standard vector notation
In writing, vectors are represented as letters with small rightward-pointing arrows over them, e.g., 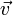 . Vectors are usually typeset in bold, e.g.,
. Vectors are usually typeset in bold, e.g., 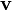 . We shall denote the components of
. We shall denote the components of 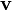 as
as 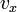 and
and 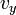 . The magnitude of
. The magnitude of 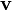 may be denoted simply
may be denoted simply  , or, to avoid confusion with an unrelated scalar variable,
, or, to avoid confusion with an unrelated scalar variable, 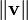 . There is a special vector known as the zero vector, the identity translation; it leaves one's position unchanged and has the Cartesian representation [0,0]. We shall represent it as
. There is a special vector known as the zero vector, the identity translation; it leaves one's position unchanged and has the Cartesian representation [0,0]. We shall represent it as 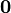 .
.
Basic operations
The order of operations is the same with vectors as with real numbers.
Addition
Addition of vectors shares many properties with addition of real numbers. It is represented by the plus sign, and is associative and commutative.
Of a vector to a point
Adding a vector to a point is another name for the operation in which a point is simply translated by a given vector. It is not hard to see that ![(x,y) + [u,v] = (x+u,y+v)](/wiki/images/math/0/9/c/09c5b912b9c75a1d54c9920bc4fb0e4f.png) . We could also write the same sum as
. We could also write the same sum as ![[u,v] + (x,y)](/wiki/images/math/2/6/a/26adad41d53fdcc1eabb9f9e521577fc.png) , since addition is supposed to be commutative. As one can easily see, adding a point and a vector results in another point. The zero vector is the additive identity; adding it to any point leaves the point unchanged. Geometrically, adding a point and a vector entails placing the vector's tail at the point; the vector's head then rests upon the sum.
, since addition is supposed to be commutative. As one can easily see, adding a point and a vector results in another point. The zero vector is the additive identity; adding it to any point leaves the point unchanged. Geometrically, adding a point and a vector entails placing the vector's tail at the point; the vector's head then rests upon the sum.
Of two vectors
If we want addition to be associative too, then the sum 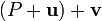 must be the same point as
must be the same point as 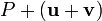 . The first sum represents the point arrived at when the translations representing
. The first sum represents the point arrived at when the translations representing 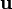 and
and 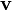 are taken in succession. Therefore, in the second sum, we should define
are taken in succession. Therefore, in the second sum, we should define 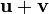 in such a way so that it gives a vector representing the translation obtained by taking those of
in such a way so that it gives a vector representing the translation obtained by taking those of 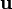 and
and 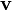 in succession. It is not too hard to see that
in succession. It is not too hard to see that ![[u_x,u_y] + [v_x,v_y] = [u_x+v_x,u_y+v_y]](/wiki/images/math/e/3/c/e3c1b9e43011fc034d363122cc4e1299.png) . Geometrically, if the tail of
. Geometrically, if the tail of 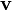 is placed at the head of
is placed at the head of 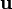 , the arrow drawn from the tail of
, the arrow drawn from the tail of 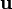 to the head of
to the head of 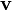 is the sum. Again, the zero vector is the additive identity.
is the sum. Again, the zero vector is the additive identity.
Negation
For every vector 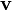 we can identify a corresponding vector, denoted
we can identify a corresponding vector, denoted 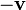 , such that the translations represented by
, such that the translations represented by 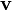 and
and 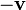 are inverse transformations. Another way of stating this is that
are inverse transformations. Another way of stating this is that 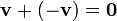 , or that
, or that 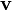 and
and 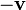 have the same length but opposite directions. If
have the same length but opposite directions. If ![\mathbf{v} = [v_x,v_y]](/wiki/images/math/7/7/6/776f4f508590bd4a4cba8642393e97e6.png) , then
, then ![-\mathbf{v} = [-v_x,-v_y]](/wiki/images/math/6/1/f/61f47b1ff85c975d1f727bf8f992371d.png) .
.
Subtraction
Of a vector from a point
We define subtraction to be the inverse operation of addition. That is, for any point  and vector
and vector 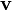 , we should have that
, we should have that 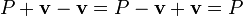 . Since the vector
. Since the vector 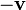 represents the inverse translation to
represents the inverse translation to 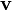 , we can simply add
, we can simply add 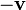 to
to  to obtain
to obtain 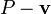 . (Note that the expression
. (Note that the expression 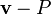 is not meaningful.) Geometrically, this is equivalent to placing the head of the arrow at
is not meaningful.) Geometrically, this is equivalent to placing the head of the arrow at  and then following the arrow backward to the tail. Subtracting the zero vector leaves a point unchanged.
and then following the arrow backward to the tail. Subtracting the zero vector leaves a point unchanged.
Of a vector from a vector
To subtract one vector from another, we add its negative. Again, we find that this definition leads to subtraction being the inverse operation of addition. It is not too hard to see that ![[u_x,u_y] - [v_x,v_y] = [u_x-v_x,u_y-v_y]](/wiki/images/math/8/b/9/8b90608ea207bc9267ddcbbaec2f6911.png) . Geometrically, if the vectors
. Geometrically, if the vectors 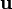 and
and 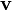 are placed tail-to-tail, then the vector from the head of
are placed tail-to-tail, then the vector from the head of 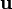 to the head of
to the head of 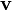 is
is 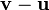 , and vice versa. Note that
, and vice versa. Note that 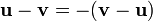 .
.
Of a point from a point
A vector can be considered the difference between two points, or the translation required to take one point onto the other. Given the two points 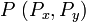 and
and 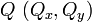 , the vector from
, the vector from  to
to  is
is ![[Q_x-P_x,Q_y-P_y]](/wiki/images/math/0/9/9/099850d0c26a9c2728cb4e8bf7cc205b.png) , and vice versa. Note that
, and vice versa. Note that 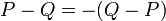 .
.
Multiplication
A vector can be scaled by a scalar (real number). This operation is known as scalar multiplication. The product ![\alpha[v_x,v_y]](/wiki/images/math/4/a/7/4a7a7afccd46a42dd6c3bd932c344913.png) denotes the vector
denotes the vector ![[\alpha v_x,\alpha v_y]](/wiki/images/math/a/e/9/ae98b114463962d1629fa12bb846eb25.png) . This could also be notated
. This could also be notated ![[v_x,v_y]\alpha](/wiki/images/math/b/5/8/b5866d4682b5e7fe484d1ad613aac1b7.png) , though placing the scalar after the vector is more rare. Scalar multiplication takes precedence over addition and subtraction. The geometric interpretation is a bit tricky. If
, though placing the scalar after the vector is more rare. Scalar multiplication takes precedence over addition and subtraction. The geometric interpretation is a bit tricky. If 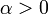 , then the direction of the vector is left unchanged and the length is scaled by the factor
, then the direction of the vector is left unchanged and the length is scaled by the factor 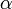 . If
. If 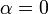 , then the result is the zero vector; and if
, then the result is the zero vector; and if 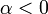 , then the vector is scaled by the factor
, then the vector is scaled by the factor 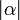 and its direction is reversed. The scalar 1 is the multiplicative identity. Multiplying by the scalar -1 yields the negative of the original vector. Scalar multiplication is distributive.
and its direction is reversed. The scalar 1 is the multiplicative identity. Multiplying by the scalar -1 yields the negative of the original vector. Scalar multiplication is distributive.
The zero vector is a scalar multiple of any other vector. However, if two non-zero vectors are multiples of each other, then either they are parallel, that is, in the same direction (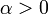 ), or they are antiparallel, that is, in opposite directions (
), or they are antiparallel, that is, in opposite directions (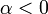 ).
).
Division
A vector can be divided by a scalar 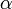 by multiplying it by
by multiplying it by 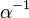 . This is notated in the same way as division with real numbers. Hence,
. This is notated in the same way as division with real numbers. Hence, ![\frac{[x,y]}{\alpha} = \left[\frac{x}{\alpha},\frac{y}{\alpha}\right]](/wiki/images/math/1/d/4/1d4f3d6a70d5ff243d7deecb60c31642.png) . Division by 0 is illegal.
. Division by 0 is illegal.
The unit vector
To every vector except 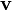 (except
(except 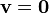 ), we can assign a vector
), we can assign a vector 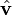 that has the same direction but a length of exactly 1. This is called a unit vector. The unit vector can be calculated as follows:
that has the same direction but a length of exactly 1. This is called a unit vector. The unit vector can be calculated as follows:
There are two elementary unit vectors: [1,0], denoted 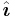 , and [0,1], denoted
, and [0,1], denoted 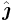 . That is, the unit vectors pointing along the positive x- and y-axes. Note that we can write a vector
. That is, the unit vectors pointing along the positive x- and y-axes. Note that we can write a vector 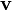 as
as 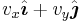 .
.
Obtaining a vector of a given length in the same direction as a given vector
Suppose we want a vector of length  pointing in the same direction as
pointing in the same direction as 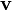 . Then, all we need to do is scale
. Then, all we need to do is scale 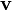 by the factor
by the factor 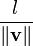 . Thus our new vector is
. Thus our new vector is
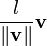 , which can also be written
, which can also be written 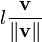 =
= 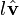 . Hence the unit vector is a "prototype" for vectors of a given direction.
. Hence the unit vector is a "prototype" for vectors of a given direction.
Rotation
Given a vector ![\mathbf{v}\ [x,y]](/wiki/images/math/9/6/3/963672b42fa7dcc6af5c00bc63fd0634.png) and an angle
and an angle 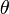 , we can rotate
, we can rotate 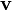 counterclockwise through the angle
counterclockwise through the angle 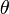 to obtain a new vector
to obtain a new vector ![[x',y']](/wiki/images/math/7/6/b/76b840f1d93f20893e4cb6cce4fce8de.png) using the following formulae:
using the following formulae:
The same formula can be used to rotate points, when they are considered as the endpoints of vectors with their tails at the origin.
Dot product
The dot product or scalar product is notated and defined as follows:
It is commutative, but not associative (since expressions like 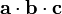 are meaningless). However, the dot product does associate with scalar multiplication; that is,
are meaningless). However, the dot product does associate with scalar multiplication; that is, 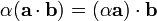 . It is distributive over addition, so that
. It is distributive over addition, so that 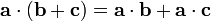 . (This is actually left-distributivity, but right-distributivity follows from the commutative property.) These properties can easily be proven using the Cartesian components. The dot product has two useful properties.
. (This is actually left-distributivity, but right-distributivity follows from the commutative property.) These properties can easily be proven using the Cartesian components. The dot product has two useful properties.
First, the dot product satisfies the relation
where 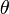 is the angle between
is the angle between 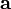 and
and  . This allows us to find the angle between two vectors as follows:
. This allows us to find the angle between two vectors as follows:
This formula breaks down if one of the vectors is the zero vector (in which case no meaningful angle can be defined anyway). The dot product gives a quick test for perpendicularity: two nonzero vectors are perpendicular if and only if their dot product is zero. The dot product is maximal when the two vectors are parallel, and minimal (maximally negative) when the two vectors are antiparallel.
Second, the dot product can be used to compute projections.
The vector projection
The vector projection of  onto
onto  is, intuitively, the "shadow" cast by
is, intuitively, the "shadow" cast by 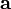 onto
onto  by a light source delivering rays perpendicular to
by a light source delivering rays perpendicular to  . We imagine
. We imagine  to be a screen and
to be a screen and 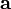 to be an arrow; we are projecting the arrow onto the screen. (It is okay for parts of the projection to lie outside the "screen".) Geometrically, the tail of the projection of
to be an arrow; we are projecting the arrow onto the screen. (It is okay for parts of the projection to lie outside the "screen".) Geometrically, the tail of the projection of 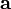 onto
onto  is the foot of the perpendicular from the tail of
is the foot of the perpendicular from the tail of 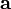 to
to  , and the head of the projection is likewise the foot of the perpendicular from the head of
, and the head of the projection is likewise the foot of the perpendicular from the head of 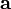 . The vector projection is a vector pointing in the same direction as
. The vector projection is a vector pointing in the same direction as  . There is no standard notation for vector projection; one notation is
. There is no standard notation for vector projection; one notation is 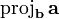 for the projection of
for the projection of 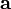 onto
onto  , and vice versa.
, and vice versa.
The scalar projection
The scalar projection is the directed length of the vector projection. That is, if the angle between 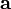 and
and  is acute, then
is acute, then 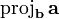 points in the same direction as
points in the same direction as  , and it has a positive directed length; here the scalar projection simply equals the length of the vector projection. If that angle is obtuse, on the other hand, then
, and it has a positive directed length; here the scalar projection simply equals the length of the vector projection. If that angle is obtuse, on the other hand, then 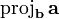 and
and  point in opposite directions, and the scalar projection is the negative of the length of the vector projection. (If the two vectors are perpendicular, the scalar projection is zero.) There is also no standard notation for the scalar projection; one possibility is
point in opposite directions, and the scalar projection is the negative of the length of the vector projection. (If the two vectors are perpendicular, the scalar projection is zero.) There is also no standard notation for the scalar projection; one possibility is 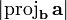 . (Note the single vertical bars, instead of the double vertical bars that denote length.) You have already encountered scalar projections: in the unit circle, the sine of an angle is the scalar projection of a ray making that directed angle with the positive x-axis onto the y-axis, and likewise the cosine is a scalar projection onto the x-axis.
. (Note the single vertical bars, instead of the double vertical bars that denote length.) You have already encountered scalar projections: in the unit circle, the sine of an angle is the scalar projection of a ray making that directed angle with the positive x-axis onto the y-axis, and likewise the cosine is a scalar projection onto the x-axis.
Computing projections
Why have we left discussion of the computation of the scalar and vector projections out of their respective sections? The answer is that the scalar projection is easier to compute, but harder to explain. Place the vectors 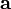 and
and  tail-to-tail at the origin. Now rotate both vectors so that
tail-to-tail at the origin. Now rotate both vectors so that  points to the right. (Rotation actually changes the vectors, of course, but does not change the scalar projection.) Now, the cosine of the angle
points to the right. (Rotation actually changes the vectors, of course, but does not change the scalar projection.) Now, the cosine of the angle 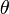 between
between 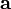 and
and  is the scalar projection of
is the scalar projection of 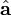 onto
onto  , from the definition of the cosine function. By similar triangles,
, from the definition of the cosine function. By similar triangles, 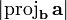 is
is 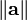 times this. Therefore we find:
times this. Therefore we find:
and vice versa. We could also write this as
because the dot product associates with scalar multiplication.
To compute a vector projection, we notice that we need a vector with the directed length 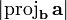 along
along  . This is accomplished by scaling the unit vector
. This is accomplished by scaling the unit vector 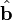 by the value of the scalar projection:
by the value of the scalar projection:
We could also write this as
Two notes: first, projecting onto the zero vector is meaningless since it has no direction, and second, neither scalar nor vector projection is commutative.
Determinant
The determinant of two vectors 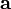 and
and  , denoted
, denoted 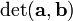 , is the determinant of the matrix having
, is the determinant of the matrix having 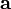 and
and  as rows (or, equivalently, columns), that is:
as rows (or, equivalently, columns), that is:
and is therefore equal to 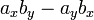 .
The size-2 determinant is often mistakenly referred to as the cross product. (This usage is nearly universal in casual programming parlance and less reputable websites.) This is because there exists a product of two three-dimensional vectors known as the cross product, and the cross-product of two vectors lying in the xy-plane is a vector pointing along the z-axis with z-component equal to the determinant of the two plane vectors. However, no background with three-dimensional vectors, cross-products, or matrices is required for this section. In two dimensions, all that is needed is the formula:
.
The size-2 determinant is often mistakenly referred to as the cross product. (This usage is nearly universal in casual programming parlance and less reputable websites.) This is because there exists a product of two three-dimensional vectors known as the cross product, and the cross-product of two vectors lying in the xy-plane is a vector pointing along the z-axis with z-component equal to the determinant of the two plane vectors. However, no background with three-dimensional vectors, cross-products, or matrices is required for this section. In two dimensions, all that is needed is the formula: 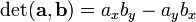 . However, for the sake of convenience, we shall denote the size-2 determinant by the same symbol as the cross product, the cross: hence
. However, for the sake of convenience, we shall denote the size-2 determinant by the same symbol as the cross product, the cross: hence 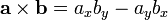 . (This also avoids confusion with the larger matrices in advanced linear algebra and higher dimensions.) It is anticommutative, meaning that
. (This also avoids confusion with the larger matrices in advanced linear algebra and higher dimensions.) It is anticommutative, meaning that 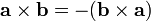 . It satisfies the properties
. It satisfies the properties 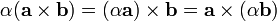 , and with addition it is both left-distributive, so that
, and with addition it is both left-distributive, so that 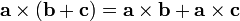 , and right-distributive, so that
, and right-distributive, so that 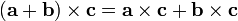 . There are two primary uses for the size-2 determinant in two-dimensional computational geometry.
. There are two primary uses for the size-2 determinant in two-dimensional computational geometry.
The determinant is useful in several algorithms for computing the convex hull because it allows us to determine the directed angle from one vector to another. (Note that the dot product allows us to determine the undirected angle; it makes sense because the dot product commutes whereas the size-2 determinant anticommutes.) The following relation holds:
where 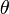 is the directed angle from
is the directed angle from 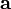 to
to  . That is, the counterclockwise angle from
. That is, the counterclockwise angle from 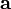 to
to  when they are both anchored at the same point. Rearranging allows us to compute the angle directly:
when they are both anchored at the same point. Rearranging allows us to compute the angle directly:
(Note that the sine function is odd, so that when 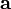 and
and  are interchanged in the above, the right side is negated, and so is the left.)
Often, however, we do not need the directed angle itself. In the monotone chains algorithm for convex hull computation, for example, all we need to know is whether there is a clockwise or a counterclockwise turn from
are interchanged in the above, the right side is negated, and so is the left.)
Often, however, we do not need the directed angle itself. In the monotone chains algorithm for convex hull computation, for example, all we need to know is whether there is a clockwise or a counterclockwise turn from 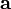 to
to  . (That is, if one wishes to rotate
. (That is, if one wishes to rotate 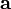 through no more than 180 degrees either clockwise or counterclockwise so that its direction coincides with that of
through no more than 180 degrees either clockwise or counterclockwise so that its direction coincides with that of  , which direction should one choose?) It turns out that if
, which direction should one choose?) It turns out that if 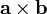 is positive, the answer is counterclockwise; if it is negative, clockwise, and if it is zero, the vectors are either parallel or antiparallel. (Indeed, the closer
is positive, the answer is counterclockwise; if it is negative, clockwise, and if it is zero, the vectors are either parallel or antiparallel. (Indeed, the closer 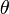 is to a right angle, the larger the cross product in magnitude; in some sense then it measures "how far away" the vectors are from each other.)
is to a right angle, the larger the cross product in magnitude; in some sense then it measures "how far away" the vectors are from each other.)
The determinant is also useful in computing areas of parallelograms and triangles. If the two vectors 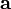 and
and  are placed tail-to-tail, a parallelogram can be formed using these vectors as adjacent sides; its area is
are placed tail-to-tail, a parallelogram can be formed using these vectors as adjacent sides; its area is 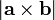 . A triangle can also be formed using these vectors as adjacent sides; its area is half that of the parallelogram, or
. A triangle can also be formed using these vectors as adjacent sides; its area is half that of the parallelogram, or 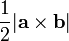 . (This echoes the formula
. (This echoes the formula 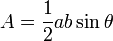 taught in high-school math classes.) In fact, the area of a general quadrilateral
taught in high-school math classes.) In fact, the area of a general quadrilateral 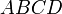 can be computed with a determinant as well; it equals
can be computed with a determinant as well; it equals 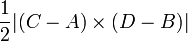 .
.
Circles
Introduction to circles
A circle is the locus of points in the plane equidistant from a given point. That is, we choose some point 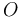 , the centre, and some distance
, the centre, and some distance 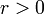 , the radius, and the circle consists exactly of those points whose Euclidean distance from
, the radius, and the circle consists exactly of those points whose Euclidean distance from 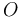 is exactly
is exactly  . When storing a circle in memory, we store merely the centre and the radius.
. When storing a circle in memory, we store merely the centre and the radius.
Equation of a circle
Suppose the circle has centre 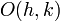 and radius
and radius  . Then, from the definition, we know that any point
. Then, from the definition, we know that any point 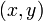 on the circle must satisfy
on the circle must satisfy 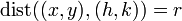 . This means
. This means 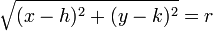 , or
, or 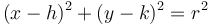 .
.
Inside, outside, or on the circle
The equation of a circle is a sufficient and necessary condition for a point to be on the circle. If it is not on the circle, it must be either inside the circle or outside the circle. It will be inside the circle when its distance from the centre is less than  , or
, or 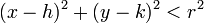 , and similarly it will be outside the circle when
, and similarly it will be outside the circle when 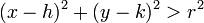 .
.
Intersection of a circle with a line
To determine points of intersection of a circle with another figure (it might also be a circle), solve the simultaneous equations obtained in  and
and 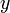 . For example, given a circle centered at (2,3) with radius 2, and the line
. For example, given a circle centered at (2,3) with radius 2, and the line 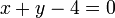 , we would solve the simultaneous equations
, we would solve the simultaneous equations 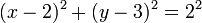 and
and 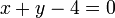 . If there are multiple solutions, each is a different point of intersection; if there are no solutions then the two figures do not intersect. Here then are general results. Note that if you do not check the "no intersection" condition beforehand and plunge straight into the quadratic formula (after reducing the two simultaneous equations to one equation), you will try to extract the square root of a negative number, which will crash some languages (such as Pascal).
. If there are multiple solutions, each is a different point of intersection; if there are no solutions then the two figures do not intersect. Here then are general results. Note that if you do not check the "no intersection" condition beforehand and plunge straight into the quadratic formula (after reducing the two simultaneous equations to one equation), you will try to extract the square root of a negative number, which will crash some languages (such as Pascal).
No points of intersection
When the closest distance from the centre of the circle to the line is greater than the radius of the circle, the circle and line do not intersect. (The formula for the distance from a point to a line can be found in the Lines section of this article.)
One point of intersection
When the closest distance from the centre of the circle to the line is exactly the circle's radius, the line is tangent to the circle. One way of finding this point of tangency, the single point of intersection, is to drop a perpendicular from the centre of the circle to the line. (The technique for doing so is found in the Lines section.) This will, of course, yield the same answer as solving the simultaneous equations.
Two points of intersection
When the closest distance from the centre of the circle to the line is less than the circle's radius, the line intersects the circle twice.
To find the two points of intersection, first drop a perpendicular from the centre of the circle to the line. Call the foot of the perpendicular  and denote the distance
and denote the distance 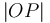 by
by 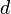 . Now, let the two points of intersection be
. Now, let the two points of intersection be 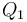 and
and 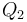 . Then, the triangles
. Then, the triangles 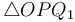 and
and 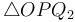 are right-angled, and hence we see that
are right-angled, and hence we see that 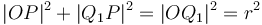 and
and 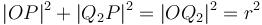 . So we compute the value
. So we compute the value 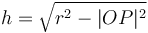 ; now, if we move
; now, if we move 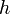 units in either direction along the line from
units in either direction along the line from  , we will reach either
, we will reach either 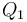 or
or 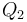 . (The technique to do so is given in section Translation along a line.)
. (The technique to do so is given in section Translation along a line.)
Intersection of a circle with a circle
Finding the points of intersection of two circles follows the same basic idea as the circle-line intersection. Here's how to determine the nature of the intersection beforehand, to avoid accidentally trying to take the square root of a negative number:
No points of intersection
When the distance between the centres of the circles is less than the difference between their radii, the circle with smaller radius will be contained completely within the circle of larger radius. When the distance between the centres of the circles is greater than the sum of their radii, neither circle will be inside the other, but still the two will not intersect.
One point of intersection
Let the two circles have centres 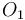 and
and 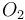 and radii
and radii 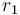 and
and 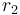 .
.
- When the distance between the centres of the circles is exactly the difference between their radii, the two circles will be internally tangent. Suppose that the first circle is larger. Then the point of intersection lies on the line between
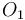 and
and 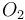 . The intersection point and
. The intersection point and  are on opposite sides of
are on opposite sides of 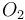 , and its distances from
, and its distances from 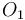 and
and 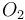 are
are 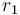 and
and 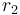 , respectively. This gives
, respectively. This gives 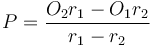 . (It turns out that if we swap the 1's and 2's in this formula, we get the same value; hence we can use this formula without regard to which circle is labelled 1 and which one is 2.)
. (It turns out that if we swap the 1's and 2's in this formula, we get the same value; hence we can use this formula without regard to which circle is labelled 1 and which one is 2.) - When the distance between the centres of the circles is exactly the sum of their radii, they will be externally tangent; they will have one point of intersection located between
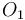 and
and 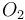 ; it will be
; it will be 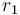 units away from the former and
units away from the former and 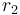 units away from the latter, giving the formula
units away from the latter, giving the formula 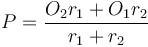 .
.
Two points of intersection
In all other cases, there will be two points of intersection.
To find them, it will be helpful to draw a diagram. Denote the centres of the circles 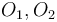 , their radii
, their radii 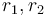 , and the two points of intersection
, and the two points of intersection 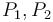 . First draw the radical axis, the line that passes through
. First draw the radical axis, the line that passes through 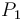 and
and 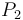 . This passes through the midpoint
. This passes through the midpoint 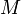 between
between 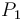 and
and 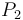 , and here it intersects perpendicularly the line between
, and here it intersects perpendicularly the line between 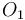 and
and 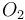 . Denote
. Denote 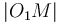 and
and 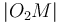 by
by 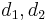 , respectively. Clearly
, respectively. Clearly
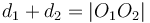 . (1)
. (1)
Also, from the Pythagorean theorem, 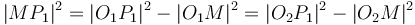 , or
, or 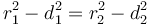 . Rearranging this gives
. Rearranging this gives
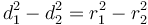 . (2)
. (2)
Now we solve for 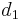 and
and 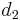 . To do this, we factor the left side of (2), giving
. To do this, we factor the left side of (2), giving 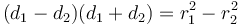 , which allows us to divide through by (1), thus obtaining
, which allows us to divide through by (1), thus obtaining
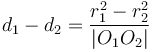 . (3)
. (3)
Equations (1) and (3) are linear and may be used to solve for 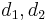 in a straightforward fashion.
in a straightforward fashion.
Now we can compute the coordinates of 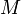 as
as 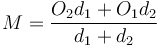 , using the argument from the previous section. Then construct the line perpendicular to
, using the argument from the previous section. Then construct the line perpendicular to 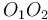 that passes through
that passes through 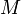 (the radical axis). Finally, we can find the distance
(the radical axis). Finally, we can find the distance 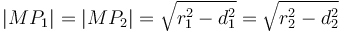 , and move this distance in either direction along the radical axis (see Translation along a line) to obtain
, and move this distance in either direction along the radical axis (see Translation along a line) to obtain  and
and  .
.
It should be noted that two circles that intersect at two points cut each other into two arcs each: one arc that lies within the other circle, and one that lies outside it. It is not immediately obvious which is which. However, you should be able to convince yourself from drawing a diagram that if 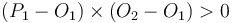 , then the arc of the first circle that is inside the second circle is counterclockwise from
, then the arc of the first circle that is inside the second circle is counterclockwise from  to
to  , but if that determinant is negative, then the inside arc is counterclockwise from
, but if that determinant is negative, then the inside arc is counterclockwise from  to
to 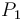 . (For an example of where this is important, see Detectors.)
. (For an example of where this is important, see Detectors.)
Tangents
A line is said to be tangent to a circle if it intersects the circle at exactly one point.
The tangent has an important property: if a circle with centre 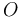 has a tangent line
has a tangent line  that touches it at
that touches it at  , then
, then 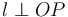 . The proof of this fact is simple: we assume that the two lines are not perpendicular, then drop a perpendicular from
. The proof of this fact is simple: we assume that the two lines are not perpendicular, then drop a perpendicular from 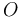 to
to  at
at  . We observe that
. We observe that 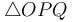 is right-angled at
is right-angled at  , and that therefore
, and that therefore 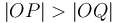 . But this implies that
. But this implies that  is inside the circle, a contradiction.
is inside the circle, a contradiction.
To actually find the tangent line to one circle at a given point on its circumference is easy; it is simply the line passing through that point that is perpendicular to the radius.
From point to circle
Sometimes we may also be given a circle with centre and radius 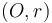 plus a point
plus a point  and asked to find a tangent to the circle that passes through the point. There may be either zero, one, or two such tangents.
and asked to find a tangent to the circle that passes through the point. There may be either zero, one, or two such tangents.
Point is inside circle
When the point is inside the circle, there are no tangents to the circle through that point, because any line through the point must intersect the circle twice.
Point is on circle
When the point is on the circumference of the circle, the line passing through  that is perpendicular to
that is perpendicular to  is the unique tangent to the circle passing through that point.
is the unique tangent to the circle passing through that point.
Point is outside circle
When the point is outside the circle, there are two tangents to the circle passing through the point. To construct one such tangent, we use a trick called inversion. We let one of the points of tangency be denoted  . Now
. Now  is right-angled at
is right-angled at  . If we now drop a perpendicular from
. If we now drop a perpendicular from  to
to 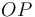 at
at 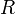 , we obtain triangle
, we obtain triangle  which is similar to
which is similar to 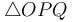 . This means that
. This means that 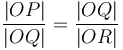 , so
, so 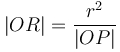 . Note that
. Note that  is inside the circle, unlike
is inside the circle, unlike  which is outside (hence the name inversion.) This allows us to locate point
which is outside (hence the name inversion.) This allows us to locate point 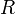 on the line segment
on the line segment 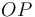 . Then, we see that the line segment
. Then, we see that the line segment 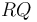 is perpendicular to
is perpendicular to 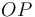 and has length
and has length 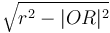 from the Pythagorean theorem in
from the Pythagorean theorem in  . This gives us enough information to compute the coordinates of
. This gives us enough information to compute the coordinates of  . There will be two possibilities, since we can draw two rays through
. There will be two possibilities, since we can draw two rays through 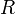 that are perpendicular to
that are perpendicular to 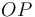 .
.
Circle-circle tangents
A pair of circles may have either zero, one, two, three, or four mutual tangents.
Zero mutual tangents
If one circle lies within the other (that is, the difference between their radii is greater than the distance between their centres), then they have no mutual tangents, since every tangent to the outer circle lies outside it, and hence cannot touch the inner circle.
One mutual tangent
Two circles will have one mutual tangent if they are internally tangent (that is, the difference between their radii equals the distance between their centres). This tangent can easily be found after constructing the point  of internal tangency (see section One point of intersection above).
of internal tangency (see section One point of intersection above).
Two mutual tangents
A pair of circles that intersect at two points has two mutual tangents, one on either "side". We will consider the problem of how to determine one of them.
Assume the circles have centres 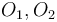 and radii
and radii 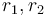 . Assume further that they have some mutual tangent
. Assume further that they have some mutual tangent  and that
and that  is tangent to the circles at
is tangent to the circles at 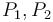 , respectively. We see that
, respectively. We see that 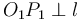 and
and 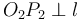 . Now, assume without loss of generality that
. Now, assume without loss of generality that 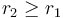 . Then drop the perpendicular from
. Then drop the perpendicular from  to
to  at
at  , and obtain
, and obtain 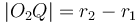 . Then
. Then 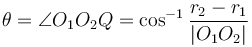 . Also, we can solve for
. Also, we can solve for 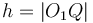 using the Pythagorean theorem, obtaining
using the Pythagorean theorem, obtaining 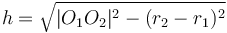 . Notice that because
. Notice that because 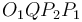 is a rectangle,
is a rectangle, 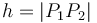 .
.
There are two possibilities for the location of 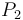 . One of them is obtained by rotating the ray
. One of them is obtained by rotating the ray 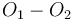 clockwise through angle
clockwise through angle 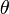 , the other obtained by rotating it counterclockwise, and in either case determining where the ray cuts the second circle. (So it doesn't actually matter which circle is bigger; the formula
, the other obtained by rotating it counterclockwise, and in either case determining where the ray cuts the second circle. (So it doesn't actually matter which circle is bigger; the formula 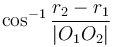 will give the same result up to sign.)
will give the same result up to sign.)
We can then argue that the coordinates of one of the possible  's is given by
's is given by ![O_2 + r_2 [\cos (\operatorname{atan2}(O_1-O_2) + \theta), \sin (\operatorname{atan2}(O_1-O_2) + \theta)]](/wiki/images/math/b/0/b/b0bc8c6514a8dc91a3291cd4eace2859.png) , because
, because 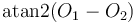 represents the directed angle from the positive x-axis to the ray from
represents the directed angle from the positive x-axis to the ray from 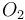 to
to 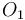 , and we are adding onto this directed angle the value
, and we are adding onto this directed angle the value 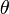 to get our final position. The other possible
to get our final position. The other possible 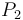 will be given by subtracting
will be given by subtracting 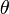 instead of adding.
instead of adding.
This formula as written is slow, since it involves trigonometric functions, which have a higher invisible constant factor than algebraic operations and square roots. Therefore, we will rewrite it in terms of only algebraic operations. Define 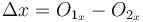 and
and 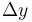 analogously.
analogously.
Verify the identities 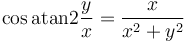 and
and 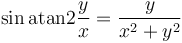 . (These are actually obvious from the definition of
. (These are actually obvious from the definition of atan2). Then:
And likewise
After locating  , we just construct the line passing through
, we just construct the line passing through  that is perpendicular to
that is perpendicular to  and this will also be tangent to the first circle at
and this will also be tangent to the first circle at 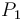 .
.
Three mutual tangents
The case of three mutual tangents occurs when the two circles are externally tangent that is, when the sum of their radii equals the distance between their centres. In this case two of the three tangents (the "outer" ones) can be found using the formula in the previous section, and the third, which passes "between" the circles, may easily be found by first finding the point of mutual tangency (see section One point of intersection above).
Four mutual tangents
If two circles do not intersect or overlap at all, that is, the distance between their centres is greater than the sum of their radii, they will have four mutual tangents. Two of the mutual tangents can be found using the formulas two sections above. These are the two "outer" tangents, with the property that both circles lie on the same side of an outer tangent. There are also two "inner" tangents that "separate" the two circles from each other.
The procedure for computing these "inner" tangents is similar to the procedure for computing the "outer" tangents. We begin by letting  be one of these tangents, that touches the first circle at
be one of these tangents, that touches the first circle at 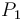 and the second at
and the second at 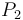 . Let the point of intersection of
. Let the point of intersection of  with
with 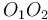 be denoted
be denoted  . Then, right-angled
. Then, right-angled 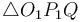 is similar to right-angled
is similar to right-angled 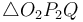 . Let
. Let 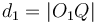 and
and 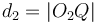 . Then, by similarity, we see that
. Then, by similarity, we see that 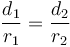 . Along with the equation
. Along with the equation 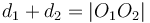 , we can solve:
, we can solve: 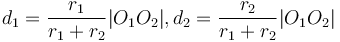 . Then, letting
. Then, letting 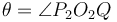 , we have
, we have 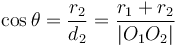 . Let
. Let 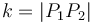 , and see that
, and see that 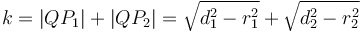 , which, after some messy algebra, will turn out to be
, which, after some messy algebra, will turn out to be 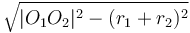 . Also observe that
. Also observe that 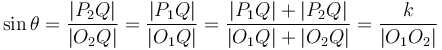 .
.
Moving along, we have ![P_2 = O_2 + r_2 [\cos (\operatorname{atan2}(O_1-O_2) + \theta), \sin (\operatorname{atan2}(O_1-O_2) + \theta)]](/wiki/images/math/a/d/5/ad5a0dc6227616f3da3bdafeedaa7553.png) as before. Defining
as before. Defining 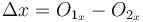 and
and 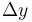 analogously, we obtain:
analogously, we obtain:
and likewise
Careful! The value of 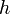 in this case is not the same as the value of
in this case is not the same as the value of 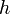 for the outer tangents.
for the outer tangents.
Summary and discussion
We will summarize the results below. (Note that we have exchanged the two circles.) We define 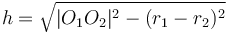 and
and 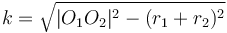 , and then the points of tangency of the two outer tangents with the first circle are given by:
, and then the points of tangency of the two outer tangents with the first circle are given by:
and likewise for the two inner tangents:
The first pair of formulas will be invalid when 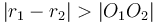 , because
, because 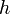 will be undefined. Obviously, in this case,
will be undefined. Obviously, in this case, 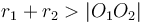 also, so
also, so 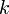 will also be undefined, and the second pair of formulas will be invalid.
will also be undefined, and the second pair of formulas will be invalid.
When 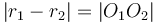 , we will obtain
, we will obtain 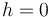 , so
, so 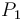 and
and 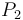 will coincide. The second pair of formulas will still be invalid, so we will obtain a total of one point of tangency.
will coincide. The second pair of formulas will still be invalid, so we will obtain a total of one point of tangency.
When 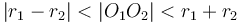 , we will obtain
, we will obtain 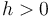 , so
, so 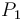 and
and 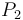 will be distinct, but
will be distinct, but 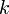 will still be undefined, so we obtain a total of two points of tangency.
will still be undefined, so we obtain a total of two points of tangency.
When 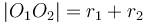 , we will obtain
, we will obtain 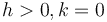 giving two distinct points
giving two distinct points  , but
, but  , a total of three points of tangency.
, a total of three points of tangency.
Finally, when 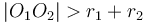 , then
, then 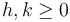 and all four points
and all four points  will be distinct, as expected.
will be distinct, as expected.
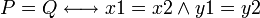
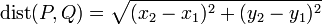
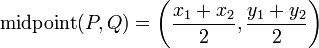
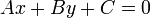
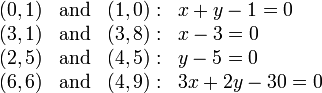
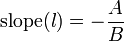
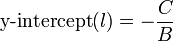
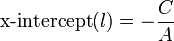
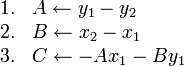
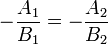
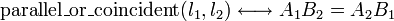
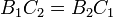
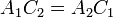
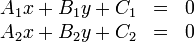
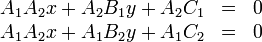
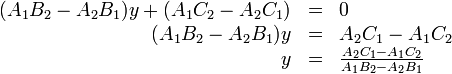
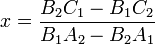
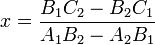
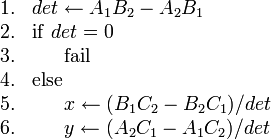
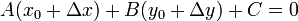
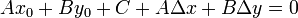
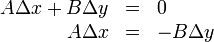
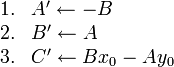
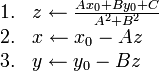
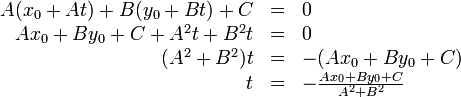
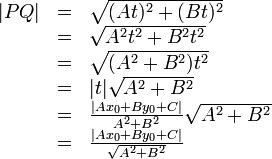
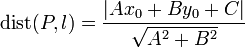
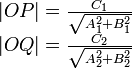
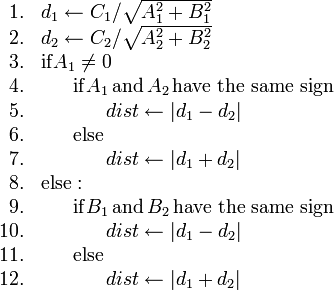
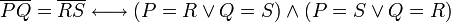
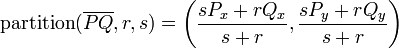
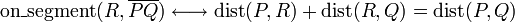
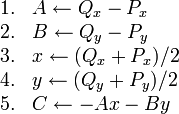
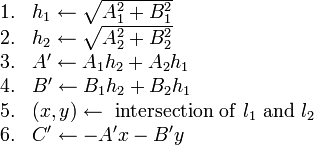
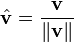
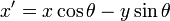
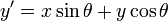
![[a_x,a_y]\cdot[b_x,b_y] = a_x b_x + a_y b_y](/wiki/images/math/0/5/6/05604337d6518ed50fd18e7cce34fe60.png)
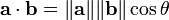
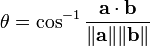
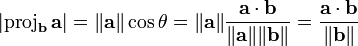
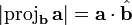
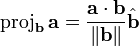
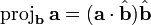
![\left[\begin{matrix} a_x & a_y \\ b_x & b_y \end{matrix}\right]](/wiki/images/math/d/8/6/d8610e3ba914cee033989369ffb432bd.png)
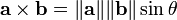
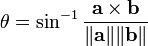
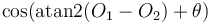
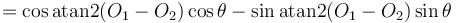
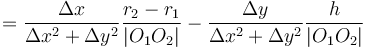
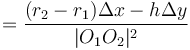
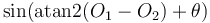
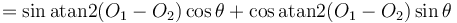
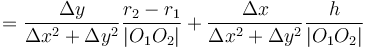
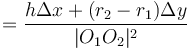
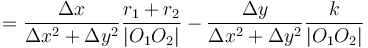
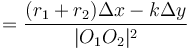
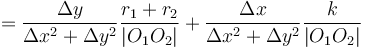
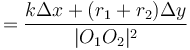
![P_1 = O_1 + \frac{r_1}{|O_1O_2|^2} [(r_1-r_2)\Delta x - h\Delta y, h\Delta x + (r_1-r_2)\Delta y]](/wiki/images/math/3/3/3/333bd1e6ae534be6cf9fcbffd1b588d0.png)
![P_2 = O_1 + \frac{r_1}{|O_1O_2|^2} [(r_1-r_2)\Delta x + h\Delta y, -h\Delta x + (r_1-r_2)\Delta y]](/wiki/images/math/b/f/b/bfb3426c198e578b9f6b5b45ffa25464.png)
![P_3 = O_1 + \frac{r_1}{|O_1O_2|^2} [(r_1+r_2)\Delta x - k\Delta y, k\Delta x + (r_1+r_2)\Delta y]](/wiki/images/math/d/7/e/d7e462fb3ae839a0d8fed852ab74ccd5.png)
![P_4 = O_1 + \frac{r_1}{|O_1O_2|^2} [(r_1+r_2)\Delta x + k\Delta y, -k\Delta x + (r_1+r_2)\Delta y]](/wiki/images/math/e/b/2/eb2f89e9833d27f049e79f1ac97f272f.png)