All nearest smaller values
In a list of numbers  , the nearest smaller value (NSV) to an entry
, the nearest smaller value (NSV) to an entry 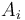 is the last entry preceding it with a smaller value, if any; that is, the entry
is the last entry preceding it with a smaller value, if any; that is, the entry  with greatest
with greatest 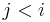 such that
such that 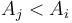 . The all nearest smaller values (ANSV) problem is that of computing the NSV for each number in the list.
. The all nearest smaller values (ANSV) problem is that of computing the NSV for each number in the list.
Algorithm
It is obvious that, upon seeing the list for the first time, we cannot guarantee being able to find the NSV to a given entry in less than linear time, because it could be any of the preceding entries in the list, and thus, in the worst case, we must examine all of them. If we do a linear scan on each element, we get a trivial 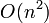 time solution to ANSV.
time solution to ANSV.
However, it turns out that there is a simple linear time (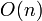 ) solution to ANSV, which is clearly asymptotically optimal, since the size of the output is
) solution to ANSV, which is clearly asymptotically optimal, since the size of the output is 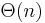 anyway. To understand this algorithm, we make a series of observations and refinements:
anyway. To understand this algorithm, we make a series of observations and refinements:
- If
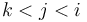 , then it is only possible for
, then it is only possible for 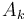 to be a NSV for
to be a NSV for 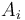 if
if 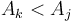 ; otherwise
; otherwise  will always be both smaller and "nearer".
will always be both smaller and "nearer". - Thus, if we scan the list from left to right, and compute the NSV for each element as we visit it, and we encounter
 such that
such that 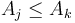 for some
for some 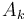 already seen, then we can pretend that
already seen, then we can pretend that 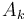 doesn't exist anymore.
doesn't exist anymore. - Given this fact, the only entries we've seen so far that we need to keep track of are the ones that are less than all following entries seen so far.
- This means that the list of "retained" entries is monotonically increasing.
- Once we get to
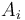 , we can compute its NSV by looking backward though the list of retained previous entries, selecting the first one we find that is less than
, we can compute its NSV by looking backward though the list of retained previous entries, selecting the first one we find that is less than 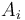 . Also, all the retained entries skipped along the way—the ones that are greater than or equal to
. Also, all the retained entries skipped along the way—the ones that are greater than or equal to 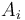 —can now be discarded.
—can now be discarded.
In these five points the essence of the algorithm is contained. We can use a stack to store the list of previously seen values that are being retained, because we only add to and remove from it at the end. As an implementation detail, in step 5, it is useful to have a sentinel, so that we don't try to pop off an empty stack (when 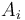 has no preceding smaller value).
has no preceding smaller value).
Pseudocode:
input array A[1..n]
let A[0] ← -∞
let S be an empty stack
push(S,0)
for i ∈ [1..n]
while A[top(S)] ≥ A[i]
pop(S)
let NSV[i] ← top(S)
push(S,i)
After this code has completed, NSV[i] will contain the index of the NSV of 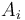 (not the NSV itself).
(not the NSV itself).
Applications
A theoretically important application of ANSV is the construction of the Cartesian tree for a given list of numbers; a node's parent in a Cartesian tree is either its NSV or its NSV in the reversed array (that is, the nearest smaller value on the right rather than on the left), whichever one is larger. (Proof is given in the other article.)
Running ANSV twice, once on an array and once on its reverse, can be used to find, for each element 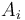 , the range
, the range ![[j,k]](/wiki/images/math/0/4/a/04a572c655742d66ec17d0c4c21d43bb.png) such that
such that 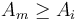 for each
for each ![m \in [j,k]](/wiki/images/math/6/1/0/610b840cf6b25213f83e6b7e2655456a.png) . Geometrically, if the array is taken to represent a histogram in which
. Geometrically, if the array is taken to represent a histogram in which 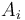 is the height of the ith bar, then this range gives how large a rectangle can be that just touches the top of the ith bar while staying contained within the histogram. This can then trivially be used to find the largest rectangle contained entirely within the histogram.
is the height of the ith bar, then this range gives how large a rectangle can be that just touches the top of the ith bar while staying contained within the histogram. This can then trivially be used to find the largest rectangle contained entirely within the histogram.
This gives an easy linear-time solution to the problem of finding the largest empty axis-aligned rectangle in a rectangular grid (in which each square is either completely full or completely empty): sweep from top to bottom; keep track of how far up one can go along each column until encountering an obstacle, starting from the current row; and find the largest rectangle contained within the corresponding histogram constructed at each row.
Problems
- CCC '11 Stage 2: Biggest (Zero Carbon) Footprint
- Largest rectangle in a histogram
- City Game
- USACO: Rectangular Barn