Equivalence relation
An equivalence relation is a structure imposed on a set that can be interpreted as making some elements equivalent to others. It generalizes the concept of equality and comprises various relationships both in formal mathematics and in real life.
Definition
Given a set  , the binary relation ≡ is an equivalence relation if and only if it satisfies the following three properties:
, the binary relation ≡ is an equivalence relation if and only if it satisfies the following three properties:
- Reflexivity: For any
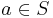 ,
,  .
. - Symmetry: If
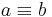 , then
, then  .
. - Transitivity: If
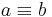 and
and 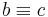 , then
, then  .
.
The first property tells us that every element is equivalent to itself. The second property tells us that equivalence is two-way. The third suggests a grouping structure of equivalent items and is what allows us to use notation such as 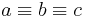 .
.
Examples
The following are sets with equivalence relations:
- Let
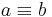 if and only if
if and only if 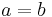 , on any set.
, on any set. - Let
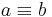 be true no matter what, on any set.
be true no matter what, on any set. - On the set of integers, let
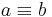 if and only if
if and only if 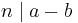 , where
, where 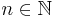 . (This equivalence relation is called congruence, and
. (This equivalence relation is called congruence, and  and
and  are said to be congruent modulo
are said to be congruent modulo  .)
.)
- For example, let two integers be equivalent if and only if they are both even or both odd (here
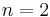 ).
).
- For example, let two integers be equivalent if and only if they are both even or both odd (here
- Let
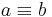 if and only if
if and only if  and
and  are isomorphic (where
are isomorphic (where  and
and  belong to some set on which this makes sense, such as graphs or vector spaces.)
belong to some set on which this makes sense, such as graphs or vector spaces.) - Suppose
 is the set of human beings. Let
is the set of human beings. Let 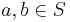 be equivalent if and only if
be equivalent if and only if  and
and  are either the same person or siblings.
are either the same person or siblings. - In a graph
 , let vertices
, let vertices 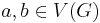 be equivalent if and only if they are reachable from each other.
be equivalent if and only if they are reachable from each other. - Let two days
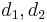 be equivalent if and only if they occurred on the same day of the week.
be equivalent if and only if they occurred on the same day of the week. - Let two configurations of the Rubik's cube be equivalent if and only if it is possible to interconvert them using face rotations. (Note that if a configuration is not equivalent to the solved configuration, it is invalid and unsolvable.)
- Let two matrices be equivalent if and only if they can be interconverted using only elementary row operations. (This is called row equivalence.)
- Let two real-valued functions be equivalent if and only if they differ by a constant. (If the functions are differentiable, then they have the same derivative.)
- Let two infinite bit strings be equivalent if and only if they differ in at most a finite number of positions (i.e., have finite Hamming distance).
- Let two chemical names be equivalent if and only if they name the same compound. (For example, perhydronaphthalene and bicyclo[4.4.0]decane are equivalent.)
- Let two polyhedra be equivalent if and only if it is possible to dissect one of them into a finite number of pieces with straight cuts and reassemble the pieces into the other.
- An already existing equivalence relation, such as equality, on a part or property of an object can be extended to one on the object itself. For example, we can define two people to be equivalent if they are of the same age, or if they were born in the same country, or if they have the same number of children.
The following are not equivalence relations:
- Let two people be equivalent if and only if they speak a common language. This is reflexive and symmetric, but not transitive.
- Let two people be equivalent if and only if they are friends. This is symmetric but it is not transitive (it may be reflexive depending on whether we consider a person to be his/her own friend).
- Let two people be equivalent if and only if they are either the same person, siblings, or half-siblings. This is reflexive and symmetric but not transitive.
- Let two positions of the Rubik's Cube be equivalent if and only if they can be interconverted in a single face turn. This is reflexive and symmetric, but not transitive.
- Let
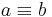 if and only if
if and only if 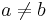 . This is symmetric but neither reflexive nor transitive.
. This is symmetric but neither reflexive nor transitive. - Let
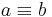 if and only if
if and only if 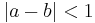 , where
, where 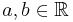 . This is symmetric and reflexive, but not transitive.
. This is symmetric and reflexive, but not transitive. - Let
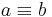 if and only if
if and only if 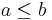 , where
, where 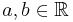 . This is reflexive and transitive, but not symmetric, and is actually a partial order.
. This is reflexive and transitive, but not symmetric, and is actually a partial order. - Let
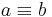 if and only if
if and only if 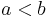 , where
, where 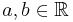 . This is transitive, but neither reflexive nor symmetric.
. This is transitive, but neither reflexive nor symmetric. - Let
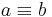 be false no matter what. This is symmetric and transitive, but not reflexive.
be false no matter what. This is symmetric and transitive, but not reflexive.
Equivalence class
Given an equivalence relation  on a set
on a set  , we can partition
, we can partition  into disjoint subsets such that
into disjoint subsets such that 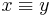 iff
iff  and
and  belong to the same class, and there is exactly one way to do so. The proof of this fact is left as an exercise to the reader. These disjoint subsets are known as equivalence classes. The following are examples:
belong to the same class, and there is exactly one way to do so. The proof of this fact is left as an exercise to the reader. These disjoint subsets are known as equivalence classes. The following are examples:
- If every element in a set is only equivalent to itself, then each equivalence class contains only one element.
- If every element in a set is equivalent to every element, then there is only one equivalence class, and it is the entire set.
- If we use congruence on the set of integers, there are
 equivalence classes, one for each remainder (
equivalence classes, one for each remainder (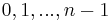 ). So one equivalence class is
). So one equivalence class is 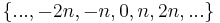 , one is
, one is 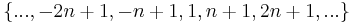 , and so on. (Each equivalence class is infinite.)
, and so on. (Each equivalence class is infinite.)
- In the case
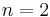 , there are two equivalence classes. One is the set of even integers and one is the set of odd integers.
, there are two equivalence classes. One is the set of even integers and one is the set of odd integers.
- In the case
- If two human beings are equivalent if and only if they are either the same person or siblings, then each equivalence class consists of all children of a given pair of individuals. Some such classes may contain only one person, whereas some may contain more than a dozen.
- In an undirected graph, where the equivalence relation is reachability, each connected component is an equivalence class. In a directed graph, where the equivalence relation is mutual reachability, each strongly connected component is an equivalence class.
- If we let two days be equivalent if and only if they occur on the same day of the week, there are seven equivalence classes. One consists of all Mondays, one of all Tuesdays, and so on.
Invariant
Let a set  be given with equivalence relation
be given with equivalence relation  . An invariant is a function
. An invariant is a function 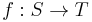 (where
(where  is any set) such that
is any set) such that  if
if 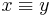 . In the case that an only if relationship also holds, this invariant may be used to check whether two elements are equivalent. The function that maps an element to the equivalence class containing it is an invariant, but the most useful invariant is often the one that distills the essence of what equivalent elements have in common; it is most useful when it is a small number or set of numbers that can be easily compared. Here are examples of suitable invariants:
. In the case that an only if relationship also holds, this invariant may be used to check whether two elements are equivalent. The function that maps an element to the equivalence class containing it is an invariant, but the most useful invariant is often the one that distills the essence of what equivalent elements have in common; it is most useful when it is a small number or set of numbers that can be easily compared. Here are examples of suitable invariants:
- Suppose that we have the integers with the congruence relation modulo
 . An invariant would be the least non-negative residue of an integer, that is, the (positive) remainder obtained upon dividing the integer by
. An invariant would be the least non-negative residue of an integer, that is, the (positive) remainder obtained upon dividing the integer by  .
.
- In the case
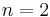 , the invariant of an even integer would be 0, and that of an odd integer 1.
, the invariant of an even integer would be 0, and that of an odd integer 1.
- In the case
- Suppose
 is the set of human beings. Let
is the set of human beings. Let 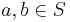 be equivalent if and only if
be equivalent if and only if  and
and  are either the same person or siblings. Then an invariant would be a function
are either the same person or siblings. Then an invariant would be a function 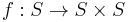 , where
, where 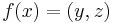 with
with  the biological mother of
the biological mother of  and
and 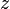 the biological father of
the biological father of  . (This invariant may become obsolete with advances in biotechnology.)
. (This invariant may become obsolete with advances in biotechnology.) - We can use depth-first search or breadth-first search to assign a numerical ID to each connected component in a graph. The function that maps a vertex to the ID of the connected component containing it is a suitable invariant for the mutually reachable equivalence relation.
- Define
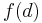 to be 0 if day
to be 0 if day 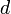 occurs on Monday, 1 if
occurs on Monday, 1 if 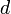 occurs on Tuesday, and so on. This is a suitable invariant for the equivalence relation falling on the same day of the week.
occurs on Tuesday, and so on. This is a suitable invariant for the equivalence relation falling on the same day of the week. - The problem of finding an invariant for determining whether two polyhedra may be interconverted by dissection and reassembly was long-standing. It turns out that the pair
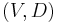 is a suitable invariant, where
is a suitable invariant, where  is the volume of a polyhedron and
is the volume of a polyhedron and 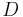 is a quantity named the Dehn invariant after its inventor, Max Dehn.
is a quantity named the Dehn invariant after its inventor, Max Dehn.
In other cases, it may not be easy to find an invariant. For example, there is no obvious invariant for interconvertibility of positions on the Rubik's Cube.
Canonical form
An invariant 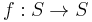 that satisfies
that satisfies  if and only if
if and only if 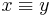 is said to map each element to a canonical form. In other words, the invariant is an element of the set itself. Another way of thinking about this is that we select exactly one element, a representative, from each equivalence class; the invariant is then the function that maps an element to the representative of its equivalence class. Finding the canonical form of an element is known as canonization or canonicalization. Here are examples:
is said to map each element to a canonical form. In other words, the invariant is an element of the set itself. Another way of thinking about this is that we select exactly one element, a representative, from each equivalence class; the invariant is then the function that maps an element to the representative of its equivalence class. Finding the canonical form of an element is known as canonization or canonicalization. Here are examples:
- The invariants given above for congruence modulo
 give canonical forms, since they map
give canonical forms, since they map 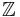 onto a subset of itself.
onto a subset of itself. - Using the are siblings or the same person equivalence relation on humans, a possible canonical form is the oldest sibling of a family. (This may not always be easy to define, if the family has twins, triplets, etc..)
- If we number the vertices of a graph, we can let the representative of each vertex be the lowest-numbered vertex that is in the same connected component. This is a canonical form for the mutual reachability equivalence relation.
- If we are letting two days be equivalent if and only if they occur on the same day of the week, we can use, as a canonical form, the first day on or after January 1, 1970 that occurs on the same day of the week as a given day. Hence there are only seven days in canonical form, that is, the days of the week starting on January 1, 1970.
- The reduced row echelon form of a matrix is a canonical form for the row equivalence equivalence relation.
- Canonization of graphs according to isomorphism and chemical names according to the structures they represent are difficult problems, with much active research in the field.
- When we let
 be
be 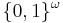 , that is, the set of infinite bit strings, and define two bit strings to be equivalent if and only if they differ at only a finite number of positions, it becomes unclear how we can ever select any representatives at all. If we assume the axiom of choice, then this equivalence relation (and all others) has a canonical form, but it does not tell us how to construct one. (This turns out to be the key to the solution to the uncountably infinite prisoners and hats problem.)
, that is, the set of infinite bit strings, and define two bit strings to be equivalent if and only if they differ at only a finite number of positions, it becomes unclear how we can ever select any representatives at all. If we assume the axiom of choice, then this equivalence relation (and all others) has a canonical form, but it does not tell us how to construct one. (This turns out to be the key to the solution to the uncountably infinite prisoners and hats problem.)