String

The string is one of the most fundamental objects in computer science. Strings are intimately familiar to us in the form of text and therefore it is no wonder that the theory of strings (which is to be distinguished from the field of theoretical physics known as "string theory") is one of the most extensively studied subdisciplines of computer science.

Definitions

An alphabet, usually denoted 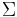$\Sigma$ is a finite nonempty set (whose size is denoted 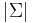$|\Sigma|$). It is often assumed that the alphabet is totally ordered, but this is not always necesary. An element of this the alphabet is known as a character.

The set of 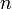$n$-tuples of 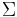$\Sigma$ is denoted 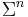$\Sigma^n$. A string of length 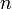$n$ is an element of 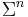$\Sigma^n$. The set 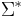$\Sigma^*$ is defined 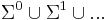$\Sigma^0 \cup \Sigma^1 \cup ...$; an element of 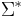$\Sigma^*$ is known simply as a string over 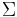$\Sigma$. The empty string, denoted 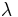$\lambda$, is the unique element of 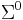$\Sigma^0$. (The usual definition of "string", then, requires strings to have finite but unbounded length.)

For ease of conceptualization, we shall usually assign a symbol, a graphical representation, to each character of the alphabet and, considering a string as a sequence of characters, render it as a sequence of symbols. We shall usually do so in boldface, but in this section we shall use italics to avoid confusion with terms being defined, hence, PEG. On other occasions we may choose to represent them with the ordered list notation, hence, [P,E,G]. (This form is useful when the symbols consist of more than one glyph, as can be the case when they are integers; see below.) We will often number the characters of strings, sometimes starting from zero, sometimes starting from one.

Examples of alphabets include:

• The binary alphabet, with exactly two characters (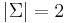$|\Sigma|=2$), usually denoted 0 and 1. In virtually all computers ever built, data are strings over the binary alphabet, and are known as bit strings.
• The Latin alphabet, with the characters a, A, b, B, ..., z, Z (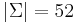$|\Sigma|=52$). English words may be considered strings over the Latin alphabet.
• The Unicode character set (the size of this alphabet depends somewhat on what we consider to be a valid Unicode character). Text files may be considered strings over this alphabet.
• The set of integers 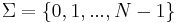$\Sigma = \{0, 1, ..., N-1\}$ for some 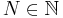$N \in \mathbb{N}$, for which $|\Sigma| = N$. Here the characters are also integers, and their corresponding symbols might have more than one glyph when 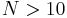$N > 10$. (Recall that the definition of character is broader than the common concept of the character as the smallest, indivisible element of writing.)
• The set of nitrogenous bases in DNA, {A, C, G, T}, with 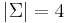$|\Sigma|=4$. Codons are considered members of 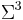$\Sigma^3$, and DNA sequences members of $\Sigma^*$.

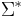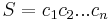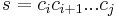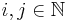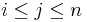A substring of a string $S = c_1 c_2 ... c_n$ is given by $s = c_i c_{i+1} ... c_j$ for some $i, j \in \mathbb{N}$ with $i \leq j \leq n$. Note that the empty string is considered a substring of all other strings. In other words, it is a series of (possibly zero) characters occurring consecutively in a string, taken in order. For example, the, in, here, and therein are all substrings of therein, as is 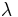$\lambda$; however, tin is not (the characters are not consecutive in the original string), nor is rine (the characters do not occur in order in the original string). A prefix is a substring with 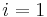$i = 1$, so the empty string, the, there, and therein are prefixes of therein. 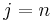A suffix is a substring with $j = n$, so the empty string, in, rein, herein, and therein are suffixes of therein.

These examples may have given the misleading impression that strings which do not represent "valid" words, such as ther, are not valid strings. This is entirely untrue; ther is also a valid prefix of therein. The definition of a string says nothing about the validity or meaning of a string. A language is a (possibly empty, often infinite) subset of 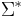$\Sigma^*$; an element of a language is often called a word (although this term should be used with caution). Thus, while every element of 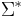$\Sigma^*$ is a valid string, not all are necessarily valid words in a language over 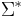$\Sigma^*$. For example, let 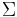$\Sigma$ be defined as the Latin alphabet and 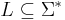$L \subseteq \Sigma^*$ be the language consisting of the representations of all valid English words. (Note that we have been careful to distinguish the words themselves from their representations as strings.) Then ther is certainly a valid string, being an element of 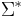$\Sigma^*$, but is not a valid word in 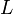$L$, since it does not represent an English word.