Shortest path
From PEGWiki
Revision as of 19:57, 15 November 2010 by Brian (Talk | contribs) (Created page with "The '''shortest paths''' problem is one of the most fundamental problems in graph theory. Given a directed graph <math>G = (V,E)</math>, possibly weighted, and a set of pairs...")
The shortest paths problem is one of the most fundamental problems in graph theory. Given a directed graph 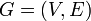 , possibly weighted, and a set of pairs of vertices
, possibly weighted, and a set of pairs of vertices 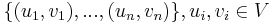 , the problem is to compute, for each
, the problem is to compute, for each  , a path in
, a path in  from
from 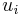 to
to 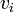 (a list of vertices
(a list of vertices 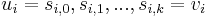 such that for all
such that for all 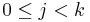 ,
, 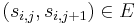 ) such that no other path in
) such that no other path in  from
from 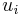 to
to 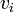 has a lower total weight.
has a lower total weight.
Shortest paths in undirected graphs can be computed by replacing each undirected edge with two arcs of the same weight, one going in each direction, to obtain a directed graph.
Contents
Variations
Three variations of the shortest path algorithm exist, and they are discussed in the following sections.
- In the single-pair shortest path problem, there is only one pair
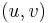 in the problem set. In other words the shortest path is desired between a single pair of vertices.
in the problem set. In other words the shortest path is desired between a single pair of vertices. - In the single-source shortest paths problem, the problem set is of the form
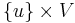 . One vertex,
. One vertex,  , is designated the source, and we wish to find the shortest paths from the source to all other vertices. (To solve the analogous single-destination shortest paths problem, we merely reverse the directions of all edges, which reduces it to single-source.)
, is designated the source, and we wish to find the shortest paths from the source to all other vertices. (To solve the analogous single-destination shortest paths problem, we merely reverse the directions of all edges, which reduces it to single-source.) - In the all-pairs shortest paths problem, the problem set is
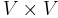 ; that is, we wish to know the shortest paths from every vertex to every other vertex.
; that is, we wish to know the shortest paths from every vertex to every other vertex.