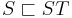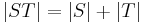String
The string is one of the most fundamental objects in computer science. Strings are intimately familiar to us in the form of text and therefore it is no wonder that the theory of strings (which is to be distinguished from the field of theoretical physics known as "string theory") is one of the most extensively studied subdisciplines of computer science.
Definitions
An alphabet, usually denoted 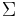 is a finite nonempty set (whose size is denoted
is a finite nonempty set (whose size is denoted 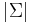 ). It is often assumed that the alphabet is totally ordered, but this is not always necessary. (Since the alphabet is finite, we can always impose a total order when it would be useful to do so, such as when constructing a dictionary.) An element of this the alphabet is known as a character.
). It is often assumed that the alphabet is totally ordered, but this is not always necessary. (Since the alphabet is finite, we can always impose a total order when it would be useful to do so, such as when constructing a dictionary.) An element of this the alphabet is known as a character.
The set of  -tuples of
-tuples of 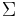 is denoted
is denoted 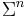 . A string of length
. A string of length  is an element of
is an element of 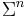 . The set
. The set 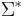 is defined
is defined 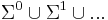 ; an element of
; an element of 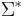 is known simply as a string over
is known simply as a string over 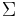 . The empty string, denoted
. The empty string, denoted 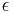 or
or 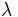 , is the unique element of
, is the unique element of 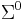 . The length of a string
. The length of a string  is denoted
is denoted 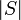 . (Note that the usual definition of "string" requires strings to have finite length, although arbitrarily long strings exist.)
. (Note that the usual definition of "string" requires strings to have finite length, although arbitrarily long strings exist.)
For ease of conceptualization, we shall usually assign a symbol, a graphical representation, to each character of the alphabet and, considering a string as a sequence of characters, render it as a sequence of symbols. We shall usually do so in boldface, but in this section we shall use italics to avoid confusion with terms being defined, hence, PEG. On other occasions we may choose to represent them with the ordered list notation, hence, [P,E,G]. (This form is useful when the symbols consist of more than one glyph, as can be the case when they are integers; see below.) We will often number the characters of strings, sometimes starting from zero, sometimes starting from one.
Examples of alphabets include:
- The binary alphabet, with exactly two characters (
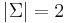 ), usually denoted 0 and 1. In virtually all computers ever built, data are strings over the binary alphabet, and are known as bit strings.
), usually denoted 0 and 1. In virtually all computers ever built, data are strings over the binary alphabet, and are known as bit strings. - The Latin alphabet, with the characters a, A, b, B, ..., z, Z (
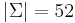 ). English words may be considered strings over the Latin alphabet.
). English words may be considered strings over the Latin alphabet. - The Unicode character set (the size of this alphabet depends somewhat on what we consider to be a valid Unicode character). Text files may be considered strings over this alphabet.
- The set of integers
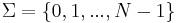 for some
for some 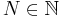 , for which
, for which  . Here the characters are also integers, and their corresponding symbols might have more than one glyph when
. Here the characters are also integers, and their corresponding symbols might have more than one glyph when 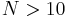 . (Recall that the definition of character is broader than the common concept of the character as the smallest, indivisible element of writing.)
. (Recall that the definition of character is broader than the common concept of the character as the smallest, indivisible element of writing.) - The set of nitrogenous bases in DNA, {A, C, G, T}, with
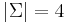 . Codons are considered members of
. Codons are considered members of 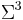 , and DNA sequences members of
, and DNA sequences members of 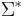 .
. - The set of universal proteinogenic amino acids, {A, C, D, E, F, G, H, I, K, L, M, N, P, Q, R, S, T, V, W, Y} (
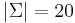 ). The primary structure of a protein is represented as a string over this alphabet. This and the preceding example are important alphabets in bioinformatics.
). The primary structure of a protein is represented as a string over this alphabet. This and the preceding example are important alphabets in bioinformatics.
A substring of a string 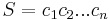 is a string with the same alphabet as
is a string with the same alphabet as  given by
given by 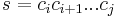 for some
for some 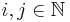 with
with 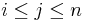 . Note that the empty string is considered a substring of all other strings. In other words, it is a series of (possibly zero) characters occurring consecutively in a string, taken in order. For example, the, in, here, and therein are all substrings of therein, as is
. Note that the empty string is considered a substring of all other strings. In other words, it is a series of (possibly zero) characters occurring consecutively in a string, taken in order. For example, the, in, here, and therein are all substrings of therein, as is 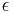 ; however, tin is not (the characters are not consecutive in the original string), nor is rine (the characters do not occur in order in the original string). A prefix is a substring with
; however, tin is not (the characters are not consecutive in the original string), nor is rine (the characters do not occur in order in the original string). A prefix is a substring with 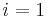 , so that
, so that 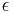 , the, there, and therein are prefixes of therein. A suffix is a substring with
, the, there, and therein are prefixes of therein. A suffix is a substring with 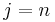 , so that
, so that 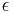 , in, rein, herein, and therein are suffixes of therein. We write
, in, rein, herein, and therein are suffixes of therein. We write 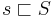 to indicate that
to indicate that  is a prefix of
is a prefix of  . Likewise the notation
. Likewise the notation  denotes that
denotes that  is a suffix of
is a suffix of  . We say that
. We say that  is a proper prefix of
is a proper prefix of  when
when 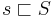 and
and 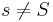 , with proper suffix defined analogously.
, with proper suffix defined analogously.
These examples may have given the misleading impression that strings which do not represent "valid" words, such as ther, are not valid strings. This is entirely untrue; ther is also a valid prefix of therein. The definition of a string says nothing about the validity or meaning of a string. A language is a (possibly empty, often infinite) subset of 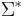 ; an element of a language is often called a word (although this term should be used with caution). Thus, while every element of
; an element of a language is often called a word (although this term should be used with caution). Thus, while every element of 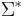 is a valid string, not all are necessarily valid words in a language over
is a valid string, not all are necessarily valid words in a language over 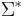 . For example, let
. For example, let 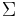 be defined as the Latin alphabet and
be defined as the Latin alphabet and 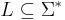 be the language consisting of the representations of all valid English words. (Note that we have been careful to distinguish the words themselves from their representations as strings.) Then ther is certainly a valid string, being an element of
be the language consisting of the representations of all valid English words. (Note that we have been careful to distinguish the words themselves from their representations as strings.) Then ther is certainly a valid string, being an element of 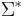 , but is not a valid word in
, but is not a valid word in 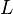 , since it does not represent an English word.
, since it does not represent an English word.
Thus, a string of length  has
has  prefixes,
prefixes,  suffixes,
suffixes,  proper prefixes,
proper prefixes,  proper suffixes, and
proper suffixes, and 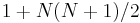 substrings. (Here we consider two substrings to be distinct if they start or end at different indices, except that the empty string is counted only once; see also counting distinct substrings.)
substrings. (Here we consider two substrings to be distinct if they start or end at different indices, except that the empty string is counted only once; see also counting distinct substrings.)
Two strings with the same alphabet can be concatenated. To concatenate two strings is to link them together to give a new string which begins with the first and ends with the second with no overlap. Formally, the concatenation of strings  and
and  is denoted
is denoted 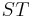 and has the following three properties:
and has the following three properties:
For example, concatenating there and in gives therein. So do concatenating the and rein, or 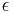 and therein, or therein and
and therein, or therein and 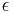 . Note that in general, concatenation is not commutative.
. Note that in general, concatenation is not commutative.