Topological sort
The topological sorting problem is the problem of determining a topological ordering of a digraph's vertices, that is, a list of the vertices such that an edge never exists from a vertex later in the list to a vertex earlier in the list.
Motivation
Topological sorting is perhaps best understood as the problem of dependency resolution. Examples are given here:
- To earn a degree, a student has to complete certain required courses. However, these cannot be taken in just any order; some of these courses are prerequisites for others. For example, the Introduction to Algorithms in Bioinformatics course may depend on the Introduction to Algorithms course, which may depend on the Introduction to Data Structures course, which may in turn depend on the Introduction to Programming course. This is a dependency relationship; taking later courses depends on taking prerequisite earlier courses. We can construct a graph in which each vertex is a course and a directed edge exists from
 to
to  if and only if the course corresponding to
if and only if the course corresponding to  is a prerequisite for the course corresponding to
is a prerequisite for the course corresponding to  . Topologically sorting this graph will give a possible order in which the courses may be taken (although it cannot, of course, be used to solve the more serious problem of scheduling conflicts).
. Topologically sorting this graph will give a possible order in which the courses may be taken (although it cannot, of course, be used to solve the more serious problem of scheduling conflicts). - Large software applications are usually heavily modularized, where, generally, each module is a chunk of code of manageable size containing a simple group of related functions stored in a single file or a small number of files. These modules may depend on simpler modules, which may in turn depend on simpler modules, and so on down. For example, the compiler
gccmay depend on the arithmetic librarygmp, which may depend on the macro languagem4, which may depend on the C standard librarylibc. We cannot compile a module until all its dependencies have already been compiled. If each module is a vertex and an edge exists from one vertex to another if and only if the latter's module depends on the former's, then topologically sorting this graph gives a valid order in which we may compile all the modules. (The program/usr/bin/tsortwas provided on many UNIX-based systems exactly for this purpose; it has been superseded bymake, but it still exists on some modern systems.) - In some video games, each level consists of exploring a particular part of the world map. There is no preset order on how to explore the map, but some areas may not be explored right away because they depend on "earlier" areas having been explored (and presumably "beaten"). We let each area of the map be a vertex and let there be an edge from one vertex to another if the former's area must be explored before the latter's. A topological ordering of this graph corresponds to a valid order in which the map may be explored.
Existence of a solution
We first note that being a DAG is necessary for a digraph to have a topological ordering. This is not hard to see; if the graph contains a cycle,  , then
, then 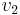 must occur after
must occur after 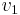 in the topological ordering,
in the topological ordering, 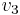 must occur after
must occur after 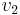 , and so on, but then
, and so on, but then 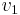 must occur after
must occur after 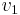 , leading to the absurd conclusion that
, leading to the absurd conclusion that 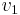 must occur after itself in the list. Intuitively, if a cyclic dependency exists among a set of tasks, none of those tasks can ever be executed.
must occur after itself in the list. Intuitively, if a cyclic dependency exists among a set of tasks, none of those tasks can ever be executed.
The next question is whether this condition is also sufficient. That is, is it true that a digraph may be topologically ordered if and only if it is a DAG? The answer is yes.
Theorem: Every DAG may be topologically ordered.
Proof: By induction on the number of vertices. Clearly, a DAG with one vertex may be topologically ordered; the list in this case consists only of the vertex itself. Now, suppose that any DAG with 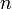 vertices may be ordered, and now consider any DAG with
vertices may be ordered, and now consider any DAG with 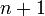 vertices. Recall that every DAG has at least one source. We let this be the first entry in our list. The subgraph left behind, which has
vertices. Recall that every DAG has at least one source. We let this be the first entry in our list. The subgraph left behind, which has 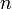 vertices, is still acyclic; obviously cycles cannot be introduced by removing edges. By the inductive hypothesis, we can topologically order this subgraph. Then, we append the topological ordering of this subgraph to the end of our current list, to obtain a list of vertices of the original
vertices, is still acyclic; obviously cycles cannot be introduced by removing edges. By the inductive hypothesis, we can topologically order this subgraph. Then, we append the topological ordering of this subgraph to the end of our current list, to obtain a list of vertices of the original 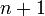 -vertex graph with the source in the first position. Now, given any two vertices
-vertex graph with the source in the first position. Now, given any two vertices  and
and  on the list, where, without loss of generality,
on the list, where, without loss of generality,  precedes
precedes  , either
, either  is the first entry (the source), in which case there is obviously no
is the first entry (the source), in which case there is obviously no  -
- edge, or
edge, or  and
and  are both not the first entry, in which case they must be properly ordered as they belong to the topologically ordered tail of the list. Therefore this new list of
are both not the first entry, in which case they must be properly ordered as they belong to the topologically ordered tail of the list. Therefore this new list of 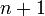 vertices is a topological ordering of the
vertices is a topological ordering of the 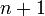 -vertex graph.
-vertex graph. 
Uniqueness
In general, the topological ordering is not unique; there may be several different orders in which the graph may be traversed that satisfy the topological ordering property. It is, however, unique if and only if the partial order represented by the DAG is in fact a total order; that is, when the DAG has a Hamiltonian path, or, equivalently, the transitive closure of the DAG is the complete graph.