Big numbers

Big numbers, known colloquially as bignums (adjectival form bignum, as in bignum arithmetic) are integers whose range exceeds those of machine registers. For example, most modern processors possess 64-bit registers which can be used to store integers up to 2⁶⁴-1. It is usually possible to add, subtract, multiply, or divide such integers in a single machine instruction. However, such machines possess no native implementation of arithmetic on numbers larger than this, nor any native means of representing them. In some applications, it might be necessary to work with numbers with hundreds or even thousands of digits.

Of course, humans have no problems with working with numbers greater than 2⁶⁴-1, other than the fact that it's tedious; we just write them out and use the same algorithms we use on smaller numbers: add column-by-column and carry, and so on. This turns out to be the key to working with bignums in computer programs too.

Fixed versus dynamic bignums

There are, in principle, two kinds of bignum implementation. Suppose we know in advance the maximum size of the integers we might be working with. For example, in TREE1@SPOJ, we are asked to report the number of permutations which satisfy a certain property. There are only up to 30 elements, so we know that the answer will not exceed 30! = 265252859812191058636308480000000, which has 33 digits. It is not terribly difficult to implement the solution in such a way that no intermediate variable is ever larger than this. So we could, for example, use a string of length 33 to store all integers used in the computation of the answer (where numbers with fewer than 33 digits are padded with zeroes on the left), and treat all numbers as though they had 33 digits. This is probably the easiest type of bignum to implement.

On the other hand, sometimes it is not so easy to determine in advance the size of the numbers we might be working with, or a problem might have bundled test cases and a strict time limit, forcing the programmer to make the small cases run more quickly than the large ones. When this occurs it is a better idea to use dynamic bignums, which can expand or shrink according to their length. Dynamic bignums are trickier to code than fixed ones. Because extensible array data structures such as C++'s std::vector often support efficient insertion at the back but unacceptable linear-time performance on insertion at the front, it is advisable to store dynamic bignums in little-endian format or backward (see next section)

Representation

Bignums are represented using a radix system. This means that a bignum is stored in a base 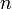$n$ representation, where the choice of 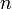$n$ is based on the application. Precisely, the number 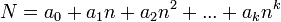$N = a_0 + a_1 n + a_2 n^2 + ... + a_k n^k$ is stored by giving the values 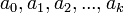$a_0, a_1, a_2, ..., a_k$. Here are a few common possibilities:

• If we let the radix be 10:

• ASCII representation: the number is represented by a string which literally contains the number's digits as characters: {'2','6',
• BCD representation: an array of digits.

• If we let the radix be 10⁹, we can store nine digits in each array entry. For example, 30! would be stored as either {265252,859812191,058636308,480000000} or {480000000,058636308,859812191,265252}, depending on whether we choose to store the numbers forward or backward. Note that, in either case, we must take care to group digits starting from the decimal point and moving left, instead of starting at the most significant digit and moving right, to avoid complicating the code and eroding performance considerably.
• If we let the radix be 2³², we use a sequence of 32-bit unsigned integer typed variables to store the bignum. Here, we could store it as either {00000D13₁₆,F6370F96₁₆,865DF5DD₁₆,54000000₁₆} (big-endian) or {54000000₁₆,865DF5DD₁₆,F6370F96₁₆,00000D13₁₆} (little-endian).