Difference between revisions of "String"

Revision as of 07:05, 16 November 2010

The string is one of the most fundamental objects in computer science. Strings are intimately familiar to us in the form of text and therefore it is no wonder that the theory of strings (which is to be distinguished from the field of theoretical physics known as "string theory") is one of the most extensively studied subdisciplines of computer science.

Definitions

An alphabet, usually denoted 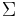$\Sigma$ is a finite nonempty set (whose size is denoted 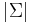$|\Sigma|$ ). It is often assumed that the alphabet is totally ordered, but this is not always necesary. An element of this the alphabet is known as a character.

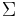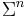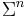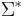The set of $n$ -tuples of $\Sigma$ is denoted $\Sigma^n$ . A string of length $n$ is an element of $\Sigma^n$ . The set $\Sigma^*$ is defined 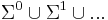$\Sigma^0 \cup \Sigma^1 \cup ...$ ; an element of 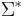$\Sigma^*$ is known simply as a string over 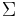$\Sigma$ . The empty string, denoted 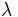$\lambda$ , is the unique element of 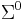$\Sigma^0$ . Strings must have finite length, but there is no limit on the length of a string.

Examples of alphabets include:

The binary alphabet, 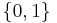$\{0, 1\}$ . There are two characters, usually denoted 0 and 1. In virtually all computers ever built, data are strings over the binary alphabet, and are known as bit strings.
The Latin alphabet, consisting of the characters a, A, b, B, ..., z, Z. English words may be considered strings over the Latin alphabet.
The Unicode character set. Text files may be considered strings over this alphabet.
The set of integers 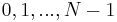$0, 1, ..., N-1$ for some 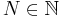$N \in \mathbb{N}$ . Here the characters are actually integers. (Recall that the definition of character is broader than the common concept of the character as the smallest, indivisible element of writing.)

Difference between revisions of "String"

Revision as of 07:05, 16 November 2010

Definitions

Navigation menu

Personal tools

Namespaces

Variants

Views

More

Search

Navigation

Tools