Difference between revisions of "Heavy-light decomposition"

Revision as of 01:39, 8 January 2010

The heavy-light (H-L) decomposition of a rooted tree is a method of partitioning of the vertices of the tree into disjoint paths (all vertices have degree two, except the endpoints of a path, with degree one) that gives important asymptotic time bounds for certain problems involving trees.

Definition

The heavy-light decomposition of a tree 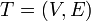$T=(V,E)$ is a coloring of the tree's edges. Each edge is either heavy or light. To determine which, consider the edge's two endpoints: one is closer to the root, and one is further away. If the size of the subtree rooted at the latter is more than half that of the subtree rooted at the latter, the edge is heavy. Otherwise, it is light.

Properties

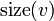Denote the size of a subtree rooted at vertex $v$ as $\operatorname{size}(v)$ .

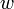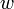Suppose that a vertex $v$ has two children $u$ and $w$ and the edges $v$ - $u$ and $v$ - $w$ are both heavy. Then, 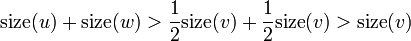$\operatorname{size}(u) + \operatorname{size}(w) > \frac{1}{2}\operatorname{size}(v)+\frac{1}{2}\operatorname{size}(v) > \operatorname{size}(v)$ . This is a contradiction, since we know that 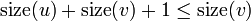$\operatorname{size}(u) + \operatorname{size}(v) + 1 \le \operatorname{size}(v)$ . ( $v$ , of course, may have more than two children.) We conclude that there may be at most one heavy edge of all the edges joining any given vertex to its children.

At most two edges incident upon a given vertex may then be heavy: the one joining it to its parent, and at most one joining it to a child. Consider the subgraph of the tree in which all light edges are removed. Then, all resulting connected components are paths (although some contain only one vertex and no edges at all) and two neighboring vertices' heights differ by one. We conclude that the heavy edges, along with the vertices upon which they are incident, partition the tree into disjoint paths, each of which is part of some path from the root to a leaf.

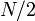Suppose a tree contains $N$ vertices. If we follow a light edge from the root, the subtree rooted at the resulting vertex has size at most $N/2$ ; if we repeat this, we reach a vertex with subtree size at most 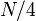$N/4$ , and so on. It follows that the number of light edges on any path from root to leaf is at most $\lg N$ .

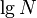Applications

The utility of the H-L decomposition lies in that problems involving paths between nodes can often be solved more efficiently by "skipping over" heavy paths rather than considering each edge in the path individually. For example consider the following problem: A weighted, rooted tree is given followed by a large number of queries and modifications interspersed with each other. A query asks for the distance between a given pair of nodes and a modification changes the weight of a specified edge to a new (specified) value. How can the queries and modifications be performed efficiently?

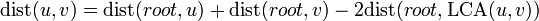First of all, we notice that the distance between nodes $u$ and $v$ is given by $\operatorname{dist}(u,v) = \operatorname{dist}(root,u) + \operatorname{dist}(root,v) - 2\operatorname{dist}(root,\operatorname{LCA}(u,v))$ . Hence, if we can efficiently solve lowest common ancestor queries (which is easy if we preprocess the tree), as well as queries of a node's distance from the root, a solution to this problem follows trivially.

To solve this simpler problem of querying the distance from the root to a given node (and modifying edge weights efficiently), we can use the H-L decomposition. We start at the given node and "walk up" the tree until we reach the root. When we encounter a light edge, we merely traverse it, adding its weight to the running total. (The total time spent on such operations is 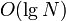$O(\lg N)$ , because there are 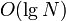$O(\lg N)$ light edges on the path.) When we encounter a heavy edge, we "skip" all the subsequent heavy edges, adding all of their weights to our running total and arriving at a vertex which is joined to its parent by a light edge (or at the root).

To perform this "skipping" operation, every vertex which is joined to its parent by a heavy edge must be augmented with a pointer to the vertex at the top of the heavy path, so that we can immediately find the next vertex up, skipping over all the black edges along the way. To find the sum of the weights of all of the skipped edges, we make a query on a structure such as a segment tree or a binary indexed tree. (The elements of the underlying array of the segment tree or BIT are the weights of the edges on the heavy path, in order of course; the query is then simply "find the sum of all elements between the first and the given", which can be answered in 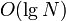$O(\lg N)$ time.)

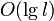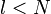Thus, when we perform a modification, we modify either a light edge, which requires only changing the variable storing its weight, or a heavy edge, which requires us to change one element in the data structure used along the heavy paths, which is doable in $O(\lg l)$ time, where $l$ is the length of the path. Since $l<N$ , we conclude that modifications can be performed in time logarithmic in the size of the tree.

In a query, we consider at most logarithmically many light edges, so that the total time spent considering light edges is 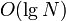$O(\lg N)$ . Heavy paths are more complicated to analyze; clearly, the number of heavy paths encountered is at most one more than the number of light edges, so that there are at most 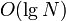$O(\lg N)$ of them, and the time spent on each is logarithmic in its size, so that an upper bound of 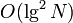$O(\lg^2 N)$ trivially follows. It turns out that a stronger bound holds; the time taken for an update is also, in fact, $O(\lg N)$ .

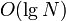References

Wang, Hanson. (2009). Personal communication.

Difference between revisions of "Heavy-light decomposition"

Revision as of 01:39, 8 January 2010

Contents

Definition

Properties

Applications

References

Navigation menu

Personal tools

Namespaces

Variants

Views

More

Search

Navigation

Tools