Difference between revisions of "Longest common substring"

Revision as of 22:11, 18 March 2011

Not to be confused with Longest common subsequence.

The longest common substring problem is the problem of finding a string of maximum length which is simultaneously a substring of two or more given strings (usually two). For example, the longest common substring of atlas and elastic is las. This problem is much less applicable (in real life) than the more error-tolerant longest common subsequence problem, but it is theoretically interesting.

Discussion

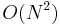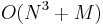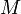We can observe immediately that this problem is solvable in polynomial time, because a string of length $N$ has $O(N^2)$ substrings, allowing us to simply list all substrings of each string and then find the longest entry(ies) common to both strings. This, however, gives $O(N^3+M)$ time (assuming we have two strings of lengths $N$ and $M$ and we use an efficient string search algorithm). In addressing the question of whether it is possible to do better, we at first consider three variations on the problem:

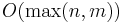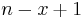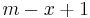Return all longest common substrings. There may only be $O(\max(n,m))$ of these, where $n$ is the length of the first string and $n$ is the length of the second. This is because there are only $n-x+1$ substrings of any given length $x$ in the first string, and $m-x+1$ in the second string.
Return any longest common substring.
Return only the length of a longest common substring.