Difference between revisions of "Disjoint sets"
(Created page with "The '''disjoint sets''' problem is that of efficiently maintaining a collection <math>\mathcal{C}</math> of disjoint subsets of some universe <math>U</math>. Specifically, we ass...") |
(No difference)
|
Revision as of 21:35, 4 March 2011
The disjoint sets problem is that of efficiently maintaining a collection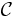 
of disjoint subsets of some universe 
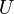. Specifically, we assume that initially 
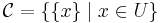, that is, each element of the universe is contained in a singleton. Then, we wish to efficiently support two operations:
- Find the set that contains a given element
. By this we mean that we imagine we have assigned some unique identifier to each set in our collection, so that if we execute two find operations in succession on two elements that are located in the same set, then the same value is returned, whereas different values are returned if they are in different sets. - Unite two given sets
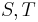in the collection, that is, remove 
and 
from 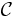, and add 
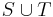to .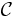
For this reason, the disjoint sets problem is often called the union-find problem.
A configuration of disjoint sets is a model of an equivalence relation, with each set an equivalence class; two elements are equivalent if they are in the same set. Often, when discussing an equivalence relation, we will choose one element in each equivalence class to be the representative of that class (and we say that such an element is in canonical form). Then the find operation can be understood as determining the representative of the set in which the query element is located. When we unite two sets, we either use the representative of one of the two sets as the representative of the new, united set, or we pick a new element altogether to be the representative.
