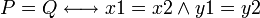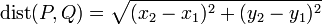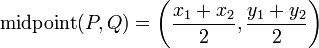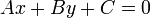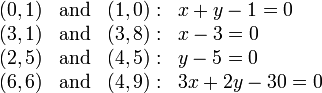Difference between revisions of "Computational geometry"
(Created page with '=Introduction and Scope= ==Definition== '''Computational geometry''', as one can easily guess from the name, is the branch of computer science encompassing geometrical problems a…') |
(No difference)
|
Revision as of 01:01, 6 November 2009
Contents
Introduction and Scope
Definition
Computational geometry, as one can easily guess from the name, is the branch of computer science encompassing geometrical problems and how their solutions may be implemented (efficiently, one would hope) on a computer.
Scope
Essentially all of the computational geometry you will encounter in high-school level competitions, even
competitions such as the IOI, is plane Euclidean geometry, the noble subject on which Euclid wrote his
Elements and a favorite of mathematical competitions. You would be hard-pressed to find contests containing geometry problems in three dimensions or higher. You also do not need to worry about non-Euclidean
geometries in which the angles of a triangle don't quite add to 180 degrees, and that sort of thing. In short,
the type of geometry that shows up in computer science contests is the type of geometry to which you have
been exposed, countless times, in mathematics class, perhaps without being told that other geometries exist.
So in all that follows, the universe is two-dimensional, parallel lines never meet, the area of a circle with
radius  is
is 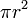 , and so on.
, and so on.
Points
Introduction
Many would claim that the point is the fundamental unit of geometry. Lines, circles, and polygons are all merely (infinite) collections of points and in fact we will initially consider them as such in order to derive several important results. A point is an exact location in space. Operations on points are very easy to perform computationally, simply because points themselves are such simple objects.
Representation: Cartesian coordinates
In our case, "space" is actually a plane, two-dimensional. That means that we need two real numbers to
describe any point in our space. Most of the time, we will be using the Cartesian (rectangular) coordinate
system. In fact, when points are given in the input of a programming problem, they are almost always
given in Cartesian coordinates. The Cartesian coordinate system is easy to understand and every pair of
real numbers corresponds to exactly one point in the plane (and vice versa), making it an ideal choice for
computational geometry.
Thus, a point will be represented in the computer's memory by an ordered pair of real numbers. Due to the
nature of geometry, it is usually inappropriate to use integers, as points generally do not fit neatly into the
integer lattice! Even if the input consists only of points with integer coordinates, calculations with these
coordinates will often yield points with non-integral coordinates, which can often cause counter-intuitive
behavior that will have you scratching your head! For example, in C++, when one integer is divided by
another, the result is always truncated to fit into an integer, and this is usually not desirable.
Determining whether two points coincide
Using the useful property of the Cartesian coordinate system discussed above, we can determine whether
or not two given points coincide. Denote the two points by  and
and  , with coordinates
, with coordinates 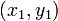 and
and 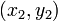 , respectively, and then:
, respectively, and then:
Read: The statement that  and
and  are the same point is equivalent to the statement that their corresponding coordinates are equal. That is,
are the same point is equivalent to the statement that their corresponding coordinates are equal. That is,  and
and  having both the same x-coordinates and also the same y-coordinates is both sufficient and necessary for the two to be the same point.
having both the same x-coordinates and also the same y-coordinates is both sufficient and necessary for the two to be the same point.
The distance between two points
To find the distance between two points, we use the Euclidean formula. Given two points 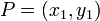 and
and 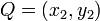 , the distance between them is given by:
, the distance between them is given by:
(Note that when we write 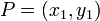 , we mean that
, we mean that  is a point with x-coordinate
is a point with x-coordinate 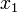 and y-coordinate
and y-coordinate 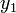 .)
.)
The midpoint of the line segment joining two points
Given two points, how may we find the midpoint of the line segment joining two points? (Intuitively, it is the point that is "right in the middle" of two given points. One might think that we require some knowledge about line segments in order to answer this, but it is for precisely the reason that, in a certain sense, no such knowledge is required to understand the answer, that this operation is found in the Points section. So, given two points 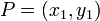 and
and 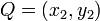 , this midpoint is given by
, this midpoint is given by
Lines
What is a line?
In axiomatic geometry, some terms such as point and line are left undefined, because an infinite regression of definitions is clearly absurd. In the algebraic approach we are taking, the line is defined in terms of the points which lie on it; that will be discussed in the following section. It will just be pointed out here that the word line is being used in the modern mathematical sense. Lines are straight; the terms line and straight line shall have identical meaning. Lines extend indefinitely in both directions, unlike rays and line segments.
The equation of a line
In computational geometry, we have to treat all aspects of geometry algebraically. Computers are excellent at dealing with numbers but have no mechanism for dealing with geometrical constructions; rather we must reduce
them to algebra if we wish to accomplish anything.
In Ontario high schools, the equation of a line is taught in the ninth grade. For example, the line which passes through the points (0,1) and (1,0) has the equation 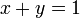 . Precisely, this means that for a given point
. Precisely, this means that for a given point 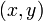 , the statement
, the statement 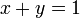 is equivalent to, or sufficient and necessary for, the point to be on the line.
is equivalent to, or sufficient and necessary for, the point to be on the line.
The form of the equation of the line which is first introduced is generally the 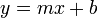 , in which
, in which 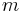 is the slope of the line and
is the slope of the line and 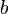 is the y-intercept. For example, the line discussed above has the equation
is the y-intercept. For example, the line discussed above has the equation 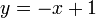 , that is,
, that is, 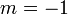 and
and 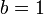 . By substituting different values for
. By substituting different values for 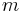 and
and 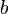 , we can obtain various (different) lines. But there's a problem here: if your line is vertical, then it is not
possible to choose values of
, we can obtain various (different) lines. But there's a problem here: if your line is vertical, then it is not
possible to choose values of 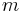 and
and 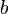 for the line. (Try it!) This is because the y-coordinate is no longer a function of the x-coordinate.
for the line. (Try it!) This is because the y-coordinate is no longer a function of the x-coordinate.
Thus, when dealing with lines computationally, it seems we would need to have
a special case: check if the line is vertical; if so, then do something,
otherwise do something else. This is a time-consuming and error-prone way of
coding.
Standard Form of the equation of a line
Even though the slope-intercept form cannot describe a vertical line, there is an equation that describes a vertical line. For example, the line passing through (3,1) and (3,8) is 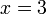 . In fact, almost any line can be described by an equation of the form
. In fact, almost any line can be described by an equation of the form 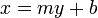 . (Try it if you don't believe me. I have merely switched around
. (Try it if you don't believe me. I have merely switched around  and
and 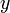 from the slope-intercept form.) Except... horizontal lines. So we have two forms of the equation of a line: one which fails on vertical lines and one which fails on horizontal lines. Can we combine them to give an equation of the line which is valid for any
line?
from the slope-intercept form.) Except... horizontal lines. So we have two forms of the equation of a line: one which fails on vertical lines and one which fails on horizontal lines. Can we combine them to give an equation of the line which is valid for any
line?
As it turns out, it is indeed possible.
That equation, the standard form of the equation of the line is:
By substituting appropriate values of  ,
,  , and
, and 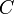 , one can
describe any line with this equation. And by storing values of
, one can
describe any line with this equation. And by storing values of  ,
,  , and
, and 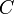 , one can represent a line in the computer's memory.
Here are some pairs of points and possible equations for each:
, one can represent a line in the computer's memory.
Here are some pairs of points and possible equations for each:
As you can see, it handles vertical and horizontal lines properly, as well
as lines which are neither.
Note that the standard form is not unique: for example, the equation of the
first line could have just as well been 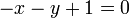 or perhaps
or perhaps
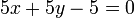 . Any given line has infinitely many representations
in the standard form. However, each standard form representation describes
at most one line.
. Any given line has infinitely many representations
in the standard form. However, each standard form representation describes
at most one line.
If  and
and  are both zero, the standard form describes no line
at all.
are both zero, the standard form describes no line
at all.