Difference between revisions of "PEGWiki:Notational conventions"
(→Technical notation) |
m (→Both text-mode and math-mode) |
||
| (6 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | This page documents some conventions to be followed when writing | + | This page documents some conventions to be followed when writing articles on PEGWiki. These are not binding policy on PEGWiki, but following them should minimize confusion and promote consistency across articles. You won't get in trouble for not following them, but what you write is likely to be slightly modified to conform with these conventions if it doesn't initially. If you see arcane or unfamiliar notation anywhere in an article, but especially in a pseudocode block, you may find its meaning here. Changes to these conventions should be discussed on the [[PEGWiki_talk:Notational conventions|talk page]]. |
| − | = | + | ==Pseudocode conventions== |
| + | ===Both text-mode and math-mode=== | ||
* '''Structure should be indicated by indentation''', as in Python. Adding braces <code>{}</code> as in C or words such as <code>begin</code> and <code>end</code> as in Pascal would introduce unnecessary clutter into pseudocode blocks. '''Do not use tabs''' for indentation. Five spaces is a good guideline. (In LaTeX pseudocode, this means five full-width spaces (a full-width space is "<code>\ </code>").) | * '''Structure should be indicated by indentation''', as in Python. Adding braces <code>{}</code> as in C or words such as <code>begin</code> and <code>end</code> as in Pascal would introduce unnecessary clutter into pseudocode blocks. '''Do not use tabs''' for indentation. Five spaces is a good guideline. (In LaTeX pseudocode, this means five full-width spaces (a full-width space is "<code>\ </code>").) | ||
| − | * The <code>for</code>, <code>if</code>/<code>else</code>, and <code>while</code> statements should not be followed by words like "do" or "then"; pseudocode is intended for humans, not machines. | + | * The <code>for</code>, <code>if</code>/<code>else</code>, and <code>while</code> statements should not be followed by words like "do" or "then", as in Pascal, but should stand alone, as in C; pseudocode is intended for humans, not machines. |
* Similarly, statements should not end in semicolons. | * Similarly, statements should not end in semicolons. | ||
* Indices into arrays should be placed in square brackets, <code>[]</code>. The Pascal convention of separating indices by commas is preferred to the C convention of having a separate set of brackets for each index (simply by virtue of being nicer and more intuitive), but the latter may be occasionally appropriate to reinforce the interpretation of the array's structure. Use your common sense. | * Indices into arrays should be placed in square brackets, <code>[]</code>. The Pascal convention of separating indices by commas is preferred to the C convention of having a separate set of brackets for each index (simply by virtue of being nicer and more intuitive), but the latter may be occasionally appropriate to reinforce the interpretation of the array's structure. Use your common sense. | ||
* Parameter lists should be enclosed in parentheses, <code>()</code>, and parameters should be separated by commas. | * Parameter lists should be enclosed in parentheses, <code>()</code>, and parameters should be separated by commas. | ||
| − | * A function header should contain with the word <code>function</code>, the function's name, and the function's parameter list, in that order. The body of a function should be indented. | + | * A function header should contain with the word <code>function</code>, the function's name, and the function's parameter list, in that order, as in PHP or JavaScript. The body of a function should be indented. |
* If something is not a real command, ''e.g.'' <code>input</code> or <code>print</code>, it should not be written like a function (its parameter list should not have parentheses). | * If something is not a real command, ''e.g.'' <code>input</code> or <code>print</code>, it should not be written like a function (its parameter list should not have parentheses). | ||
* Object-oriented code should be used wherever appropriate, and '''nowhere else'''. The members of an object should be indicated by the dot operator <code>.</code>. For example, it makes sense to represent a data structure as an object (which encapsulates the structure's data). However, please do not wrap an entire algorithm in an object as would be done in Java; that is pointless and only leads to clutter. | * Object-oriented code should be used wherever appropriate, and '''nowhere else'''. The members of an object should be indicated by the dot operator <code>.</code>. For example, it makes sense to represent a data structure as an object (which encapsulates the structure's data). However, please do not wrap an entire algorithm in an object as would be done in Java; that is pointless and only leads to clutter. | ||
| − | * The mod operator should never return a negative result; the number-theoretic convention of always yielding a non-negative integer should be followed. | + | * The mod operator should never return a negative result; the number-theoretic convention of always yielding a non-negative integer should be followed, as in Scheme. |
| − | =Text-mode | + | ===Text-mode only=== |
* Variable assignment should occur through the use of a single equals sign, <code>=</code>, although the Pascal notation of <code>:=</code> is also acceptable. | * Variable assignment should occur through the use of a single equals sign, <code>=</code>, although the Pascal notation of <code>:=</code> is also acceptable. | ||
* Equality testing should also occur through the use of a single equals sign, <code>=</code>, but is distinguished from variable assignment by context. For example, if it is preceded by <code>if</code>, it is an equality test, and if it stands alone, it is an assignment. The C notation of <code>==</code> should be avoided. | * Equality testing should also occur through the use of a single equals sign, <code>=</code>, but is distinguished from variable assignment by context. For example, if it is preceded by <code>if</code>, it is an equality test, and if it stands alone, it is an assignment. The C notation of <code>==</code> should be avoided. | ||
| − | * The symbols <code><=</code> | + | * The symbols <code><=</code>, <code>>=</code>, and <code><></code> are equally acceptable as their single-symbol Unicode counterparts <code>≤</code>, <code>≥</code>, and <code>≠</code>, but in most other cases a Unicode symbol should be used whenever both necessary and possible. For example, <code>oo</code> for <code>∞</code> is unacceptable. |
* Variables (and named constants) from pseudocode blocks which are referenced in the article text should be in <i>italics</i>; all other items, such as functions and literal constants, should be <code>monospaced</code>. The exception is literal numerical constants; it is acceptable not to format them specially, since they cause no confusion. | * Variables (and named constants) from pseudocode blocks which are referenced in the article text should be in <i>italics</i>; all other items, such as functions and literal constants, should be <code>monospaced</code>. The exception is literal numerical constants; it is acceptable not to format them specially, since they cause no confusion. | ||
| − | =Math-mode | + | ===Math-mode only=== |
* The LaTeX <code>\sqrt</code> command is almost always preferable to typing out <math>\operatorname{sqrt}</math>. | * The LaTeX <code>\sqrt</code> command is almost always preferable to typing out <math>\operatorname{sqrt}</math>. | ||
* The vinculum (horizontal bar) to indicate division (produced by the <code>\frac</code> command) is usually best, but if the numerator or denominator is complex, a single slash <math>/</math> is preferable when it improves readability or overall aesthetic appeal. | * The vinculum (horizontal bar) to indicate division (produced by the <code>\frac</code> command) is usually best, but if the numerator or denominator is complex, a single slash <math>/</math> is preferable when it improves readability or overall aesthetic appeal. | ||
| Line 26: | Line 27: | ||
* Variable assignment should occur through the <math>\gets</math> symbol (LaTeX code: <code>\gets</code>) | * Variable assignment should occur through the <math>\gets</math> symbol (LaTeX code: <code>\gets</code>) | ||
| − | =Technical notation= | + | ==Technical notation== |
| − | ==Sets and related items== | + | ===Sets and related items=== |
| − | * | + | * Items enclosed in braces <math>\{\}</math> and separated by commas form a set or multiset. For example, <math>\{1,2,3\}</math> is a set containing the elements 1, 2, and 3. Normally they form a set; they form a multiset if stated otherwise. The difference is that a set contains no duplicate elements. Sets and multisets should be ''typed'': that is, a set or multiset should not contain elements of different types. However, a set/multiset may itself contain sets/multisets, or any other kind of item. |
| − | + | * A set/multiset that contains no elements is denoted ∅ (LaTeX: <math>\emptyset</math>). | |
| − | * Items enclosed in parentheses () and separated by commas form a ''tuple''. For example, <math>(A,B)</math> is an ordered pair (a tuple with two elements). Tuples may contain elements of different types. | + | * A set/multiset that contains all elements of a given type is denoted <math>U</math>, the universal set. The type can generally be inferred from context. |
| − | ==Graph theory== | + | * Items enclosed in parentheses <math>()</math> and separated by commas form a ''tuple''. For example, <math>(A,B)</math> is an ordered pair (a tuple with two elements). Tuples, unlike sets and multisets, may contain elements of different types, and, again unlike sets and multisets, they have a fixed size. |
| + | * Equality of tuples is denoted by an equals sign, <math>=</math>. Two tuples are equal if and only if they are equal in size and all corresponding pairs of elements are equal; hence, <math>(B,A) \neq (A,B) \neq (A,B,C)</math>. | ||
| + | * The symbol ∈ means "is a member of", and ∉ means "is not a member of ". | ||
| + | * The union of two sets or multisets <math>S</math> and <math>T</math> is denoted <math>S\cup T</math>, their intersection <math>S\cap T</math>, and their difference <math>S\setminus T</math>. | ||
| + | * The size or cardinality of a set or multiset <math>S</math> is denoted <math>|S|</math>. | ||
| + | * The symbols <math>\subseteq</math>, <math>\subsetneq</math>, <math>\supseteq</math>, and <math>\supsetneq</math> denote subset, proper subset, superset, and proper superset, respectively. The symbols <math>\subset</math> and <math>\supset</math> are ambiguous and should be avoided. These relations are defined on multisets similarly to how they are defined on sets. | ||
| + | * The Cartesian product of two sets or multisets <math>S</math> and <math>T</math> is denoted <math>S \times T</math>. | ||
| + | * The complement of a set is denoted <math>S'</math>; the complement is not defined on multisets. | ||
| + | * The sum of two multisets <math>S</math> and <math>T</math> is denoted <math>S \uplus T</math>; this is not defined on ordinary sets. | ||
| + | * A ''list'' is written like a set but with square brackets, <math>[\,]</math>. It is an ordered collection of elements of the same type. A list is like a set in that its size is not fixed but elements can be added and removed. It is like a tuple in that two lists are considered equal if and only if they are of the same size and all pairs of corresponding elements are equal. Hence, <math>[1,2,3] \neq [1,3,2]</math>, as their elements are in different orders. | ||
| + | * Two lists written with a plus sign between them represents the concatenation of the two lists: hence, <math>[1,2] + [3,4] = [1,2,3,4]</math>. Notice that concatenation is noncommutative. | ||
| + | * <math>\mathbb{N}_1</math> represents the positive integers. <math>\mathbb{N}_0</math> represents the non-negative integers. Unless the intended meaning is absolutely clear from context, please use a subscript 0 or 1 instead of simply writing <math>\mathbb{N}</math>. | ||
| + | |||
| + | ===Graph theory=== | ||
* Vertices in graphs should be given either non-negative integers or letters as labels; letters however must be italicized except when in code blocks. Subscripts on letters are okay: we might for example label the vertices of a bipartite graph as <math>A_1,A_2,A_3,A_4,\ldots,B_1,B_2,B_3,B_4,\ldots</math>, in which edges exist only between <math>A</math>s and <math>B</math>s. Subscripts on numbers, however, are not. | * Vertices in graphs should be given either non-negative integers or letters as labels; letters however must be italicized except when in code blocks. Subscripts on letters are okay: we might for example label the vertices of a bipartite graph as <math>A_1,A_2,A_3,A_4,\ldots,B_1,B_2,B_3,B_4,\ldots</math>, in which edges exist only between <math>A</math>s and <math>B</math>s. Subscripts on numbers, however, are not. | ||
* An edge in a directed graph is an ordered pair of vertices. For example, if a graph has an edge from <math>A</math> to <math>B</math>, then this can be described as <math>(A,B)</math>. An edge in an undirected graph is an unordered pair, or a set containing two vertices: for example, <math>\{A,B\}</math>. (If self-loops are allowed, then it's actually a multiset.) | * An edge in a directed graph is an ordered pair of vertices. For example, if a graph has an edge from <math>A</math> to <math>B</math>, then this can be described as <math>(A,B)</math>. An edge in an undirected graph is an unordered pair, or a set containing two vertices: for example, <math>\{A,B\}</math>. (If self-loops are allowed, then it's actually a multiset.) | ||
* A graph is an ordered pair of two sets: <math>V</math> and <math>E</math>. The former is the set of vertices, and the latter the set of edges. We can write <math>G = (V,E)</math> to indicate that the graph <math>G</math> has vertex set <math>V</math> and edge set <math>E</math>. Also, given some graph <math>G</math>, <math>V(G)</math> is the vertex set of <math>G</math>, and <math>E(G)</math> is the edge set of <math>G</math>. An example of a graph is then <math>(\{A,B,C\},\{(A,B),(B,C),(A,C)\})</math>, for which <math>V=\{A,B,C\}</math> and <math>E=\{(A,B),(B,C),(A,C)\}</math>. This graph has vertices <math>A</math>, <math>B</math>, and <math>C</math>, an edge from <math>A</math> to <math>B</math>, an edge from <math>B</math> to <math>C</math>, and an edge from <math>A</math> to <math>C</math>. Note: we can write <math>(A,B) \in E(G)</math> to indicate that there exists an edge from <math>A</math> to <math>B</math>. However, the notation <math>(A,B) \in G</math> is incorrect. | * A graph is an ordered pair of two sets: <math>V</math> and <math>E</math>. The former is the set of vertices, and the latter the set of edges. We can write <math>G = (V,E)</math> to indicate that the graph <math>G</math> has vertex set <math>V</math> and edge set <math>E</math>. Also, given some graph <math>G</math>, <math>V(G)</math> is the vertex set of <math>G</math>, and <math>E(G)</math> is the edge set of <math>G</math>. An example of a graph is then <math>(\{A,B,C\},\{(A,B),(B,C),(A,C)\})</math>, for which <math>V=\{A,B,C\}</math> and <math>E=\{(A,B),(B,C),(A,C)\}</math>. This graph has vertices <math>A</math>, <math>B</math>, and <math>C</math>, an edge from <math>A</math> to <math>B</math>, an edge from <math>B</math> to <math>C</math>, and an edge from <math>A</math> to <math>C</math>. Note: we can write <math>(A,B) \in E(G)</math> to indicate that there exists an edge from <math>A</math> to <math>B</math>. However, the notation <math>(A,B) \in G</math> is incorrect. | ||
* The number of vertices in graph <math>G</math> is denoted <math>|V(G)|</math> (the size of the vertex set), and the number of edges <math>|E(G)|</math> (the size of the edge set). When discussing asymptotic performance, however, we generally write just <math>V</math> and <math>E</math>. | * The number of vertices in graph <math>G</math> is denoted <math>|V(G)|</math> (the size of the vertex set), and the number of edges <math>|E(G)|</math> (the size of the edge set). When discussing asymptotic performance, however, we generally write just <math>V</math> and <math>E</math>. | ||
| + | * The weight of an edge from vertex ''u'' to vertex ''v'' is regarded as the value of a ''cost function'' which should be denoted by a sensible name such as <code>wt</code>, hence we have <code>wt(u,v)</code> and so on. A weighted graph is then regarded as the tuple <math>(V,E,\mathrm{wt})</math>. | ||
| + | |||
| + | ==Coding style== | ||
| + | Blocks of code written in real programming languages should be enclosed in <nowiki><syntaxhighlight> ... </syntaxhighlight></nowiki> blocks. A list of supported languages can be found [http://www.mediawiki.org/wiki/Extension:SyntaxHighlight_GeSHi here]. Longer implementations of algorithms described in articles should be placed in a "subarticle" (''e.g.'', Foo/Bar.cpp). | ||
| + | |||
| + | Avoid choosing programming languages that programmers and computer scientists would not ordinarily use for implementing complex algorithms. C, C++, Pascal, and Java are preferable; they are the languages most often used in algorithmic programming contests, and they are the languages in which Sedgewick's ''Algorithms'' is available. C#, Python, LISP and its derivatives, Haskell, and ML-derived languages are acceptable. Try to stay away from PHP, Perl, VB, JavaScript, and assembly language (yes, I know Knuth uses assembly language, but still). Specialized programming languages such as Maple and MATLAB are sometimes justifiable but should not be used in general. | ||
| + | |||
| + | Because you are expected to choose a language that a programmer with a primarily algorithmic (rather than development-based) background would be somewhat familiar with, you can assume that the reader knows the language fairly well, so write code idiomatically whenever possible. It is not necessary to adhere to any particular style site-wide; it's okay for some articles to have beginning curly braces on the following line and others to have them on the same line, but try to be consistent within individual articles. | ||
Latest revision as of 21:15, 20 November 2011
This page documents some conventions to be followed when writing articles on PEGWiki. These are not binding policy on PEGWiki, but following them should minimize confusion and promote consistency across articles. You won't get in trouble for not following them, but what you write is likely to be slightly modified to conform with these conventions if it doesn't initially. If you see arcane or unfamiliar notation anywhere in an article, but especially in a pseudocode block, you may find its meaning here. Changes to these conventions should be discussed on the talk page.
Contents
Pseudocode conventions
Both text-mode and math-mode
- Structure should be indicated by indentation, as in Python. Adding braces
{}as in C or words such asbeginandendas in Pascal would introduce unnecessary clutter into pseudocode blocks. Do not use tabs for indentation. Five spaces is a good guideline. (In LaTeX pseudocode, this means five full-width spaces (a full-width space is "\").) - The
for,if/else, andwhilestatements should not be followed by words like "do" or "then", as in Pascal, but should stand alone, as in C; pseudocode is intended for humans, not machines. - Similarly, statements should not end in semicolons.
- Indices into arrays should be placed in square brackets,
[]. The Pascal convention of separating indices by commas is preferred to the C convention of having a separate set of brackets for each index (simply by virtue of being nicer and more intuitive), but the latter may be occasionally appropriate to reinforce the interpretation of the array's structure. Use your common sense. - Parameter lists should be enclosed in parentheses,
(), and parameters should be separated by commas. - A function header should contain with the word
function, the function's name, and the function's parameter list, in that order, as in PHP or JavaScript. The body of a function should be indented. - If something is not a real command, e.g.
inputorprint, it should not be written like a function (its parameter list should not have parentheses). - Object-oriented code should be used wherever appropriate, and nowhere else. The members of an object should be indicated by the dot operator
.. For example, it makes sense to represent a data structure as an object (which encapsulates the structure's data). However, please do not wrap an entire algorithm in an object as would be done in Java; that is pointless and only leads to clutter. - The mod operator should never return a negative result; the number-theoretic convention of always yielding a non-negative integer should be followed, as in Scheme.
Text-mode only
- Variable assignment should occur through the use of a single equals sign,
=, although the Pascal notation of:=is also acceptable. - Equality testing should also occur through the use of a single equals sign,
=, but is distinguished from variable assignment by context. For example, if it is preceded byif, it is an equality test, and if it stands alone, it is an assignment. The C notation of==should be avoided. - The symbols
<=,>=, and<>are equally acceptable as their single-symbol Unicode counterparts≤,≥, and≠, but in most other cases a Unicode symbol should be used whenever both necessary and possible. For example,oofor∞is unacceptable. - Variables (and named constants) from pseudocode blocks which are referenced in the article text should be in italics; all other items, such as functions and literal constants, should be
monospaced. The exception is literal numerical constants; it is acceptable not to format them specially, since they cause no confusion.
Math-mode only
- The LaTeX
\sqrtcommand is almost always preferable to typing out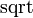 .
. - The vinculum (horizontal bar) to indicate division (produced by the
\fraccommand) is usually best, but if the numerator or denominator is complex, a single slash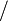 is preferable when it improves readability or overall aesthetic appeal.
is preferable when it improves readability or overall aesthetic appeal. - Exponentiation should always occur in the form
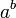 rather than in the form
rather than in the form  ^
^ . When the exponent is so complex that superscripting makes the expression look ugly, use a temporary variable for the exponent. The exception is when the base is
. When the exponent is so complex that superscripting makes the expression look ugly, use a temporary variable for the exponent. The exception is when the base is  : you can replace
: you can replace 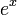 with
with 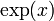 in that case.
in that case. - Actual words, such as "if" and "and", should not be italicized. Use the
\mathrmfunction to de-italicize them. - Equality testing should occur through the
 symbol.
symbol. - Variable assignment should occur through the
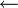 symbol (LaTeX code:
symbol (LaTeX code: \gets)
Technical notation
- Items enclosed in braces
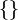 and separated by commas form a set or multiset. For example,
and separated by commas form a set or multiset. For example, 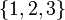 is a set containing the elements 1, 2, and 3. Normally they form a set; they form a multiset if stated otherwise. The difference is that a set contains no duplicate elements. Sets and multisets should be typed: that is, a set or multiset should not contain elements of different types. However, a set/multiset may itself contain sets/multisets, or any other kind of item.
is a set containing the elements 1, 2, and 3. Normally they form a set; they form a multiset if stated otherwise. The difference is that a set contains no duplicate elements. Sets and multisets should be typed: that is, a set or multiset should not contain elements of different types. However, a set/multiset may itself contain sets/multisets, or any other kind of item. - A set/multiset that contains no elements is denoted ∅ (LaTeX:
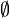 ).
). - A set/multiset that contains all elements of a given type is denoted
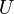 , the universal set. The type can generally be inferred from context.
, the universal set. The type can generally be inferred from context. - Items enclosed in parentheses
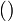 and separated by commas form a tuple. For example,
and separated by commas form a tuple. For example, 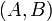 is an ordered pair (a tuple with two elements). Tuples, unlike sets and multisets, may contain elements of different types, and, again unlike sets and multisets, they have a fixed size.
is an ordered pair (a tuple with two elements). Tuples, unlike sets and multisets, may contain elements of different types, and, again unlike sets and multisets, they have a fixed size. - Equality of tuples is denoted by an equals sign,
 . Two tuples are equal if and only if they are equal in size and all corresponding pairs of elements are equal; hence,
. Two tuples are equal if and only if they are equal in size and all corresponding pairs of elements are equal; hence, 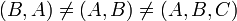 .
. - The symbol ∈ means "is a member of", and ∉ means "is not a member of ".
- The union of two sets or multisets
 and
and  is denoted
is denoted 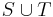 , their intersection
, their intersection 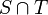 , and their difference
, and their difference 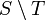 .
. - The size or cardinality of a set or multiset
 is denoted
is denoted 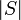 .
. - The symbols
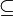 ,
, 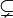 ,
, 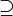 , and
, and 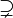 denote subset, proper subset, superset, and proper superset, respectively. The symbols
denote subset, proper subset, superset, and proper superset, respectively. The symbols 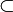 and
and 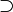 are ambiguous and should be avoided. These relations are defined on multisets similarly to how they are defined on sets.
are ambiguous and should be avoided. These relations are defined on multisets similarly to how they are defined on sets. - The Cartesian product of two sets or multisets
 and
and  is denoted
is denoted 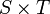 .
. - The complement of a set is denoted
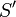 ; the complement is not defined on multisets.
; the complement is not defined on multisets. - The sum of two multisets
 and
and  is denoted
is denoted 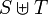 ; this is not defined on ordinary sets.
; this is not defined on ordinary sets. - A list is written like a set but with square brackets,
![[\,]](/wiki/images/math/3/b/1/3b12bb11542226fbabbed444e20f4110.png) . It is an ordered collection of elements of the same type. A list is like a set in that its size is not fixed but elements can be added and removed. It is like a tuple in that two lists are considered equal if and only if they are of the same size and all pairs of corresponding elements are equal. Hence,
. It is an ordered collection of elements of the same type. A list is like a set in that its size is not fixed but elements can be added and removed. It is like a tuple in that two lists are considered equal if and only if they are of the same size and all pairs of corresponding elements are equal. Hence, ![[1,2,3] \neq [1,3,2]](/wiki/images/math/3/1/f/31f409e7879362921fd401e0e909d846.png) , as their elements are in different orders.
, as their elements are in different orders. - Two lists written with a plus sign between them represents the concatenation of the two lists: hence,
![[1,2] + [3,4] = [1,2,3,4]](/wiki/images/math/d/d/6/dd6eaac5d753ed2182601023c54d392a.png) . Notice that concatenation is noncommutative.
. Notice that concatenation is noncommutative. -
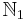 represents the positive integers.
represents the positive integers. 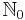 represents the non-negative integers. Unless the intended meaning is absolutely clear from context, please use a subscript 0 or 1 instead of simply writing
represents the non-negative integers. Unless the intended meaning is absolutely clear from context, please use a subscript 0 or 1 instead of simply writing 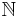 .
.
Graph theory
- Vertices in graphs should be given either non-negative integers or letters as labels; letters however must be italicized except when in code blocks. Subscripts on letters are okay: we might for example label the vertices of a bipartite graph as
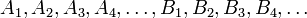 , in which edges exist only between
, in which edges exist only between  s and
s and  s. Subscripts on numbers, however, are not.
s. Subscripts on numbers, however, are not. - An edge in a directed graph is an ordered pair of vertices. For example, if a graph has an edge from
 to
to  , then this can be described as
, then this can be described as 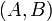 . An edge in an undirected graph is an unordered pair, or a set containing two vertices: for example,
. An edge in an undirected graph is an unordered pair, or a set containing two vertices: for example, 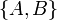 . (If self-loops are allowed, then it's actually a multiset.)
. (If self-loops are allowed, then it's actually a multiset.) - A graph is an ordered pair of two sets:
 and
and 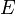 . The former is the set of vertices, and the latter the set of edges. We can write
. The former is the set of vertices, and the latter the set of edges. We can write 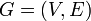 to indicate that the graph
to indicate that the graph  has vertex set
has vertex set  and edge set
and edge set 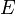 . Also, given some graph
. Also, given some graph  ,
, 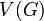 is the vertex set of
is the vertex set of  , and
, and 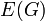 is the edge set of
is the edge set of  . An example of a graph is then
. An example of a graph is then 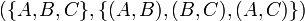 , for which
, for which 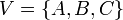 and
and 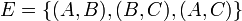 . This graph has vertices
. This graph has vertices  ,
,  , and
, and  , an edge from
, an edge from  to
to  , an edge from
, an edge from  to
to  , and an edge from
, and an edge from  to
to  . Note: we can write
. Note: we can write 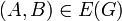 to indicate that there exists an edge from
to indicate that there exists an edge from  to
to  . However, the notation
. However, the notation 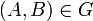 is incorrect.
is incorrect. - The number of vertices in graph
 is denoted
is denoted 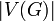 (the size of the vertex set), and the number of edges
(the size of the vertex set), and the number of edges 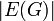 (the size of the edge set). When discussing asymptotic performance, however, we generally write just
(the size of the edge set). When discussing asymptotic performance, however, we generally write just  and
and 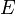 .
. - The weight of an edge from vertex u to vertex v is regarded as the value of a cost function which should be denoted by a sensible name such as
wt, hence we havewt(u,v)and so on. A weighted graph is then regarded as the tuple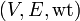 .
.
Coding style
Blocks of code written in real programming languages should be enclosed in <syntaxhighlight> ... </syntaxhighlight> blocks. A list of supported languages can be found here. Longer implementations of algorithms described in articles should be placed in a "subarticle" (e.g., Foo/Bar.cpp).
Avoid choosing programming languages that programmers and computer scientists would not ordinarily use for implementing complex algorithms. C, C++, Pascal, and Java are preferable; they are the languages most often used in algorithmic programming contests, and they are the languages in which Sedgewick's Algorithms is available. C#, Python, LISP and its derivatives, Haskell, and ML-derived languages are acceptable. Try to stay away from PHP, Perl, VB, JavaScript, and assembly language (yes, I know Knuth uses assembly language, but still). Specialized programming languages such as Maple and MATLAB are sometimes justifiable but should not be used in general.
Because you are expected to choose a language that a programmer with a primarily algorithmic (rather than development-based) background would be somewhat familiar with, you can assume that the reader knows the language fairly well, so write code idiomatically whenever possible. It is not necessary to adhere to any particular style site-wide; it's okay for some articles to have beginning curly braces on the following line and others to have them on the same line, but try to be consistent within individual articles.