Difference between revisions of "Dijkstra's algorithm"
(Created page with ''''Dijkstra's algorithm''' finds single-source shortest paths in a directed graph with non-negative edge weights. (When negative-weight edges are allowed, the […') |
|||
| (11 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | '''Dijkstra's algorithm''' finds [[ | + | '''Dijkstra's algorithm''' finds [[Shortest_path#Single-source_shortest_paths|single-source shortest paths]] in a directed graph with non-negative edge weights. (When negative-weight edges are allowed, the [[Bellman–Ford algorithm]] must be used instead.) It is the algorithm of choice for solving this problem, because it is easy to understand, relatively easy to code, and, so far, the fastest algorithm known for solving this problem in the general case. In sparse graphs, running it once on every vertex to generate all-pairs shortest paths is faster than solving the same problem with the [[Floyd–Warshall algorithm]]. (The precise time complexity of Dijkstra's depends on the nature of the data structures used; read on.) |
| − | =Theory of the algorithm= | + | ==Theory of the algorithm== |
| − | Dijkstra's may be characterized as a [[greedy algorithm]], which builds the shortest-paths tree one edge at a time, adding vertices in non-decreasing order of their distance from the source. That is, in each step of the algorithm, we will find the next-closest vertex to the source. (If there is a tie, it does not matter which one is chosen.) | + | Dijkstra's may be characterized as a [[greedy algorithm]], which builds the shortest-paths tree one edge at a time, adding vertices in non-decreasing order of their distance from the source. That is, in each step of the algorithm, we will find the next-closest vertex to the source. (If there is a tie, it does not matter which one is chosen.) We assume below that all nodes are reachable from the source. (If you find the two sections below too difficult, skip them.) |
| − | ==Lemma | + | ===Lemma=== |
| − | + | Suppose that we are given a set <math>T</math> of vertices, containing the source <i>s</i>. We shall call a path <i>admissible</i> if it starts at <i>s</i>, proceeds through a sequence of vertices contained within <math>T</math>, and ends with a single non-<math>T</math> vertex. We claim that there exists an admissible path such that no other path from <i>s</i> to a non-<math>T</math> vertex is shorter. | |
| − | + | ''Proof'': This consists of nothing but a series of observations. First, any path from <i>s</i> to a vertex <i>v</i> outside <math>T</math> contains at least one edge from a vertex in <math>T</math> to one outside, since <i>s</i> ∈ <math>T</math>. Second, if the first such edge encountered along the path from <i>s</i> is not the last edge in the path, we can "cut off" the path at that point to obtain a path from <i>s</i> out of <math>T</math> that is not longer (since all edges have non-negative weights). Third, if the sub-path from <i>s</i> to the last vertex in <math>T</math>, denoted <i>u</i>, is not itself a shortest path from <i>s</i> to <i>u</i>, the length of the whole path may be decreased by substituting a shortest path from <i>s</i> to <i>u</i> for the current one. Now, suppose the opposite of what we want to prove: the shortest path from <i>s</i> out of <math>T</math>, or all the shortest paths from <i>s</i> out of <math>T</math>, is/are inadmissible. Then we may construct an admissible path using the three observations above which is not longer, a contradiction. | |
| − | ==The algorithm== | + | ===The algorithm=== |
| − | The preceding Lemma should give us an idea of how to proceed. We start with only the source vertex in the shortest-paths tree; its distance to itself is obviously zero. Then, we repeatedly apply the Lemma | + | The preceding Lemma should give us an idea of how to proceed. We start with only the source vertex in the shortest-paths tree (<math>T</math> is merely the vertex set of the partial shortest-paths tree); its distance to itself is obviously zero. Then, we repeatedly apply the Lemma by considering all admissible paths and finding the shortest. To do this we consider all edges that lead from a <math>T</math> vertex <i>u</i> to a non-<math>T</math> vertex <i>v</i>. Concatenating the <i>s</i>-<i>u</i> shortest path and the <i>u</i>-<i>v</i> edge yields an admissible path whose length is the sum of the length of the already-known <i>s</i>-<i>u</i> path and the weight of the <i>u</i>-<i>v</i> edge. The edge and vertex <i>v</i> at the very end of the shortest admissible path are added to the shortest-paths tree (and thus <i>v</i> is added to <math>T</math>); as no path from <i>s</i> to a non-<math>T</math> vertex can be shorter, we are justified in claiming that <i>v</i> is the closest non-<math>T</math> vertex to <i>s</i>, and that its distance from <i>s</i> is the shortest obtainable from an admissible path currently. This method of extending the shortest-paths tree by one vertex is repeated until all vertices have been added, and induction proves the algorithm's validity. (The extension can always be performed because otherwise the remaining vertices would be unreachable from the source, a contradiction.) |
| − | + | ==Implementation 1== | |
| + | As the previous sections are a bit heavy, here is some pseudocode for Dijkstra's algorithm: | ||
<pre> | <pre> | ||
| − | input G, | + | input G,s |
| − | for each | + | for each v ∈ V(G) |
| − | let dist[ | + | let dist[v] = ∞ |
| − | let dist[ | + | let dist[s] = 0 |
| − | + | let T = ∅ | |
| − | for each ( | + | while T ≠ V(G) |
| − | dist[w] = min(dist[w],dist[ | + | let v ∈ V(G)\T such that dist[v] is minimal |
| − | + | add v to T | |
| − | + | for each w ∈ V(G) such that (v,w) ∈ E(G) | |
| − | + | dist[w] = min(dist[w],dist[v]+wt(v,w)) | |
</pre> | </pre> | ||
| − | + | Following the completion of this code, the <code>dist</code> array will contain the minimum path lengths from <code>s</code> to each vertex, or <math>\infty</math> if no such path exists for a given vertex. | |
| − | = | + | ===Analysis=== |
| − | == | + | In each iteration the inner loop will add a vertex to <math>T</math>, so at most <math>V</math> iterations will take place; in each one it takes <math>O(V)</math> time to find the vertex with the minimal <code>dist</code> entry. The inner loop executes at most <math>2E</math> times, since it considers each edge at most twice (once from each endpoint). A naive implementation therefore takes <math>O(E+V^2)</math> time. In a dense graph, this is asymptotically optimal. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | == | + | ==Implementation 2== |
| − | + | This implementation allows us to make optimizations, and more closely follows the theory, but requires a data structure <code>Q</code>: | |
| − | < | + | <pre> |
| − | + | input G,s | |
| − | -- | + | for each v ∈ V(G) |
| + | let dist[v] = ∞ | ||
| + | add (s,0) to Q | ||
| + | while Q is nonempty | ||
| + | let (v,d) ∈ Q such that d is minimal | ||
| + | remove (v,d) from Q | ||
| + | if dist[v] = ∞ | ||
| + | dist[v] = d | ||
| + | for each w ∈ V(G) such that (v,w) ∈ E(G) | ||
| + | add (w,d+wt(v,w)) to Q | ||
| + | </pre> | ||
| + | Each iteration of the main loop is again an iteration of the Lemma. <math>T</math> is now implicit; it consists of all vertices with current distance (<code>dist</code> value) less than infinity. The data structure <code>Q</code> contains nodes that should potentially be explored next; it contains all nodes that are reachable from a single edge out of <math>T</math>. Selecting the closest one at each iteration, we eventually explore the entire connected component and compute all shortest paths. | ||
| + | |||
| + | ===Analysis=== | ||
| + | The data structure <code>Q</code> is a priority queue ADT. If we use the [[binary heap]] implementation, then insertion and removal both take <math>O(\log N)</math> time, whereas querying the minimal element takes constant time. At most <math>2E</math> edges are inserted and at most <math>V</math> deletions occur, which gives a time bound of <math>O((E+V) \log (2E))</math>. We assume the graph has no duplicate edges, so that <math>E < V^2</math>, and then <math>\log (2E) < 2 \log V + \log 2</math>, giving the oft-quoted <math>O((E+V) \log V)</math> time bound. Hence this implementation outperforms the first in a sparse graph, and running it once per vertex to obtain all-pairs shortest paths outperforms the [[Floyd–Warshall algorithm]] in sparse graphs. | ||
| + | |||
| + | Using a [[Fibonacci heap]] implementation, which supports amortized constant time insertion, we can improve this to <math>O(E + V \log V)</math>. | ||
| + | |||
| + | ==Singly constrained variant== | ||
| + | Dijkstra's algorithm can solve the ''singly constrained shortest path problem''. In this problem, each edge has ''two'' nonnegative weights, a length and a cost, and we wish to minimize path length subject to the constraint that the total cost must not exceed <math>C</math>. The code looks very similar: | ||
| + | <pre> | ||
| + | input G,s | ||
| + | for each v ∈ V(G) | ||
| + | let dist[v] = ∞ | ||
| + | let mincost[v] = ∞ | ||
| + | add (s,0,0) to Q | ||
| + | while Q is nonempty | ||
| + | let (v,d,c) ∈ Q such that c is minimal | ||
| + | remove (v,d,c) from Q | ||
| + | if d < dist[v] | ||
| + | dist[v] = d | ||
| + | for each w ∈ V(G) such that (v,w) ∈ E(G) and c + cost(v,w) ≤ C | ||
| + | add (w,d+wt(v,w),c+cost(v,w)) to Q | ||
| + | </pre> | ||
| + | Following completion of this code, the <code>dist</code> array holds the minimum path lengths found, and the <code>mincost</code> array holds the cost, for each vertex, required to achieve the minimum distance. | ||
| + | |||
| + | ==References== | ||
| + | * Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001). "Section 24.3: Dijkstra's algorithm". ''Introduction to Algorithms'' (Second ed.). MIT Press and McGraw-Hill. pp. 595–601. ISBN 0-262-03293-7. | ||
| + | |||
| + | [[Category:Algorithms]] | ||
| + | [[Category:Graph theory]] | ||
Latest revision as of 05:45, 31 May 2011
Dijkstra's algorithm finds single-source shortest paths in a directed graph with non-negative edge weights. (When negative-weight edges are allowed, the Bellman–Ford algorithm must be used instead.) It is the algorithm of choice for solving this problem, because it is easy to understand, relatively easy to code, and, so far, the fastest algorithm known for solving this problem in the general case. In sparse graphs, running it once on every vertex to generate all-pairs shortest paths is faster than solving the same problem with the Floyd–Warshall algorithm. (The precise time complexity of Dijkstra's depends on the nature of the data structures used; read on.)
Contents
Theory of the algorithm
Dijkstra's may be characterized as a greedy algorithm, which builds the shortest-paths tree one edge at a time, adding vertices in non-decreasing order of their distance from the source. That is, in each step of the algorithm, we will find the next-closest vertex to the source. (If there is a tie, it does not matter which one is chosen.) We assume below that all nodes are reachable from the source. (If you find the two sections below too difficult, skip them.)
Lemma
Suppose that we are given a set  of vertices, containing the source s. We shall call a path admissible if it starts at s, proceeds through a sequence of vertices contained within
of vertices, containing the source s. We shall call a path admissible if it starts at s, proceeds through a sequence of vertices contained within  , and ends with a single non-
, and ends with a single non- vertex. We claim that there exists an admissible path such that no other path from s to a non-
vertex. We claim that there exists an admissible path such that no other path from s to a non- vertex is shorter.
vertex is shorter.
Proof: This consists of nothing but a series of observations. First, any path from s to a vertex v outside  contains at least one edge from a vertex in
contains at least one edge from a vertex in  to one outside, since s ∈
to one outside, since s ∈  . Second, if the first such edge encountered along the path from s is not the last edge in the path, we can "cut off" the path at that point to obtain a path from s out of
. Second, if the first such edge encountered along the path from s is not the last edge in the path, we can "cut off" the path at that point to obtain a path from s out of  that is not longer (since all edges have non-negative weights). Third, if the sub-path from s to the last vertex in
that is not longer (since all edges have non-negative weights). Third, if the sub-path from s to the last vertex in  , denoted u, is not itself a shortest path from s to u, the length of the whole path may be decreased by substituting a shortest path from s to u for the current one. Now, suppose the opposite of what we want to prove: the shortest path from s out of
, denoted u, is not itself a shortest path from s to u, the length of the whole path may be decreased by substituting a shortest path from s to u for the current one. Now, suppose the opposite of what we want to prove: the shortest path from s out of  , or all the shortest paths from s out of
, or all the shortest paths from s out of  , is/are inadmissible. Then we may construct an admissible path using the three observations above which is not longer, a contradiction.
, is/are inadmissible. Then we may construct an admissible path using the three observations above which is not longer, a contradiction.
The algorithm
The preceding Lemma should give us an idea of how to proceed. We start with only the source vertex in the shortest-paths tree ( is merely the vertex set of the partial shortest-paths tree); its distance to itself is obviously zero. Then, we repeatedly apply the Lemma by considering all admissible paths and finding the shortest. To do this we consider all edges that lead from a
is merely the vertex set of the partial shortest-paths tree); its distance to itself is obviously zero. Then, we repeatedly apply the Lemma by considering all admissible paths and finding the shortest. To do this we consider all edges that lead from a  vertex u to a non-
vertex u to a non- vertex v. Concatenating the s-u shortest path and the u-v edge yields an admissible path whose length is the sum of the length of the already-known s-u path and the weight of the u-v edge. The edge and vertex v at the very end of the shortest admissible path are added to the shortest-paths tree (and thus v is added to
vertex v. Concatenating the s-u shortest path and the u-v edge yields an admissible path whose length is the sum of the length of the already-known s-u path and the weight of the u-v edge. The edge and vertex v at the very end of the shortest admissible path are added to the shortest-paths tree (and thus v is added to  ); as no path from s to a non-
); as no path from s to a non- vertex can be shorter, we are justified in claiming that v is the closest non-
vertex can be shorter, we are justified in claiming that v is the closest non- vertex to s, and that its distance from s is the shortest obtainable from an admissible path currently. This method of extending the shortest-paths tree by one vertex is repeated until all vertices have been added, and induction proves the algorithm's validity. (The extension can always be performed because otherwise the remaining vertices would be unreachable from the source, a contradiction.)
vertex to s, and that its distance from s is the shortest obtainable from an admissible path currently. This method of extending the shortest-paths tree by one vertex is repeated until all vertices have been added, and induction proves the algorithm's validity. (The extension can always be performed because otherwise the remaining vertices would be unreachable from the source, a contradiction.)
Implementation 1
As the previous sections are a bit heavy, here is some pseudocode for Dijkstra's algorithm:
input G,s
for each v ∈ V(G)
let dist[v] = ∞
let dist[s] = 0
let T = ∅
while T ≠ V(G)
let v ∈ V(G)\T such that dist[v] is minimal
add v to T
for each w ∈ V(G) such that (v,w) ∈ E(G)
dist[w] = min(dist[w],dist[v]+wt(v,w))
Following the completion of this code, the dist array will contain the minimum path lengths from s to each vertex, or 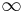 if no such path exists for a given vertex.
if no such path exists for a given vertex.
Analysis
In each iteration the inner loop will add a vertex to  , so at most
, so at most  iterations will take place; in each one it takes
iterations will take place; in each one it takes 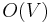 time to find the vertex with the minimal
time to find the vertex with the minimal dist entry. The inner loop executes at most 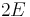 times, since it considers each edge at most twice (once from each endpoint). A naive implementation therefore takes
times, since it considers each edge at most twice (once from each endpoint). A naive implementation therefore takes 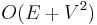 time. In a dense graph, this is asymptotically optimal.
time. In a dense graph, this is asymptotically optimal.
Implementation 2
This implementation allows us to make optimizations, and more closely follows the theory, but requires a data structure Q:
input G,s
for each v ∈ V(G)
let dist[v] = ∞
add (s,0) to Q
while Q is nonempty
let (v,d) ∈ Q such that d is minimal
remove (v,d) from Q
if dist[v] = ∞
dist[v] = d
for each w ∈ V(G) such that (v,w) ∈ E(G)
add (w,d+wt(v,w)) to Q
Each iteration of the main loop is again an iteration of the Lemma.  is now implicit; it consists of all vertices with current distance (
is now implicit; it consists of all vertices with current distance (dist value) less than infinity. The data structure Q contains nodes that should potentially be explored next; it contains all nodes that are reachable from a single edge out of  . Selecting the closest one at each iteration, we eventually explore the entire connected component and compute all shortest paths.
. Selecting the closest one at each iteration, we eventually explore the entire connected component and compute all shortest paths.
Analysis
The data structure Q is a priority queue ADT. If we use the binary heap implementation, then insertion and removal both take 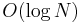 time, whereas querying the minimal element takes constant time. At most
time, whereas querying the minimal element takes constant time. At most 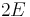 edges are inserted and at most
edges are inserted and at most  deletions occur, which gives a time bound of
deletions occur, which gives a time bound of 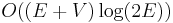 . We assume the graph has no duplicate edges, so that
. We assume the graph has no duplicate edges, so that 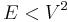 , and then
, and then 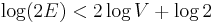 , giving the oft-quoted
, giving the oft-quoted 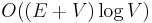 time bound. Hence this implementation outperforms the first in a sparse graph, and running it once per vertex to obtain all-pairs shortest paths outperforms the Floyd–Warshall algorithm in sparse graphs.
time bound. Hence this implementation outperforms the first in a sparse graph, and running it once per vertex to obtain all-pairs shortest paths outperforms the Floyd–Warshall algorithm in sparse graphs.
Using a Fibonacci heap implementation, which supports amortized constant time insertion, we can improve this to 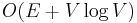 .
.
Singly constrained variant
Dijkstra's algorithm can solve the singly constrained shortest path problem. In this problem, each edge has two nonnegative weights, a length and a cost, and we wish to minimize path length subject to the constraint that the total cost must not exceed  . The code looks very similar:
. The code looks very similar:
input G,s
for each v ∈ V(G)
let dist[v] = ∞
let mincost[v] = ∞
add (s,0,0) to Q
while Q is nonempty
let (v,d,c) ∈ Q such that c is minimal
remove (v,d,c) from Q
if d < dist[v]
dist[v] = d
for each w ∈ V(G) such that (v,w) ∈ E(G) and c + cost(v,w) ≤ C
add (w,d+wt(v,w),c+cost(v,w)) to Q
Following completion of this code, the dist array holds the minimum path lengths found, and the mincost array holds the cost, for each vertex, required to achieve the minimum distance.
References
- Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001). "Section 24.3: Dijkstra's algorithm". Introduction to Algorithms (Second ed.). MIT Press and McGraw-Hill. pp. 595–601. ISBN 0-262-03293-7.