Topological sort

The topological sorting problem is the problem of determining a topological ordering of a digraph's vertices, that is, a list of the vertices such that an edge never exists from a vertex later in the list to a vertex earlier in the list.

Motivation

Topological sorting is perhaps best understood as the problem of dependency resolution. Examples are given here:

• To earn a degree, a student has to complete certain required courses. However, these cannot be taken in just any order; some of these courses are prerequisites for others. For example, the Introduction to Algorithms in Bioinformatics course may depend on the Introduction to Algorithms course, which may depend on the Introduction to Data Structures course, which may in turn depend on the Introduction to Programming course. This is a dependency relationship; taking later courses depends on taking prerequisite earlier courses. We can construct a graph in which each vertex is a course and a directed edge exists from $u$ to $v$ if and only if the course corresponding to $u$ is a prerequisite for the course corresponding to $v$. Topologically sorting this graph will give a possible order in which the courses may be taken (although it cannot, of course, be used to solve the more serious problem of scheduling conflicts).
• Large software applications are usually heavily modularized, where, generally, each module is a chunk of code of manageable size containing a simple group of related functions stored in a single file or a small number of files. These modules may depend on simpler modules, which may in turn depend on simpler modules, and so on down. For example, the compiler gcc may depend on the arithmetic library gmp, which may depend on the macro language m4, which may depend on the C standard library libc. We cannot compile a module until all its dependencies have already been compiled. If each module is a vertex and an edge exists from one vertex to another if and only if the latter's module depends on the former's, then topologically sorting this graph gives a valid order in which we may compile all the modules. (The program /usr/bin/tsort was provided on many UNIX-based systems exactly for this purpose; it has been superseded by make, but it still exists on some modern systems.)
• In some video games, each level consists of exploring a particular part of the world map. There is no preset order on how to explore the map, but some areas may not be explored right away because they depend on "earlier" areas having been explored (and presumably "beaten"). We let each area of the map be a vertex and let there be an edge from one vertex to another if the former's area must be explored before the latter's. A topological ordering of this graph corresponds to a valid order in which the map may be explored.

Existence of a solution

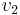We first note that being a DAG is necessary for a digraph to have a topological ordering. This is not hard to see; if the graph contains a cycle, $v_1 v_2 ... v_n v_1$, then $v_2$ must occur after 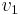$v_1$ in the topological ordering, 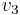$v_3$ must occur after 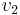$v_2$, and so on, but then 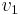$v_1$ must occur after 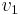$v_1$, leading to the absurd conclusion that 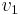$v_1$ must occur after itself in the list. Intuitively, if a cyclic dependency exists among a set of tasks, none of those tasks can ever be executed.

The next question is whether this condition is also sufficient. That is, is it true that a digraph may be topologically ordered if and only if it is a DAG? The answer is yes.

Theorem: Every DAG may be topologically ordered.

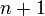Proof: By induction on the number of vertices. Clearly, a DAG with one vertex may be topologically ordered; the list in this case consists only of the vertex itself. Now, suppose that any DAG with $n$ vertices may be ordered, and now consider any DAG with $n+1$ vertices. Recall that every DAG has at least one source. We let this be the first entry in our list. The subgraph left behind, which has $n$ vertices, is still acyclic; obviously cycles cannot be introduced by removing edges. By the inductive hypothesis, we can topologically order this subgraph. 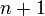Then, we append the topological ordering of this subgraph to the end of our current list, to obtain a list of vertices of the original $n+1$-vertex graph with the source in the first position. Now, given any two vertices $u$ and $v$ on the list, where, without loss of generality, $u$ precedes $v$, either $u$ is the first entry (the source), in which case there is obviously no $v$-$u$ edge, or $u$ and $v$ are both not the first entry, in which case they must be properly ordered as they belong to the topologically ordered tail of the list. 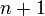Therefore this new list of $n+1$ vertices is a topological ordering of the 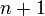$n+1$-vertex graph. $_\blacksquare$

Uniqueness

In general, the topological ordering is not unique; there may be several different orders in which the graph may be traversed that satisfy the topological ordering property. It is, however, unique if and only if the partial order represented by the DAG is in fact a total order; that is, when the DAG has a Hamiltonian path, or, equivalently, the transitive closure of the DAG is the complete graph.

Algorithm

The algorithm for generating a topological ordering is embedded in the proof of the Theorem above:

1. Start with an empty list.
2. Find a source of the DAG. Add this vertex to the end of the list.
3. Remove the vertex and all incident edges.
4. If the DAG is nonempty, go back to step 2.

After the termination of this procedure, the list will contain a topological ordering of the DAG.

In order to implement this algorithm efficiently, we will not actually remove vertices from the graph in step 3, since this is a computationally expensive operation if the graph is represented as an adjacency matrix or an adjacency list. Nor will we scan through the entire graph each time step 2 is executed in order to find a source; this, too, is computationally expensive. Instead, we make the following observations, in this order:

1. A vertex is a source if and only if its in-degree is zero.
2. If a vertex is not originally a source, it will become one after all its incoming edges have been deleted. An incoming edge is deleted only when the vertex at the other side is removed.
3. Suppose we know where all the sources are in the DAG, and we execute steps 2 and 3 once. After this, the only vertices that might become sources are the ones with an incoming edge from the vertex just removed.

Here, then, is a realistic implementation:

for u ∈ V(G)
    indegree[u] ← 0
for (u,v) ∈ E(G)
    indegree[v] ← indegree[v]+1
let C be an empty container
let L be an empty list
for u ∈ V(G)
    if indegree[u] = 0
        insert u into C
while C is not empty
    u ← some element of C
    remove u from C
    add u to the end of L
    for each v ∈ V(G) such that (u,v) ∈ E(G)
        indegree[v] ← indegree[v]-1
        if indegree[v] = 0
            insert v into C
if |L| < |V(G)|
    print "Error: graph contains a cycle"

To implement this efficiently, we will need to be able to iterate through the neighbors of a vertex efficiently. This is best done using an adjacency list. Also, C should be a stack or a queue, so that insertion and removal of elements can be accomplished in constant time. With that, notice that the first for loop takes 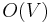$O(V)$ time, the second 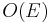$O(E)$ time, and the third 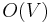$O(V)$ time; the while loop runs once for each vertex removed from the container, which only occurs 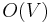$O(V)$ times, since each vertex is inserted at most once (either at the beginning or just after the last incoming edge is removed), and each edge is examined at most once in the while loop (when the vertex it leaves is popped). Overall, then, this algorithm takes 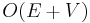$O(E+V)$ time (linear).

The algorithm will always find a topological ordering if one exists. If one does not exist, the list L will not be fully populated, and an error message will be printed.

The topological ordering will be unique if and only if C contains exactly one vertex at the beginning of each iteration of the while loop. The proof is left as an exercise to the reader.

Theorem: A topological ordering can also be obtained by running depth-first search and then reversing the postordering generated.

Proof: This is equivalent to the statement that if the edge $u-v$ exists then $u$ has a higher postorder number than $v$. So consider the DFS tree. If $u$ is an ancestor of $v$, then $u$ has a higher postorder number, as desired. If $u$ is a descendant of $v$ in the DFS tree, then a cycle exists from $u$ back to itself, a contradiction. And if neither $u$ nor $v$ is an ancestor of the other, then $u-v$ is a cross edge, and $u$ has a higher postorder number, as desired. $_\blacksquare$

External links

• Project File Dependencies
• Dependency Problems