Bellman–Ford algorithm

The Bellman-Ford algorithm finds single-source shortest paths in a directed, weighted graph which contains no negative-weight cycles. That is, unlike Dijkstra's algorithm, it is guaranteed to correctly compute shortest paths even when some edge weights are negative. (Note however that it is still a requirement that no negative-weight cycle occurs; finding shortest paths in such a graph becomes either meaningless if non-simple paths are allowed, or computationally difficult when they are not.) When single-source shortest paths are all that which is needed, and not all-pairs shortest paths, The Bellman–Ford algorithm, with time complexity 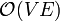$\mathcal{O}(VE)$, outperforms the Floyd–Warshall algorithm at 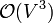$\mathcal{O}(V^3)$ in sparse graphs. It may also be combined with Dijkstra's algorithm to yield Johnson's algorithm, which again outperforms Floyd–Warshall in sparse graphs.

input G,v
for each u ∈ V(G)
     let dist[u] = ∞
let dist[v] = 0
for each i ∈ [1..V-1]
     for each (u,w) ∈ E(G)
          dist[w] = min(dist[w],dist[u]+wt(u,w))
for each (u,w) ∈ E(G)
     if dist[w] > dist[u]+wt(u,w)
          error "Graph contains negative-weight cycles"

G is the directed, weighted graph in question, and v the source. The output is the array dist; at the completion of the algorithm, dist[x] contains the shortest-path distance from v to x. If the graph contains a cycle of negative weight, an error message is generated to that effect.

Theory of the algorithm

The algorithm works by performing a series of relaxations. A relaxation occurs whenever the current shortest distance from node v to node w is improved because, by travelling from v to some intermediate vertex u, and then from u to w, a shorter path is obtained. (Floyd–Warshall and Dijkstra's algorithms rely upon this same technique.) The key is that, after n passes of the main loop in Bellman–Ford have completed, at least n+1 of the shortest-path distances in dist are correct. (We consider all pairs of vertices to be connected, so that all "missing" edges are assigned a weight of positive infinity.)

Proof of correctness for graphs containing no negative-weight cycles

We proceed by induction:

• When 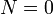$N=0$, there is at least 1 correct entry in dist, the one stating that the distance from the source to itself is zero.
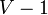• Now suppose that $N$ passes have occurred and that we know the shortest-path distances from the source to $N+1$ of the vertices. 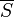Now, either $N$ is equal to $V-1$, and we are done, or the vertices may be partitioned into two sets: $S$, which contains $N+1$ vertices for which we already know shortest-path distances (with any $N+1$ being chosen if there are more than this number), and $\overline{S}$, which contains the rest. Now, since a shortest-paths tree exists (it always does when there are no negative-weight cycles; the proof is in the Shortest path article), there must exist some vertex w in 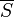$\overline{S}$ whose parent u in the shortest-paths tree is in $S$. Then, when the edge (u,w) is relaxed, the dist array will contain the correct shortest-path distance to w. 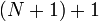Thus, after the next pass of the outer loop has occurred, $N+1$ passes will have occurred in total, and the shortest-path distances to at least $(N+1)+1$ vertices will be correctly known.

Thus, when a negative-weight cycle does not exist, after the main loop has finished, all distances in dist are correct. Now, if an edge (u,w) still exists such that dist[w] > dist[u]+wt(u,w), then the distances could not possibly have been correct, because relaxation of (u,w) would give a shorter path to w. Since this is a contradiction, the assumption of the non-existence of negative-weight cycles must be incorrect in this case. We see then that as long as there are no negative-weight cycles, the algorithm always computes all distances correctly and terminates successfully.

Proof of detection of negative-weight cycles

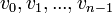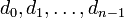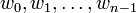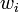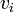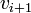Suppose vertices $v_0, v_1,..., v_{n-1}$ vertices form a negative-weight cycle, that at some point their entries in the dist array are $d_0, d_1,\ldots, d_{n-1}$, and that the numbers $w_0, w_1,\ldots, w_{n-1}$ represent the weights of edges in the cycle, where $w_i$ is the weight of the edge from $v_i$ to $v_{i+1}$. Now, because the cycle has negative weight, we know that 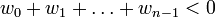$w_0+w_1+\ldots+w_{n-1}<0$. We show by contradiction that it is always possible to relax one of the edges.

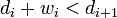Suppose we assume the opposite: that there exists no $i$ such that $d_i + w_i < d_{i+1}$. Then, we have 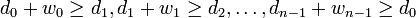$d_0 + w_0 \ge d_1, d_1 + w_1 \ge d_2,\ldots, d_{n-1} + w_{n-1} \ge d_0$. Adding yields 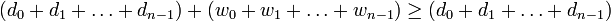$(d_0 + d_1 + \ldots + d_{n-1}) + (w_0 + w_1 + \ldots + w_{n-1}) \ge (d_0 + d_1 + \ldots + d_{n-1})$, which, after cancelling the 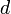$d$'s, is a contradiction. So our assumption must be false, and it must always be possible to relax at least one of the edges in a negative-weight cycle. Thus, if there is a negative-weight cycle, it will always be detected at the end of the algorithm, because at least one edge on that cycle must be capable of relaxation.

References

• Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Section 24.1: The Bellman-Ford algorithm, pp.588–592.