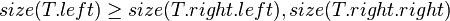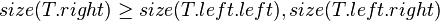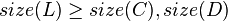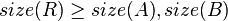Size Balanced Tree
A size balanced tree (SBT) is a self-balancing binary search tree first published by Chinese student Qifeng Chen in 2007. The tree is rebalanced by examining the sizes of each node's subtrees. Its abbreviation resulted in many nicknames given by Chinese informatics competitors, including "sha bi" tree (Chinese: 傻屄树; pinyin: shǎ bī shù; literally meaning "dumb cunt tree") and "super BT", which is a homophone to the Chinese term for snot (Chinese: 鼻涕; pinyin: bítì) suggesting that it is messy to implement. Contrary to what its nicknames suggest, this data structure can be very useful, and is also known to be easy to implement. Since the only extra piece of information that needs to be stored is sizes of the nodes (instead of other "useless" fields such as randomized weights in treaps or colours in red–black tress), this makes it very convenient to implement the select-by-rank and get-rank operations in dynamic order statistics problems. It supports standard binary search tree operations such as insertion, deletion, and searching in O(log n) time. According to Chen's paper, "this is the fastest known advanced binary search tree to date."
Properties
The size balanced tree examines each node's size (i.e. the number of nodes in the subtree rooted at that node) to determine when rotations should be performed. Each node  in the tree satisfies the following two properties:
in the tree satisfies the following two properties:
In other words, each child node of  is not smaller in size than the child nodes of its sibling. Clearly, we should consider the sizes of nonexistent children and siblings to be 0.
is not smaller in size than the child nodes of its sibling. Clearly, we should consider the sizes of nonexistent children and siblings to be 0.
Consider the following example where  is the node in question,
is the node in question, 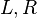 are its child nodes, and
are its child nodes, and 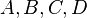 are subtrees which also satisfy the above SBT properties on their own.
are subtrees which also satisfy the above SBT properties on their own.
T
/ \
/ \
L R
/ \ / \
A B C D
Then, the node  must satisfy:
must satisfy:
Rotations
The rotations of SBTs are analogous to those in other self-balancing binary search trees.
------------- Right Rotation ------------
| Q | ---------------> | P |
| / \ | | / \ |
-- P C | | A Q --
/ \ <--- Left Rotation ---> / \
A B <--------------- B C
Left Rotation
left-rotate(t):
k ← t.right
t.right ← k.left
k.left ← t
k.size ← t.size
t.size ← t.left.size + t.right.size + 1
t ← k
Right Rotation
right-rotate(t):
k ← t.left
t.left ← k.right
k.right ← t
k.size ← t.size
t.size ← t.left.size + t.right.size + 1
t ← k
Maintenance
After insertions and deletions, the new sizes of subtrees may violate the two properties above. Thus, we define a procedure maintain(T) to rebalance the SBT rooted at the node  . This should be called with the precondition that
. This should be called with the precondition that  's children are already SBTs themselves. Since property 1 and 2 are symmetrical, we will only discuss property 1.
's children are already SBTs themselves. Since property 1 and 2 are symmetrical, we will only discuss property 1.
There are 4 cases to consider when rebalancing.
- Case 1:
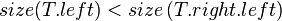
- Perhaps after inserting a value to
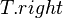 , the scenario below (figure 1) may occur, leading to
, the scenario below (figure 1) may occur, leading to 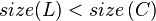 .
. - To fix this, we first perform a
right-rotateon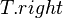 (figure 2) and then a
(figure 2) and then a left-rotateon (figure 3).
(figure 3).
Fig. 1: Fig. 2: Fig. 3:
insert(R,v) right-rotate(R) left-rotate(T)
T T C
/ \ / \ / \
/ \ / \ / \
L R L C T R
/ \ / \ / \ / \ / \ / \
A B C D A B E R L E F D
/ \ / \ / \
E F F D A B
- After these operations, the properties of the entire tree in figure 3 becomes unpredictable. Luckily, the subtrees
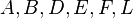 are still SBTs. Thus, we can recursively call
are still SBTs. Thus, we can recursively call maintainon subtrees and
and  to take care of them.
to take care of them. - Now that all of the subtrees are SBTs, we still have to make sure that the root node
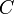 satisfies the SBT properties. So, we call
satisfies the SBT properties. So, we call maintainone last time on root node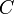 .
.
- Case 2:
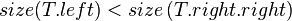
- Perhaps after inserting a value to
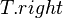 , the scenario below (figure 4) may occur, leading to
, the scenario below (figure 4) may occur, leading to 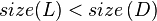 . This is similar to case 1, except that instead of going below
. This is similar to case 1, except that instead of going below 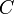 ,
, 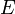 and
and 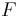 instead goes below
instead goes below 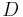 . We can omit them from the diagram.
. We can omit them from the diagram. - Fixing this, we will perform a
left-rotateon the root node , obtaining the structure in figure 5.
, obtaining the structure in figure 5.
Fig. 4: Fig. 5:
insert(R,v) left-rotate(T)
T R
/ \ / \
/ \ / \
L R T D
/ \ / \ / \
A B C D L C
/ \
A B
- After this, the tree rooted at R is still not yet a SBT because
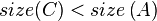 or
or 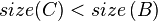 may be true. So, we continue to call
may be true. So, we continue to call maintainon .
. - Now that we have satisfied the precondition of making
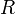 's subtrees SBTs, we may call
's subtrees SBTs, we may call maintainon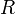 itself.
itself.
- Case 3:
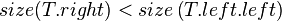
- Symmetrical to case 2.
- Case 4:
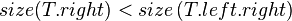
- Symmetrical to case 1.