Shortest path
The shortest paths problem is one of the most fundamental problems in graph theory. Given a directed graph 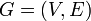 , possibly weighted, and a set of pairs of vertices
, possibly weighted, and a set of pairs of vertices 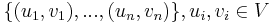 , the problem is to compute, for each
, the problem is to compute, for each  , a path in
, a path in  from
from 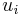 to
to 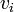 (a list of vertices
(a list of vertices 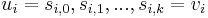 such that for all
such that for all 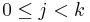 ,
, 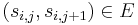 ) such that no other path in
) such that no other path in 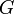 from
from 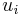 to
to 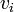 has a lower total weight.
has a lower total weight.
Shortest paths in undirected graphs can be computed by replacing each undirected edge with two arcs of the same weight, one going in each direction, to obtain a directed graph.
Contents
Variations
Three variations of the shortest path algorithm exist, and they are discussed in the following sections.
- In the single-pair shortest path problem, there is only one pair
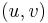 in the problem set. In other words the shortest path is desired between a single pair of vertices.
in the problem set. In other words the shortest path is desired between a single pair of vertices. - In the single-source shortest paths problem, the problem set is of the form
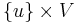 . One vertex,
. One vertex,  , is designated the source, and we wish to find the shortest paths from the source to all other vertices. (To solve the analogous single-destination shortest paths problem, we merely reverse the directions of all edges, which reduces it to single-source.)
, is designated the source, and we wish to find the shortest paths from the source to all other vertices. (To solve the analogous single-destination shortest paths problem, we merely reverse the directions of all edges, which reduces it to single-source.) - In the all-pairs shortest paths problem, the problem set is
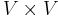 ; that is, we wish to know the shortest paths from every vertex to every other vertex.
; that is, we wish to know the shortest paths from every vertex to every other vertex.
Approach
All the shortest paths algorithms discussed in this article have the same basic approach. At their core, they compute not the shortest paths themselves, but the distances. Using information computed in order to compute the distances, one can easily then reconstruct the paths themselves. They begin with the knowledge that the distance from any vertex to itself is zero, and they overestimate all other distances they need. (By this it is meant that they find a number 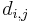 for each pair
for each pair 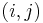 under consideration such that the distance from
under consideration such that the distance from 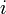 to
to 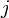 is less than or equal to
is less than or equal to 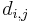 .) At some point, all overestimates will be refined, perhaps gradually, perhaps at once, so that once the algorithm has terminated, they are exactly the correct distances.
.) At some point, all overestimates will be refined, perhaps gradually, perhaps at once, so that once the algorithm has terminated, they are exactly the correct distances.
Relaxation
There are theoretically many ways to refine overestimates but a specific way, known as relaxation, is used in all the algorithms discussed in this article. Relaxation can take place when three conditions are met:
- The currently best overestimate for the distance from some vertex
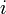 to some vertex
to some vertex 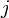 is
is 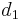 ;
; - The currently best overestimate for the distance from
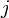 to some vertex
to some vertex 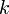 is
is 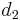 ;
; - The currently best overestimate for the distance from
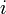 to
to 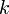 is greater than
is greater than 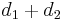 . (This includes the case in which it is infinite.)
. (This includes the case in which it is infinite.)
Relaxation refines the best overestimate for the distance from 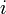 to
to 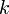 by setting it to
by setting it to 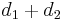 , which is better than its current value.
, which is better than its current value.