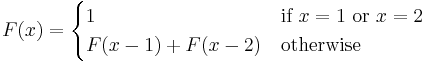Recursive function
Recursion is the property exhibited by entities that are defined in terms of themselves, that is, recur in themselves. In computer science, the most important recursive entities are recursively defined functions. Mathematical functions are usually thought of as sets of ordered pairs, the first element in the pair from the domain, the second from the range, and, hence, a function cannot be intrinsically recursive. However, functions in computer programs are instead defined in a form that allows computers to evaluate them (efficiently, it is hoped), and the definition of a function in a computer program may reference the function itself. Such a function, that occurs in its own definition, is said to be recursively defined, and, with the understanding that we are speaking of the definition of a function rather than its abstract mathematical essence, we will refer to them simply as recursive functions. The term recursion is then defined also as the process of evaluating recursive functions, and, by extension, the formulation of algorithms in terms of recursive functions.
Example
Let 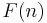 denote the
denote the 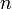 th Fibonacci number, where
th Fibonacci number, where 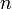 is a natural number and
is a natural number and 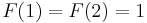 . We may define
. We may define 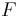 as a function, as follows:
as a function, as follows: