Difference between revisions of "Prefix sum array and difference array"
(a word on the dynamic case) |
m (Reverted edits by 172.69.62.186 (talk) to last revision by 196.221.135.113) |
||
| (6 intermediate revisions by 3 users not shown) | |||
| Line 67: | Line 67: | ||
To solve this, we will first transform array <math>S</math> into its prefix sum array <math>P(0,S)</math>. Notice that the sum of each contiguous subsequence <math>S_i + S_{i+1} + S_{i+2} + ... + S_{j-1}</math> corresponds to the difference of two elements of <math>P</math>, that is, <math>P_j - P_i</math>. So what we want to find is the number of pairs <math>(i,j)</math> with <math>P_j - P_i = 47</math> and <math>i < j</math>. (Note that if <math>i > j</math>, we will instead get a subsequence with sum -47.) | To solve this, we will first transform array <math>S</math> into its prefix sum array <math>P(0,S)</math>. Notice that the sum of each contiguous subsequence <math>S_i + S_{i+1} + S_{i+2} + ... + S_{j-1}</math> corresponds to the difference of two elements of <math>P</math>, that is, <math>P_j - P_i</math>. So what we want to find is the number of pairs <math>(i,j)</math> with <math>P_j - P_i = 47</math> and <math>i < j</math>. (Note that if <math>i > j</math>, we will instead get a subsequence with sum -47.) | ||
| − | However, this is quite easy to do. We sweep through <math>P</math> from left to right, keeping a [[map]] of all elements of <math>P</math> we've seen so far, along with their frequencies; and for each element <math>P_j</math> we count the number of times <math>P_j - | + | However, this is quite easy to do. We sweep through <math>P</math> from left to right, keeping a [[map]] of all elements of <math>P</math> we've seen so far, along with their frequencies; and for each element <math>P_j</math> we count the number of times <math>P_j - 47</math> has appeared so far, by looking up that value in our map; this tells us how many contiguous subsequences ending at <math>S_{j-1}</math> have sum 47. And finally, adding the number of contiguous subsequences with sum 47 ending at each entry of <math>S</math> gives the total number of such subsequences in the array. Total time taken is <math>O(N)</math>, if we use a [[hash table]] implementation of the map. |
==Use of difference array== | ==Use of difference array== | ||
| − | The difference array is used to keep track of an array when ranges of said array can be updated all at once. If we have array <math>A</math> and add an increment <math>k</math> to elements <math>A_i, A_{i+1}, ..., A_{j-1}</math>, then notice that <math>D_0, D_1, ..., D_{i-2}</math> are not affected; that <math>D_{i-1} = A_i - | + | The difference array is used to keep track of an array when ranges of said array can be updated all at once. If we have array <math>A</math> and add an increment <math>k</math> to elements <math>A_i, A_{i+1}, ..., A_{j-1}</math>, then notice that <math>D_0, D_1, ..., D_{i-2}</math> are not affected; that <math>D_{i-1} = A_i - A_{i-1}</math> is increased by <math>k</math>; that <math>D_i, D_{i+1}, ..., D_{j-2}</math> are not affected; that <math>D_{j-1} = A_j - A_{j-1}</math> is decreased by <math>k</math>; and that <math>D_j, D_{j+1}, ...</math> are unaffected. Thus, if we are required to update many ranges of an array in this manner, we should keep track of <math>D</math> rather than <math>A</math> itself, and then integrate at the end to reconstruct <math>A</math>. |
===Example: Wireless (CCC)=== | ===Example: Wireless (CCC)=== | ||
| Line 110: | Line 110: | ||
After the prefix sum array has been computed, we can use it to add together any rectangle in <math>A</math>, that is, all the elements with their indices in <math>[x_1,x_2), [y_1,y_2)</math>. To do so, we first observe that <math>P_{x_2,y_2} - P_{x_1,y_2}</math> gives the sum of all the elements with indices in the box <math>[x_1, x_2) \times [0, y_2)</math>. Then we similarly observe that <math>P_{x_2,y_1} - P_{x_1,y_1}</math> corresponds to the box <math>[x_1, x_2) \times [0, y_1)</math>. Subtracting gives the box <math>[x_1, x_2) \times [y_1, y_2)</math>. This gives a final formula of <math>P_{x_2,y_2} - P_{x_1,y_2} - P_{x_2,y_1} + P_{x_1,y_1}</math>. | After the prefix sum array has been computed, we can use it to add together any rectangle in <math>A</math>, that is, all the elements with their indices in <math>[x_1,x_2), [y_1,y_2)</math>. To do so, we first observe that <math>P_{x_2,y_2} - P_{x_1,y_2}</math> gives the sum of all the elements with indices in the box <math>[x_1, x_2) \times [0, y_2)</math>. Then we similarly observe that <math>P_{x_2,y_1} - P_{x_1,y_1}</math> corresponds to the box <math>[x_1, x_2) \times [0, y_1)</math>. Subtracting gives the box <math>[x_1, x_2) \times [y_1, y_2)</math>. This gives a final formula of <math>P_{x_2,y_2} - P_{x_1,y_2} - P_{x_2,y_1} + P_{x_1,y_1}</math>. | ||
| − | In the <math>n</math>-dimensional case, to sum the elements of <math>A</math> with indices in the box <math>[x_{1,0}, x_{1,1}) \times [x_{2,0}, x_{2,1}) \times ... \times [x_{n,0}, x_{n,1})</math>, we will use the formula <math> | + | In the <math>n</math>-dimensional case, to sum the elements of <math>A</math> with indices in the box <math>[x_{1,0}, x_{1,1}) \times [x_{2,0}, x_{2,1}) \times ... \times [x_{n,0}, x_{n,1})</math>, we will use the formula <math>\sum_{k_1=0}^1 \sum_{k_2=0}^1 ... \sum_{k_n=0}^1 (-1)^{n - k_1 - k_2 - ... - k_n} P_{x_{1,k_1}, x_{2,k_2}, ..., x_{n,k_n}}</math>. We will not state the proof, instead noting that it is a form of the inclusion–exclusion principle. |
====Example: Diamonds (BOI)==== | ====Example: Diamonds (BOI)==== | ||
| Line 119: | Line 119: | ||
We will simply define the difference array <math>D</math> to be the array whose prefix sum array is <math>A</math>. This means in particular that <math>D_{i,j}</math> is the sum of elements of <math>D</math> with indices in the box <math>[i,i+1) \times [j,j+1)</math> (this box contains only the single element <math>D_{i,j}</math>). Using the prefix sum array <math>A</math>, we obtain <math>D_{i,j} = A_{i+1,j+1} - A_{i,j+1} - A_{i+1,j} + A_{i,j}</math>. In general: | We will simply define the difference array <math>D</math> to be the array whose prefix sum array is <math>A</math>. This means in particular that <math>D_{i,j}</math> is the sum of elements of <math>D</math> with indices in the box <math>[i,i+1) \times [j,j+1)</math> (this box contains only the single element <math>D_{i,j}</math>). Using the prefix sum array <math>A</math>, we obtain <math>D_{i,j} = A_{i+1,j+1} - A_{i,j+1} - A_{i+1,j} + A_{i,j}</math>. In general: | ||
| − | :<math>D_{i_1, i_2, ..., i_n} = | + | :<math>D_{i_1, i_2, ..., i_n} = \sum_{k_1=0}^1 \sum_{k_2=0}^1 ... \sum_{k_n=0}^1 (-1)^{n - k_1 - k_2 - ... - k_n} A_{i_1+k_1,i_2+k_2,...,i_n+k_n}</math>. |
Should we actually need to ''compute'' the difference array, on the other hand, the easiest way to do so is by reversing the computation of the prefix sum array: | Should we actually need to ''compute'' the difference array, on the other hand, the easiest way to do so is by reversing the computation of the prefix sum array: | ||
| Line 145: | Line 145: | ||
====Example: The Cake is a Dessert==== | ====Example: The Cake is a Dessert==== | ||
| − | {{Problem|cake|The Cake is a Dessert}} from the | + | {{Problem|cake|The Cake is a Dessert}} from the Waterloo–Woburn 2011 Mock CCC is a straightforward application of the difference array in two dimensions. |
==A word on the dynamic case== | ==A word on the dynamic case== | ||
| − | The dynamic version of the problem that the prefix sum array is intended to solve requires us to be able to carry out an intermixed sequence of operations, where each operation either changes an element of <math>A</math> or asks us to determine the sum <math>A_0 + A_1 + ... + A_{i-1}</math> for some <math>i</math>. That is, we need to be able to compute entries of the prefix sum array of an array that is changing (dynamic). If we can do this, then we can do range sum queries easily on a dynamic array, simply by taking the difference of prefix sums as in the static case. This is a bit trickier to do, but is most easily and efficiently accomplished using the [[binary indexed tree]] data structure, which | + | The dynamic version of the problem that the prefix sum array is intended to solve requires us to be able to carry out an intermixed sequence of operations, where each operation either changes an element of <math>A</math> or asks us to determine the sum <math>A_0 + A_1 + ... + A_{i-1}</math> for some <math>i</math>. That is, we need to be able to compute entries of the prefix sum array of an array that is changing (dynamic). If we can do this, then we can do range sum queries easily on a dynamic array, simply by taking the difference of prefix sums as in the static case. This is a bit trickier to do, but is most easily and efficiently accomplished using the [[binary indexed tree]] data structure, which is specifically designed to solve this problem and can be updated in <math>O(\log(m_1) \log(m_2) ... \log(m_n))</math> time, where <math>n</math> is the number of dimensions and each <math>m</math> is a dimension. Each prefix sum query also takes that amount of time, but we need to perform <math>2^n</math> of these to find a box sum using the formula given previously, so the running time of the query is asymptotically <math>2^n</math> times greater than that of the update. In the most commonly encountered one-dimensional case, both query and update are simply <math>O(\log m)</math>. |
| − | The dynamic version of the problem that the difference array is intended to solve is analogous: we want to be able to increment entire ranges of an array, but at any point we also want to be able to determine any element of the array. Here, we simply use a binary indexed tree for the difference array, and compute prefix sums whenever we want to access an element. | + | The dynamic version of the problem that the difference array is intended to solve is analogous: we want to be able to increment entire ranges of an array, but at any point we also want to be able to determine any element of the array. Here, we simply use a binary indexed tree for the difference array, and compute prefix sums whenever we want to access an element. Here, it is the update that is slower by a factor of <math>2^n</math> than the query (because we have to update <math>2^n</math> entries at a time, but only query one.) |
| − | On the other hand, if we combine the two, that is, we wish to be able to increment ranges of some array <math>A</math> as well as query prefix sums of <math>A</math> in an intermixed sequence, matters become more complicated. Notice that in the static case we would just track the difference array of <math>A</math> and then integrate twice at the end. In the dynamic case, however, we need to use a [[segment tree]] with lazy propagation. This will give us <math>O(2^n \log(m_1) \log(m_2) ... \log(m_n))</math> time on both the query and the update, but is somewhat more complex and slower than the binary indexed tree. | + | On the other hand, if we combine the two, that is, we wish to be able to increment ranges of some array <math>A</math> as well as query prefix sums of <math>A</math> in an intermixed sequence, matters become more complicated. Notice that in the static case we would just track the difference array of <math>A</math> and then integrate twice at the end. In the dynamic case, however, we need to use a [[segment tree]] with lazy propagation. This will give us <math>O(2^n \log(m_1) \log(m_2) ... \log(m_n))</math> time on both the query and the update, but is somewhat more complex and slower than the binary indexed tree on the [[invisible constant factor]]. |
[[Category:Pages needing diagrams]] | [[Category:Pages needing diagrams]] | ||
Revision as of 22:16, 26 March 2018
Given an array of numbers, we can construct a new array by replacing each element by the difference between itself and the previous element, except for the first element, which we simply ignore. This is called the difference array, because it contains the first differences of the original array. We will denote the difference array of array  by
by 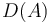 . For example, the difference array of
. For example, the difference array of ![A = [9, 2, 6, 3, 1, 5, 0, 7]](/wiki/images/math/7/f/9/7f9d88c652b184dc4db1a19714f6dd80.png) is
is ![D(A) = [2-9, 6-2, 3-6, 1-3, 5-1, 0-5, 7-0]](/wiki/images/math/e/3/5/e35ce6a5ac5351ad3daf63f72445d05b.png) , or
, or ![[-7, 4, -3, -2, 4, -5, 7]](/wiki/images/math/a/d/d/add580769fa99a870317b923383072b7.png) .
.
We see that the difference array can be computed in linear time from the original array, and is shorter than the original array by one element. Here are implementations in C and Haskell. (Note that the Haskell implementation actually takes a list, but returns an array.)
// D must have enough space for n-1 ints void difference_array(int* A, int n, int* D) { for (int i = 0; i < n-1; i++) D[i] = A[i+1] - A[i]; }
d :: [Int] -> Array Int [Int] d a = listArray (0, length a - 2) (zipWith (-) (tail a) a)
The prefix sum array is the opposite of the difference array. Given an array of numbers  and an arbitrary constant
and an arbitrary constant  , we first append
, we first append  onto the front of the array, and then replace each element with the sum of itself and all the elements preceding it. For example, if we start with
onto the front of the array, and then replace each element with the sum of itself and all the elements preceding it. For example, if we start with ![A = [9, 2, 6, 3, 1, 5, 0, 7]](/wiki/images/math/7/f/9/7f9d88c652b184dc4db1a19714f6dd80.png) , and choose to append the arbitrary value
, and choose to append the arbitrary value 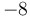 to the front, we obtain
to the front, we obtain ![P(-8, A) = [-8, -8+9, -8+9+2, -8+9+2+6, ..., -8+9+2+6+3+1+5+0+7]](/wiki/images/math/3/0/a/30a6494f688a01d72adad9f368016095.png) , or
, or ![[-8, 1, 3, 9, 12, 13, 18, 18, 25]](/wiki/images/math/5/c/c/5cc1dad3f6d3c0ccea7d7d3dd92c5bc8.png) . Computing the prefix sum array can be done in linear time as well, and the prefix sum array is longer than the original array by one element:
. Computing the prefix sum array can be done in linear time as well, and the prefix sum array is longer than the original array by one element:
// P must have enough space for n+1 ints void prefix_sum_array(int c, int* A, int n, int* P) { P[0] = c; for (int i = 0; i < n; i++) P[i+1] = P[i] + A[i]; }
p :: Int -> [Int] -> Array Int [Int] p c a = listArray (0, length a) (scanl (+) c a)
Note that every array has an infinite number of possible prefix sum arrays, since we can choose whatever value we want for  . For convenience, we usually choose
. For convenience, we usually choose 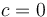 . However, changing the value of
. However, changing the value of  has only the effect of shifting all the elements of
has only the effect of shifting all the elements of 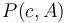 by a constant. For example,
by a constant. For example, ![P(15, A) = [15, 24, 26, 32, 35, 36, 41, 41, 48]](/wiki/images/math/2/f/5/2f55d6c3a47d61dae3b77320f34e8d9d.png) . However, each element of
. However, each element of 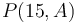 is exactly 23 more than the corresponding element from
is exactly 23 more than the corresponding element from 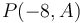 .
.
The functions 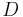 and
and  carry out reverse processes. Given an nonempty zero-indexed array
carry out reverse processes. Given an nonempty zero-indexed array  :
:
-
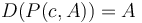 for any
for any  . For example, taking the difference array of
. For example, taking the difference array of ![P(-8, A) = [-8, 1, 3, 9, 12, 13, 18, 18, 25]](/wiki/images/math/0/2/b/02b6898dffbc07ad061a917cb0a015c4.png) gives
gives ![[9, 2, 6, 3, 1, 5, 0, 7]](/wiki/images/math/a/3/e/a3e4109270a19cac82c7e91bec7564e4.png) , that is, it restores the original array
, that is, it restores the original array  .
. -
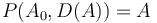 . Thus, taking
. Thus, taking ![D(A) = [-7, 4, -3, -2, 4, -5, 7]](/wiki/images/math/f/4/4/f4480db6ad3c47e96c7874fcfcea1336.png) and
and 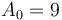 (initial element of
(initial element of  ), we have
), we have ![P(A_0, D(A)) = [9, 2, 6, 3, 1, 5, 0, 7]](/wiki/images/math/9/7/a/97a41ef3e4d9b2e3dde402ac06122ea8.png) , again restoring the original array
, again restoring the original array  .
.
Contents
Analogy with calculus
These two processes—computing the difference array, and computing a prefix sum array—are the discrete equivalents of differentiation and integration in calculus, which operate on continuous domains. An entry in an array is like the value of a function at a particular point.
- Reverse processes:
-
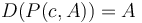 for any
for any  . Likewise
. Likewise 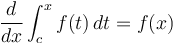 for any
for any  .
. -
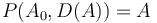 . Likewise
. Likewise 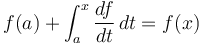 .
.
-
- Uniqueness:
- A differentiable function
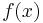 can only have one derivative,
can only have one derivative, 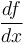 . An array
. An array  can only have one difference array,
can only have one difference array, 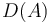 .
. - A continuous function
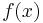 has an infinite number of antiderivatives,
has an infinite number of antiderivatives, 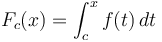 , where
, where  can be any number in its domain, but they differ only by a constant (their graphs are vertical translations of each other). An array
can be any number in its domain, but they differ only by a constant (their graphs are vertical translations of each other). An array  has an infinite number of prefix arrays
has an infinite number of prefix arrays 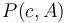 , but they differ only by a constant (at each entry).
, but they differ only by a constant (at each entry).
- A differentiable function
- Given some function
![f:[a,b]\to\mathbb{R}](/wiki/images/math/3/3/2/332d0f0f6103ad3c4ec22d3af5b36e7c.png) , and the fact that
, and the fact that 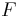 , an antiderivative of
, an antiderivative of  , satisfies
, satisfies 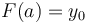 , we can uniquely reconstruct
, we can uniquely reconstruct 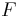 . That is, even though
. That is, even though  has an infinite number of antiderivatives, we can pin it down to one once we are given the value the antiderivative is supposed to attain on the left edge of
has an infinite number of antiderivatives, we can pin it down to one once we are given the value the antiderivative is supposed to attain on the left edge of  's domain. Likewise, given some array
's domain. Likewise, given some array  and the fact that
and the fact that  , a prefix sum array of
, a prefix sum array of  , satisfies
, satisfies 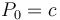 , we can uniquely reconstruct
, we can uniquely reconstruct  .
. - Effect on length:
-
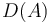 is shorter than
is shorter than  by one element. Differentiating
by one element. Differentiating ![f:[a,b] \to \mathbb{R}](/wiki/images/math/3/3/2/332d0f0f6103ad3c4ec22d3af5b36e7c.png) gives a function
gives a function 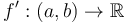 (shortens the closed interval to an open interval).
(shortens the closed interval to an open interval). -
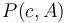 is longer than
is longer than  by one element. Integrating
by one element. Integrating 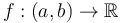 gives a function
gives a function ![F:[a,b] \to \mathbb{R}](/wiki/images/math/1/9/b/19b17cac5b2437be7e4aa88212b6ddc4.png) (lengthens the open interval to a closed interval).
(lengthens the open interval to a closed interval).
-
Because of these similarities, we will speak simply of differentiating and integrating arrays. An array can be differentiated multiple times, but eventually it will shrink to length 0. An array can be integrated any number of times.
Use of prefix sum array
The Fundamental Theorem of Calculus also has an analogue, which is why the prefix sum array is so useful. To compute an integral 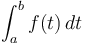 , which is like a continuous kind of sum of an infinite number of function values
, which is like a continuous kind of sum of an infinite number of function values 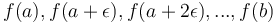 , we take any antiderivative
, we take any antiderivative 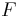 , and compute
, and compute  . Likewise, to compute the sum of values
. Likewise, to compute the sum of values 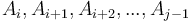 , we will take any prefix array
, we will take any prefix array 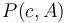 and compute
and compute  . Notice that just as we can use any antiderivative
. Notice that just as we can use any antiderivative 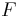 because the constant cancels out, we can use any prefix sum array because the initial value cancels out. (Note our use of the left half-open interval.)
because the constant cancels out, we can use any prefix sum array because the initial value cancels out. (Note our use of the left half-open interval.)
Proof: 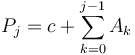 and
and 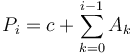 . Subtracting gives
. Subtracting gives 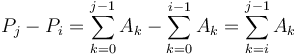 as desired.
as desired. 
This is best illustrated via example. Let ![A = [9,2,6,3,1,5,0,7]](/wiki/images/math/7/f/9/7f9d88c652b184dc4db1a19714f6dd80.png) as before. Take
as before. Take ![P(0,A) = [0, 9, 11, 17, 20, 21, 26, 26, 33]](/wiki/images/math/c/4/7/c473217b3594e5fed86c3fbef7cc3894.png) . Then, suppose we want
. Then, suppose we want 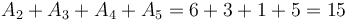 . We can compute this by taking
. We can compute this by taking 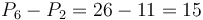 . This is because
. This is because 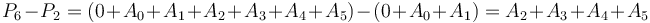 .
.
When we use the prefix sum array in this case, we generally use 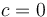 for convenience (although we are theoretically free to use any value we wish), and speak of the prefix sum array obtained this way as simply the prefix sum array.
for convenience (although we are theoretically free to use any value we wish), and speak of the prefix sum array obtained this way as simply the prefix sum array.
Example: Counting Subsequences (SPOJ)
Computing the prefix sum array is rarely the most difficult part of a problem. Instead, the prefix sum array is kept on hand because the algorithm to solve the problem makes frequent reference to range sums.
We will consider the problem Counting Subsequences from IPSC 2006. Here we are given an array of integers  and asked to find the number of contiguous subsequences of the array that sum to 47.
and asked to find the number of contiguous subsequences of the array that sum to 47.
To solve this, we will first transform array  into its prefix sum array
into its prefix sum array 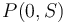 . Notice that the sum of each contiguous subsequence
. Notice that the sum of each contiguous subsequence 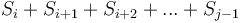 corresponds to the difference of two elements of
corresponds to the difference of two elements of  , that is,
, that is,  . So what we want to find is the number of pairs
. So what we want to find is the number of pairs 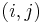 with
with 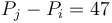 and
and 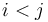 . (Note that if
. (Note that if 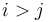 , we will instead get a subsequence with sum -47.)
, we will instead get a subsequence with sum -47.)
However, this is quite easy to do. We sweep through  from left to right, keeping a map of all elements of
from left to right, keeping a map of all elements of  we've seen so far, along with their frequencies; and for each element
we've seen so far, along with their frequencies; and for each element 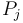 we count the number of times
we count the number of times  has appeared so far, by looking up that value in our map; this tells us how many contiguous subsequences ending at
has appeared so far, by looking up that value in our map; this tells us how many contiguous subsequences ending at 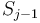 have sum 47. And finally, adding the number of contiguous subsequences with sum 47 ending at each entry of
have sum 47. And finally, adding the number of contiguous subsequences with sum 47 ending at each entry of  gives the total number of such subsequences in the array. Total time taken is
gives the total number of such subsequences in the array. Total time taken is  , if we use a hash table implementation of the map.
, if we use a hash table implementation of the map.
Use of difference array
The difference array is used to keep track of an array when ranges of said array can be updated all at once. If we have array  and add an increment
and add an increment  to elements
to elements 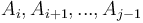 , then notice that
, then notice that 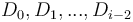 are not affected; that
are not affected; that 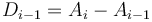 is increased by
is increased by  ; that
; that 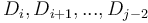 are not affected; that
are not affected; that 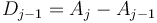 is decreased by
is decreased by  ; and that
; and that 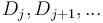 are unaffected. Thus, if we are required to update many ranges of an array in this manner, we should keep track of
are unaffected. Thus, if we are required to update many ranges of an array in this manner, we should keep track of 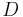 rather than
rather than  itself, and then integrate at the end to reconstruct
itself, and then integrate at the end to reconstruct  .
.
Example: Wireless (CCC)
This is the basis of the model solution to Wireless from CCC 2009. We are given a grid of lattice points with up to 30000 rows and up to 1000 columns, and up to 1000 circles, each of which is centered at a lattice point. Each circle has a particular weight associated with it. We want to stand at a lattice point such that the sum of the weights of all the circles covering it is maximized, and to determine how many such lattice points there are.
The most straightforward way to do this is by actually computing the sum of weights of all covering circles at each individual lattice point. However, doing this naively would take up to 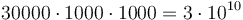 operations, as we would have to consider each lattice point and each circle and decide whether that circle covers that lattice point.
operations, as we would have to consider each lattice point and each circle and decide whether that circle covers that lattice point.
To solve this, we will treat each column of the lattice as an array  , where entry
, where entry 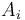 denotes the sum of weights of all the circles covering the point in row
denotes the sum of weights of all the circles covering the point in row  of that column. Now, consider any of the given circles. Either this circle does not cover any points in this column at all, or the points it covers in this column will all be consecutive. (This is equivalent to saying that the intersection of a circle with a line is a line segment.) For example, a circle centered at
of that column. Now, consider any of the given circles. Either this circle does not cover any points in this column at all, or the points it covers in this column will all be consecutive. (This is equivalent to saying that the intersection of a circle with a line is a line segment.) For example, a circle centered at 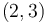 with radius
with radius 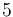 will cover no lattice points with x-coordinate
will cover no lattice points with x-coordinate 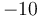 , and as for lattice points with x-coordinate
, and as for lattice points with x-coordinate 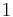 , it will cover
, it will cover 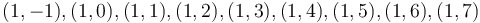 . Thus, the circle covers some first point
. Thus, the circle covers some first point  and some last point
and some last point  , and adds some value
, and adds some value  to each point that it covers; that is, it adds
to each point that it covers; that is, it adds  to
to 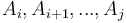 . Thus, we will simply maintain the difference array
. Thus, we will simply maintain the difference array 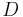 , noting that the circle adds
, noting that the circle adds  to
to 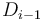 and takes
and takes  away from
away from 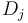 . We maintain such a difference array for each column; and we perform at most two updates for each circle-column pair; so the total number of updates is bounded by
. We maintain such a difference array for each column; and we perform at most two updates for each circle-column pair; so the total number of updates is bounded by 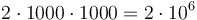 . (The detail of how to keep track of the initial element of
. (The detail of how to keep track of the initial element of  is left as an exercise to the reader.) After this, we perform integration on each column and find the maximum values, which requires at most a constant times the total number of lattice points, which is up to
is left as an exercise to the reader.) After this, we perform integration on each column and find the maximum values, which requires at most a constant times the total number of lattice points, which is up to 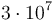 .
.
Multiple dimensions
The prefix sum array and difference array can be extended to multiple dimensions.
Prefix sum array
We start by considering the two-dimensional case. Given an 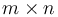 array
array  , we will define the prefix sum array
, we will define the prefix sum array 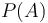 as follows:
as follows: 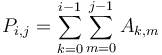 . In other words, the first row of
. In other words, the first row of  is all zeroes, the first column of
is all zeroes, the first column of  is all zeroes, and all other elements of
is all zeroes, and all other elements of  are obtained by adding up some upper-left rectangle of values of
are obtained by adding up some upper-left rectangle of values of  . For example,
. For example, 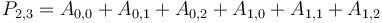 . Or, more easily expressed,
. Or, more easily expressed, 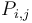 is the sum of all entries of
is the sum of all entries of  with indices in
with indices in 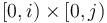 (Cartesian product).
(Cartesian product).
In general, if we are given an  -dimensional array
-dimensional array  with dimensions
with dimensions 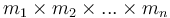 , then the prefix sum array has dimensions
, then the prefix sum array has dimensions 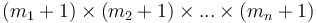 , and is defined by
, and is defined by 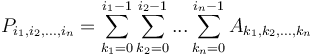 ; or we can simply say that it is the sum of all entries of
; or we can simply say that it is the sum of all entries of  with indices in
with indices in 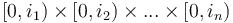 .
.
To compute the prefix sum array in the two-dimensional case, we will scan first down and then right, as suggested by the following C++ implementation:
vector<vector<int> > P(vector<vector<int> > A) { int m = A.size(); int n = A[0].size(); // Make an m+1 by n+1 array and initialize it with zeroes. vector<vector<int> > p(m+1, vector<int>(n+1, 0)); for (int i = 1; i <= m; i++) for (int j = 1; j <= n; j++) p[i][j] = p[i-1][j] + A[i-1][j-1]; for (int i = 1; i <= m; i++) for (int j = 1; j <= n; j++) p[i][j] += p[i][j-1]; return p; }
Here, we first make each column of  the prefix sum array of a column of
the prefix sum array of a column of  , then convert each row of
, then convert each row of  into its prefix sum array to obtain the final values. That is, after the first pair of for loops,
into its prefix sum array to obtain the final values. That is, after the first pair of for loops, 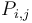 will be equal to
will be equal to 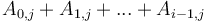 , and after the second pair, we will then have
, and after the second pair, we will then have 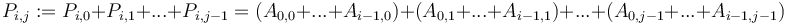 , as desired. The extension of this to more than two dimensions is straightforward.
, as desired. The extension of this to more than two dimensions is straightforward.
(Haskell code is not shown, because using functional programming in this case does not make the code nicer.)
After the prefix sum array has been computed, we can use it to add together any rectangle in  , that is, all the elements with their indices in
, that is, all the elements with their indices in 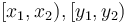 . To do so, we first observe that
. To do so, we first observe that  gives the sum of all the elements with indices in the box
gives the sum of all the elements with indices in the box 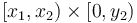 . Then we similarly observe that
. Then we similarly observe that  corresponds to the box
corresponds to the box 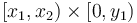 . Subtracting gives the box
. Subtracting gives the box  . This gives a final formula of
. This gives a final formula of  .
.
In the  -dimensional case, to sum the elements of
-dimensional case, to sum the elements of  with indices in the box
with indices in the box 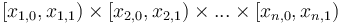 , we will use the formula
, we will use the formula 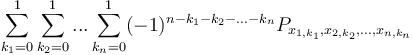 . We will not state the proof, instead noting that it is a form of the inclusion–exclusion principle.
. We will not state the proof, instead noting that it is a form of the inclusion–exclusion principle.
Example: Diamonds (BOI)
The problem Diamonds from BOI '09 is a straightforward application of the prefix sum array in three dimensions. We read in a three-dimensional array  , and then compute its prefix sum array; after doing this, we will be able to determine the sum of any box of the array with indices in the box
, and then compute its prefix sum array; after doing this, we will be able to determine the sum of any box of the array with indices in the box 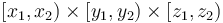 as
as 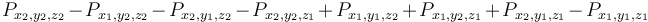 .
.
Difference array
To use the difference array properly in two dimensions, it is easiest to use a source array  with the property that the first row and first column consist entirely of zeroes. (In multiple dimensions, we will want
with the property that the first row and first column consist entirely of zeroes. (In multiple dimensions, we will want 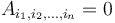 whenever any of the
whenever any of the  's are zero.)
's are zero.)
We will simply define the difference array 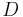 to be the array whose prefix sum array is
to be the array whose prefix sum array is  . This means in particular that
. This means in particular that 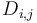 is the sum of elements of
is the sum of elements of 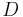 with indices in the box
with indices in the box  (this box contains only the single element
(this box contains only the single element 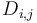 ). Using the prefix sum array
). Using the prefix sum array  , we obtain
, we obtain 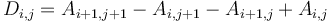 . In general:
. In general:
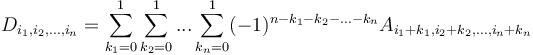 .
.
Should we actually need to compute the difference array, on the other hand, the easiest way to do so is by reversing the computation of the prefix sum array:
vector<vector<int> > D(vector<vector<int> > A) { int m = A.size(); int n = A[0].size(); // Make an m+1 by n+1 array vector<vector<int> > d(m-1, vector<int>(n-1)); for (int i = 0; i < m-1; i++) for (int j = 0; j < n-1; j++) d[i][j] = A[i+1][j+1] - A[i+1][j]; for (int i = m-2; i > 0; i--) for (int j = 0; j < n-1; j++) d[i][j] -= d[i-1][j]; return d; }
In this code, we first make each column of 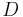 the difference array of the corresponding column of
the difference array of the corresponding column of  , and then treat each row as now being the prefix sum array of the final result (the row of the difference array), so we scan backward through it to reconstruct the original array (i.e., take the difference array of the row). (We have to do this backward so that we won't overwrite a value we still need later.) The extension to multiple dimensions is straightforward; we simply have to walk backward over every additional dimension as well.
, and then treat each row as now being the prefix sum array of the final result (the row of the difference array), so we scan backward through it to reconstruct the original array (i.e., take the difference array of the row). (We have to do this backward so that we won't overwrite a value we still need later.) The extension to multiple dimensions is straightforward; we simply have to walk backward over every additional dimension as well.
Now we consider what happens when all elements of  with coordinates in the box given by
with coordinates in the box given by 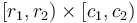 are incremented by
are incremented by  . If we take the difference array of each column of
. If we take the difference array of each column of  now, as in the function
now, as in the function D defined above, we see that for each column, we will have to add  to entry
to entry 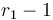 and subtract it from
and subtract it from 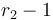 (as in the one-dimensional case). Now if we take the difference array of each row of what we've just obtained, we notice that in row number
(as in the one-dimensional case). Now if we take the difference array of each row of what we've just obtained, we notice that in row number 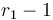 , we've added
, we've added  to every element in columns in
to every element in columns in 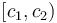 in the previous step, and in row number
in the previous step, and in row number 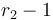 , we've subtracted
, we've subtracted  to every element in the same column range, so in the end the effect is to add
to every element in the same column range, so in the end the effect is to add  to elements
to elements 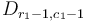 and
and 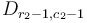 , and to subtract
, and to subtract  from elements
from elements 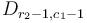 and
and 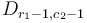 .
.
In the general case, when adding  to all elements of
to all elements of  with indices in the box
with indices in the box 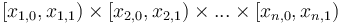 , a total of
, a total of 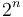 elements of
elements of 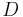 need to be updated. In particular, element
need to be updated. In particular, element 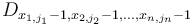 (where each of the
(where each of the  's can be either 0 or 1, giving
's can be either 0 or 1, giving 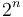 possibilities in total) is incremented by
possibilities in total) is incremented by 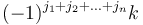 . That is, if we consider an
. That is, if we consider an  -dimensional array to be an
-dimensional array to be an  -dimensional hypercube of numbers, then the elements to be updated lie on the corners of an
-dimensional hypercube of numbers, then the elements to be updated lie on the corners of an  -dimensional hypercube; we 2-color the vertices black and white (meaning two adjacent vertices always have opposite colours), with the lowest corner (corresponding to indices
-dimensional hypercube; we 2-color the vertices black and white (meaning two adjacent vertices always have opposite colours), with the lowest corner (corresponding to indices ![[x_{1,0}-1, x_{2,0}-1, ..., x_{n,0}-1]](/wiki/images/math/e/e/9/ee969b6f137475e7cbacf3b7c020acbb.png) ) white; and each white vertex receiving
) white; and each white vertex receiving 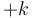 and each black vertex
and each black vertex 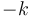 . One can attempt to visualize the effect this has on the prefix sum array in three dimensions, and become convinced that it makes sense in
. One can attempt to visualize the effect this has on the prefix sum array in three dimensions, and become convinced that it makes sense in  dimensions. Each element in the prefix sum array
dimensions. Each element in the prefix sum array 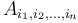 is the sum of all the elements in some box of the difference array with its lowest corner at the origin,
is the sum of all the elements in some box of the difference array with its lowest corner at the origin, 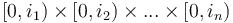 . If the highest corner actually lies within the hypercube, that is,
. If the highest corner actually lies within the hypercube, that is, 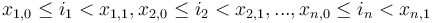 , then this box is only going to contain the low corner
, then this box is only going to contain the low corner 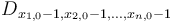 , which has increased by
, which has increased by  ; thus, this entry in
; thus, this entry in  has increased by
has increased by  as well, and this is true of all elements that lie within the hypercube,
as well, and this is true of all elements that lie within the hypercube, 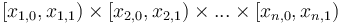 . If any of the
. If any of the  's are less than the lower bound of the corresponding
's are less than the lower bound of the corresponding  , then our box doesn't hit any of the vertices of the hypercube at all, so all these elements are unaffected; and if instead any one of them goes over the upper bound, then our box passes in through one hyperface and out through another, which means that corresponding vertices on the low and high face will either both be hit or both not be hit, and each pair cancels itself out, giving again no change outside the hypercube.
, then our box doesn't hit any of the vertices of the hypercube at all, so all these elements are unaffected; and if instead any one of them goes over the upper bound, then our box passes in through one hyperface and out through another, which means that corresponding vertices on the low and high face will either both be hit or both not be hit, and each pair cancels itself out, giving again no change outside the hypercube.
Example: The Cake is a Dessert
The Cake is a Dessert from the Waterloo–Woburn 2011 Mock CCC is a straightforward application of the difference array in two dimensions.
A word on the dynamic case
The dynamic version of the problem that the prefix sum array is intended to solve requires us to be able to carry out an intermixed sequence of operations, where each operation either changes an element of  or asks us to determine the sum
or asks us to determine the sum 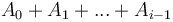 for some
for some  . That is, we need to be able to compute entries of the prefix sum array of an array that is changing (dynamic). If we can do this, then we can do range sum queries easily on a dynamic array, simply by taking the difference of prefix sums as in the static case. This is a bit trickier to do, but is most easily and efficiently accomplished using the binary indexed tree data structure, which is specifically designed to solve this problem and can be updated in
. That is, we need to be able to compute entries of the prefix sum array of an array that is changing (dynamic). If we can do this, then we can do range sum queries easily on a dynamic array, simply by taking the difference of prefix sums as in the static case. This is a bit trickier to do, but is most easily and efficiently accomplished using the binary indexed tree data structure, which is specifically designed to solve this problem and can be updated in 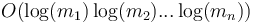 time, where
time, where  is the number of dimensions and each
is the number of dimensions and each 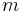 is a dimension. Each prefix sum query also takes that amount of time, but we need to perform
is a dimension. Each prefix sum query also takes that amount of time, but we need to perform 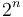 of these to find a box sum using the formula given previously, so the running time of the query is asymptotically
of these to find a box sum using the formula given previously, so the running time of the query is asymptotically 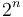 times greater than that of the update. In the most commonly encountered one-dimensional case, both query and update are simply
times greater than that of the update. In the most commonly encountered one-dimensional case, both query and update are simply 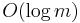 .
.
The dynamic version of the problem that the difference array is intended to solve is analogous: we want to be able to increment entire ranges of an array, but at any point we also want to be able to determine any element of the array. Here, we simply use a binary indexed tree for the difference array, and compute prefix sums whenever we want to access an element. Here, it is the update that is slower by a factor of 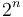 than the query (because we have to update
than the query (because we have to update 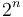 entries at a time, but only query one.)
entries at a time, but only query one.)
On the other hand, if we combine the two, that is, we wish to be able to increment ranges of some array  as well as query prefix sums of
as well as query prefix sums of  in an intermixed sequence, matters become more complicated. Notice that in the static case we would just track the difference array of
in an intermixed sequence, matters become more complicated. Notice that in the static case we would just track the difference array of  and then integrate twice at the end. In the dynamic case, however, we need to use a segment tree with lazy propagation. This will give us
and then integrate twice at the end. In the dynamic case, however, we need to use a segment tree with lazy propagation. This will give us 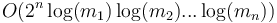 time on both the query and the update, but is somewhat more complex and slower than the binary indexed tree on the invisible constant factor.
time on both the query and the update, but is somewhat more complex and slower than the binary indexed tree on the invisible constant factor.