Difference between revisions of "Prefix sum array and difference array"
(easier example problem) |
(rewrite --- should be easier to read now) |
||
| Line 1: | Line 1: | ||
| − | Given an [[array]] of numbers, we can construct a new array by replacing each element by the difference between itself and the previous element, except for the first element, which we simply ignore. This is called the '''difference array''', because it contains the first differences of the original array. For example, the difference array of <math>A = [9, 2, 6, 3, 1, 5, 0, 7]</math> is <math>D = [2-9, 6-2, 3-6, 1-3, 5-1, 0-5, 7-0]</math>, or <math>[-7, 4, -3, -2, 4, -5, 7]</math> | + | Given an [[array]] of numbers, we can construct a new array by replacing each element by the difference between itself and the previous element, except for the first element, which we simply ignore. This is called the '''difference array''', because it contains the first differences of the original array. We will denote the difference array of array <math>A</math> by <math>D(A)</math>. For example, the difference array of <math>A = [9, 2, 6, 3, 1, 5, 0, 7]</math> is <math>D(A) = [2-9, 6-2, 3-6, 1-3, 5-1, 0-5, 7-0]</math>, or <math>[-7, 4, -3, -2, 4, -5, 7]</math>. |
| − | We can | + | We see that the difference array can be computed in [[linear time]] from the original array, and is shorter than the original array by one element. Here are implementations in C and Haskell. (Note that the Haskell implementation actually takes a list, not an array, and will work fine for infinite lists.) |
| + | <syntaxhighlight lang="c"> | ||
| + | // D must have enough space for n-1 ints | ||
| + | void difference_array(int* A, int n, int* D) | ||
| + | { | ||
| + | for (int i = 0; i < n-1; i++) | ||
| + | D[i] = A[i+1] - A[i]; | ||
| + | } | ||
| + | </syntaxhighlight><br/> | ||
| + | <syntaxhighlight lang="haskell"> | ||
| + | d :: [Int] -> [Int] -- NB: The general type signature should be (Num a) => [a] -> [a] | ||
| + | d a = zipWith (-) (tail a) a | ||
| + | </syntaxhighlight><br/> | ||
| + | |||
| + | The '''prefix sum array''' is the opposite of the difference array. Given an array of numbers <math>A</math> and an arbitrary constant <math>c</math>, we first append <math>c</math> onto the front of the array, and then replace each element with the sum of itself and all the elements preceding it. For example, if we start with <math>A = [9, 2, 6, 3, 1, 5, 0, 7]</math>, and choose to append the arbitrary value <math>-8</math> to the front, we obtain <math>P(-8, A) = [-8, -8+9, -8+9+2, -8+9+2+6, ..., -8+9+2+6+3+1+5+0+7]</math>, or <math>[-8, 1, 3, 9, 12, 13, 18, 18, 25]</math>. Computing the prefix sum array can be done in linear time as well, and the prefix sum array is longer than the original array by one element: | ||
| + | <syntaxhighlight lang="c"> | ||
| + | // P must have enough space for n+1 ints | ||
| + | void prefix_sum_array(int c, int* A, int n, int* P) | ||
| + | { | ||
| + | P[0] = c; | ||
| + | for (int i = 0; i < n; i++) | ||
| + | P[i+1] = P[i] + A[i]; | ||
| + | } | ||
| + | </syntaxhighlight><br/> | ||
| + | <syntaxhighlight lang="haskell"> | ||
| + | p :: Int -> [Int] -> [Int] -- NB: The general type signature should be (Num a) => a -> [a] -> [a] | ||
| + | p = scanl (+) -- NB: This is the same as p c a = scanl (+) c a | ||
| + | </syntaxhighlight><br/> | ||
| + | |||
| + | Note that every array has an infinite number of possible prefix sum arrays, since we can choose whatever value we want for <math>c</math>. For convenience, we usually choose <math>c = 0</math>. However, changing the value of <math>c</math> has only the effect of shifting all the elements of <math>P(c,A)</math> by a constant. For example, <math>P(15, A) = [15, 24, 26, 32, 35, 36, 41, 41, 48]</math>. However, each element of <math>P(15, A)</math> is exactly 23 more than the corresponding element from <math>P(-8, A)</math>. | ||
| + | |||
| + | The functions <math>D</math> and <math>P</math> carry out '''reverse processes'''. Given an nonempty zero-indexed array <math>A</math>: | ||
| + | # <math>D(P(c, A)) = A</math> for any <math>c</math>. For example, taking the difference array of <math>P(-8, A) = [-8, 1, 3, 9, 12, 13, 18, 18, 25]</math> gives <math>[9, 2, 6, 3, 1, 5, 0, 7]</math>, that is, it restores the original array <math>A</math>. | ||
| + | # <math>P(A_0, D(A)) = A</math>. Thus, taking <math>D(A) = [-7, 4, -3, -2, 4, -5, 7]</math> and <math>A_0 = 9</math> (initial element of <math>A</math>), we have <math>P(A_0, D(A)) = [9, 2, 6, 3, 1, 5, 0, 7]</math>, again restoring the original array <math>A</math>. | ||
==Analogy with calculus== | ==Analogy with calculus== | ||
| − | These two processes—computing the difference array, and computing a prefix sum array—are the discrete equivalents of differentiation and integration in calculus, which operate on continuous domains: | + | These two processes—computing the difference array, and computing a prefix sum array—are the discrete equivalents of differentiation and integration in calculus, which operate on continuous domains. An entry in an array is like the value of a function at a particular point. |
| − | * | + | * ''Reverse processes'': |
| − | * A function can only have one derivative, | + | :* <math>D(P(c, A)) = A</math> for any <math>c</math>. Likewise <math>\frac{d}{dx} \int_c^x f(t)\, dt = f(x)</math> for any <math>c</math>. |
| − | * | + | :* <math>P(A_0, D(A)) = A</math>. Likewise <math>f(a) + \int_a^x \frac{df}{dt}\, dt = f(x)</math>. |
| − | * | + | * ''Uniqueness'': |
| − | + | :* A differentiable function <math>f(x)</math> can only have one derivative, <math>\frac{df}{dx}</math>. An array <math>A</math> can only have one difference array, <math>D(A)</math>. | |
| − | Because of these similarities, we will speak simply of ''differentiating'' and ''integrating'' arrays. An array can be differentiated multiple times, but eventually it will shrink to length 0. An array can be integrated any number of times | + | :* A continuous function <math>f(x)</math> has an infinite number of antiderivatives, <math>F_c(x) = \int_c^x f(t)\, dt</math>, where <math>c</math> can be any number in its domain, but they differ only by a constant (their graphs are vertical translations of each other). An array <math>A</math> has an infinite number of prefix arrays <math>P(c,A)</math>, but they differ only by a constant (at each entry). |
| + | * Given some function <math>f:[a,b]\to\mathbb{R}</math>, and the fact that <math>F</math>, an antiderivative of <math>f</math>, satisfies <math>F(a) = y_0</math>, we can uniquely reconstruct <math>F</math>. That is, even though <math>f</math> has an infinite number of antiderivatives, we can pin it down to one once we are given the value the antiderivative is supposed to attain on the left edge of <math>f</math>'s domain. Likewise, given some array <math>A</math> and the fact that <math>P</math>, a prefix sum array of <math>A</math>, satisfies <math>P_0 = c</math>, we can uniquely reconstruct <math>P</math>. | ||
| + | * ''Effect on length'': | ||
| + | :* <math>D(A)</math> is shorter than <math>A</math> by one element. Differentiating <math>f:[a,b] \to \mathbb{R}</math> gives a function <math>f':(a,b) \to \mathbb{R}</math> (shortens the closed interval to an open interval). | ||
| + | :* <math>P(c,A)</math> is longer than <math>A</math> by one element. Integrating <math>f:(a,b) \to \mathbb{R}</math> gives a function <math>F:[a,b] \to \mathbb{R}</math> (lengthens the open interval to a closed interval). | ||
| + | |||
| + | Because of these similarities, we will speak simply of ''differentiating'' and ''integrating'' arrays. An array can be differentiated multiple times, but eventually it will shrink to length 0. An array can be integrated any number of times. | ||
==Use of prefix sum array== | ==Use of prefix sum array== | ||
| − | The Fundamental Theorem of Calculus also has an analogue, which is why the prefix sum array is so useful. | + | The Fundamental Theorem of Calculus also has an analogue, which is why the prefix sum array is so useful. To compute an integral <math>\int_a^b f(t)\, dt</math>, which is like a continuous kind of sum of an infinite number of function values <math>f(a), f(a+\epsilon), f(a+2\epsilon), ..., f(b)</math>, we take any antiderivative <math>F</math>, and compute <math>F(b) - F(a)</math>. Likewise, to compute the sum of values <math>A_i, A_{i+1}, A_{i+2}, ..., A_{j-1}</math>, we will take any prefix array <math>P(c,A)</math> and compute <math>P_j - P_i</math>. Notice that just as we can use any antiderivative <math>F</math> because the constant cancels out, we can use any prefix sum array because the initial value cancels out. (Note our use of the [[left half-open interval]].) |
| + | |||
| + | ''Proof'': <math>P_j = c + \sum_{k=0}^{j-1} A_k</math> and <math>P_i = c + \sum_{k=0}^{i-1} A_k</math>. Subtracting gives <math>P_j - P_i = \sum_{k=0}^{j-1} A_k - \sum_{k=0}^{i-1} A_k = \sum_{k=i}^{j-1} A_k</math> as desired. <math>_{\blacksquare}</math> | ||
| + | |||
| + | This is best illustrated ''via'' example. Let <math>A = [9,2,6,3,1,5,0,7]</math> as before. Take <math>P(0,A) = [0, 9, 11, 17, 20, 21, 26, 26, 33]</math>. Then, suppose we want <math>A_2 + A_3 + A_4 + A_5 = 6 + 3 + 1 + 5 = 15</math>. We can compute this by taking <math>P_6 - P_2 = 26 - 11 = 15</math>. This is because <math>P_6 - P_2 = (0 + A_0 + A_1 + A_2 + A_3 + A_4 + A_5) - (0 + A_0 + A_1) = A_2 + A_3 + A_4 + A_5</math>. | ||
===Example: Counting Subsequences (SPOJ)=== | ===Example: Counting Subsequences (SPOJ)=== | ||
| Line 20: | Line 63: | ||
We will consider the problem {{SPOJ|SUBSEQ|Counting Subsequences}} from IPSC 2006. Here we are given an array of integers <math>S</math> and asked to find the number of contiguous subsequences of the array that sum to 47. | We will consider the problem {{SPOJ|SUBSEQ|Counting Subsequences}} from IPSC 2006. Here we are given an array of integers <math>S</math> and asked to find the number of contiguous subsequences of the array that sum to 47. | ||
| − | To solve this, we will first transform array <math>S</math> into its prefix sum array <math>P</math>. Notice that the sum of each contiguous subsequence <math>S_i + S_{i+1} + S_{i+2} + ... + S_{j-1}</math> corresponds to the difference of two elements of <math>P</math>, that is, <math>P_j - P_i</math>. So what we want to find is the number of pairs <math>(i,j)</math> with <math>P_j - P_i = 47</math> and <math>i < j</math>. (Note that if <math>i > j</math>, we will instead get a subsequence with sum -47.) | + | To solve this, we will first transform array <math>S</math> into its prefix sum array <math>P(0,S)</math>. Notice that the sum of each contiguous subsequence <math>S_i + S_{i+1} + S_{i+2} + ... + S_{j-1}</math> corresponds to the difference of two elements of <math>P</math>, that is, <math>P_j - P_i</math>. So what we want to find is the number of pairs <math>(i,j)</math> with <math>P_j - P_i = 47</math> and <math>i < j</math>. (Note that if <math>i > j</math>, we will instead get a subsequence with sum -47.) |
However, this is quite easy to do. We sweep through <math>P</math> from left to right, keeping a [[map]] of all elements of <math>P</math> we've seen so far, along with their frequencies; and for each element <math>P_j</math> we count the number of times <math>P_j - 48</math> has appeared so far, by looking up that value in our map; this tells us how many contiguous subsequences ending at <math>S_{j-1}</math> have sum 47. And finally, adding the number of contiguous subsequences with sum 47 ending at each entry of <math>S</math> gives the total number of such subsequences in the array. Total time taken is <math>O(N)</math>, if we use a [[hash table]] implementation of the map. | However, this is quite easy to do. We sweep through <math>P</math> from left to right, keeping a [[map]] of all elements of <math>P</math> we've seen so far, along with their frequencies; and for each element <math>P_j</math> we count the number of times <math>P_j - 48</math> has appeared so far, by looking up that value in our map; this tells us how many contiguous subsequences ending at <math>S_{j-1}</math> have sum 47. And finally, adding the number of contiguous subsequences with sum 47 ending at each entry of <math>S</math> gives the total number of such subsequences in the array. Total time taken is <math>O(N)</math>, if we use a [[hash table]] implementation of the map. | ||
Revision as of 08:16, 19 December 2011
Given an array of numbers, we can construct a new array by replacing each element by the difference between itself and the previous element, except for the first element, which we simply ignore. This is called the difference array, because it contains the first differences of the original array. We will denote the difference array of array  by
by 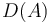 . For example, the difference array of
. For example, the difference array of ![A = [9, 2, 6, 3, 1, 5, 0, 7]](/wiki/images/math/7/f/9/7f9d88c652b184dc4db1a19714f6dd80.png) is
is ![D(A) = [2-9, 6-2, 3-6, 1-3, 5-1, 0-5, 7-0]](/wiki/images/math/e/3/5/e35ce6a5ac5351ad3daf63f72445d05b.png) , or
, or ![[-7, 4, -3, -2, 4, -5, 7]](/wiki/images/math/a/d/d/add580769fa99a870317b923383072b7.png) .
.
We see that the difference array can be computed in linear time from the original array, and is shorter than the original array by one element. Here are implementations in C and Haskell. (Note that the Haskell implementation actually takes a list, not an array, and will work fine for infinite lists.)
// D must have enough space for n-1 ints void difference_array(int* A, int n, int* D) { for (int i = 0; i < n-1; i++) D[i] = A[i+1] - A[i]; }
d :: [Int] -> [Int] -- NB: The general type signature should be (Num a) => [a] -> [a] d a = zipWith (-) (tail a) a
The prefix sum array is the opposite of the difference array. Given an array of numbers  and an arbitrary constant
and an arbitrary constant  , we first append
, we first append  onto the front of the array, and then replace each element with the sum of itself and all the elements preceding it. For example, if we start with
onto the front of the array, and then replace each element with the sum of itself and all the elements preceding it. For example, if we start with ![A = [9, 2, 6, 3, 1, 5, 0, 7]](/wiki/images/math/7/f/9/7f9d88c652b184dc4db1a19714f6dd80.png) , and choose to append the arbitrary value
, and choose to append the arbitrary value 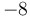 to the front, we obtain
to the front, we obtain ![P(-8, A) = [-8, -8+9, -8+9+2, -8+9+2+6, ..., -8+9+2+6+3+1+5+0+7]](/wiki/images/math/3/0/a/30a6494f688a01d72adad9f368016095.png) , or
, or ![[-8, 1, 3, 9, 12, 13, 18, 18, 25]](/wiki/images/math/5/c/c/5cc1dad3f6d3c0ccea7d7d3dd92c5bc8.png) . Computing the prefix sum array can be done in linear time as well, and the prefix sum array is longer than the original array by one element:
. Computing the prefix sum array can be done in linear time as well, and the prefix sum array is longer than the original array by one element:
// P must have enough space for n+1 ints void prefix_sum_array(int c, int* A, int n, int* P) { P[0] = c; for (int i = 0; i < n; i++) P[i+1] = P[i] + A[i]; }
p :: Int -> [Int] -> [Int] -- NB: The general type signature should be (Num a) => a -> [a] -> [a] p = scanl (+) -- NB: This is the same as p c a = scanl (+) c a
Note that every array has an infinite number of possible prefix sum arrays, since we can choose whatever value we want for  . For convenience, we usually choose
. For convenience, we usually choose 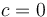 . However, changing the value of
. However, changing the value of  has only the effect of shifting all the elements of
has only the effect of shifting all the elements of 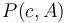 by a constant. For example,
by a constant. For example, ![P(15, A) = [15, 24, 26, 32, 35, 36, 41, 41, 48]](/wiki/images/math/2/f/5/2f55d6c3a47d61dae3b77320f34e8d9d.png) . However, each element of
. However, each element of 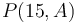 is exactly 23 more than the corresponding element from
is exactly 23 more than the corresponding element from 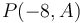 .
.
The functions 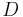 and
and  carry out reverse processes. Given an nonempty zero-indexed array
carry out reverse processes. Given an nonempty zero-indexed array  :
:
-
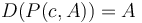 for any
for any  . For example, taking the difference array of
. For example, taking the difference array of ![P(-8, A) = [-8, 1, 3, 9, 12, 13, 18, 18, 25]](/wiki/images/math/0/2/b/02b6898dffbc07ad061a917cb0a015c4.png) gives
gives ![[9, 2, 6, 3, 1, 5, 0, 7]](/wiki/images/math/a/3/e/a3e4109270a19cac82c7e91bec7564e4.png) , that is, it restores the original array
, that is, it restores the original array  .
. -
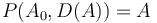 . Thus, taking
. Thus, taking ![D(A) = [-7, 4, -3, -2, 4, -5, 7]](/wiki/images/math/f/4/4/f4480db6ad3c47e96c7874fcfcea1336.png) and
and 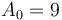 (initial element of
(initial element of  ), we have
), we have ![P(A_0, D(A)) = [9, 2, 6, 3, 1, 5, 0, 7]](/wiki/images/math/9/7/a/97a41ef3e4d9b2e3dde402ac06122ea8.png) , again restoring the original array
, again restoring the original array  .
.
Analogy with calculus
These two processes—computing the difference array, and computing a prefix sum array—are the discrete equivalents of differentiation and integration in calculus, which operate on continuous domains. An entry in an array is like the value of a function at a particular point.
- Reverse processes:
-
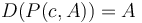 for any
for any  . Likewise
. Likewise 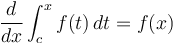 for any
for any  .
. -
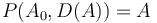 . Likewise
. Likewise 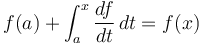 .
.
-
- Uniqueness:
- A differentiable function
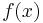 can only have one derivative,
can only have one derivative, 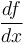 . An array
. An array  can only have one difference array,
can only have one difference array, 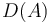 .
. - A continuous function
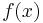 has an infinite number of antiderivatives,
has an infinite number of antiderivatives, 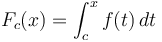 , where
, where  can be any number in its domain, but they differ only by a constant (their graphs are vertical translations of each other). An array
can be any number in its domain, but they differ only by a constant (their graphs are vertical translations of each other). An array  has an infinite number of prefix arrays
has an infinite number of prefix arrays 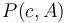 , but they differ only by a constant (at each entry).
, but they differ only by a constant (at each entry).
- A differentiable function
- Given some function
![f:[a,b]\to\mathbb{R}](/wiki/images/math/3/3/2/332d0f0f6103ad3c4ec22d3af5b36e7c.png) , and the fact that
, and the fact that 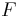 , an antiderivative of
, an antiderivative of  , satisfies
, satisfies 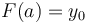 , we can uniquely reconstruct
, we can uniquely reconstruct 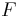 . That is, even though
. That is, even though  has an infinite number of antiderivatives, we can pin it down to one once we are given the value the antiderivative is supposed to attain on the left edge of
has an infinite number of antiderivatives, we can pin it down to one once we are given the value the antiderivative is supposed to attain on the left edge of  's domain. Likewise, given some array
's domain. Likewise, given some array  and the fact that
and the fact that  , a prefix sum array of
, a prefix sum array of  , satisfies
, satisfies 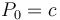 , we can uniquely reconstruct
, we can uniquely reconstruct  .
. - Effect on length:
-
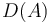 is shorter than
is shorter than  by one element. Differentiating
by one element. Differentiating ![f:[a,b] \to \mathbb{R}](/wiki/images/math/3/3/2/332d0f0f6103ad3c4ec22d3af5b36e7c.png) gives a function
gives a function 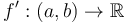 (shortens the closed interval to an open interval).
(shortens the closed interval to an open interval). -
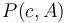 is longer than
is longer than  by one element. Integrating
by one element. Integrating 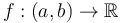 gives a function
gives a function ![F:[a,b] \to \mathbb{R}](/wiki/images/math/1/9/b/19b17cac5b2437be7e4aa88212b6ddc4.png) (lengthens the open interval to a closed interval).
(lengthens the open interval to a closed interval).
-
Because of these similarities, we will speak simply of differentiating and integrating arrays. An array can be differentiated multiple times, but eventually it will shrink to length 0. An array can be integrated any number of times.
Use of prefix sum array
The Fundamental Theorem of Calculus also has an analogue, which is why the prefix sum array is so useful. To compute an integral 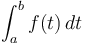 , which is like a continuous kind of sum of an infinite number of function values
, which is like a continuous kind of sum of an infinite number of function values 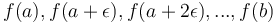 , we take any antiderivative
, we take any antiderivative 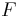 , and compute
, and compute  . Likewise, to compute the sum of values
. Likewise, to compute the sum of values 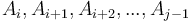 , we will take any prefix array
, we will take any prefix array 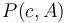 and compute
and compute  . Notice that just as we can use any antiderivative
. Notice that just as we can use any antiderivative 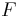 because the constant cancels out, we can use any prefix sum array because the initial value cancels out. (Note our use of the left half-open interval.)
because the constant cancels out, we can use any prefix sum array because the initial value cancels out. (Note our use of the left half-open interval.)
Proof: 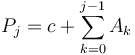 and
and 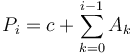 . Subtracting gives
. Subtracting gives 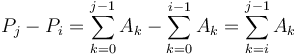 as desired.
as desired. 
This is best illustrated via example. Let ![A = [9,2,6,3,1,5,0,7]](/wiki/images/math/7/f/9/7f9d88c652b184dc4db1a19714f6dd80.png) as before. Take
as before. Take ![P(0,A) = [0, 9, 11, 17, 20, 21, 26, 26, 33]](/wiki/images/math/c/4/7/c473217b3594e5fed86c3fbef7cc3894.png) . Then, suppose we want
. Then, suppose we want 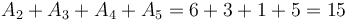 . We can compute this by taking
. We can compute this by taking 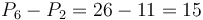 . This is because
. This is because 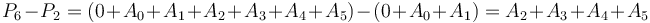 .
.
Example: Counting Subsequences (SPOJ)
Computing the prefix sum array is rarely the most difficult part of a problem. Instead, the prefix sum array is kept on hand because the algorithm to solve the problem makes frequent reference to range sums.
We will consider the problem Counting Subsequences from IPSC 2006. Here we are given an array of integers  and asked to find the number of contiguous subsequences of the array that sum to 47.
and asked to find the number of contiguous subsequences of the array that sum to 47.
To solve this, we will first transform array  into its prefix sum array
into its prefix sum array 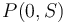 . Notice that the sum of each contiguous subsequence
. Notice that the sum of each contiguous subsequence 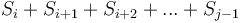 corresponds to the difference of two elements of
corresponds to the difference of two elements of  , that is,
, that is,  . So what we want to find is the number of pairs
. So what we want to find is the number of pairs 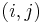 with
with 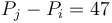 and
and 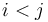 . (Note that if
. (Note that if 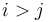 , we will instead get a subsequence with sum -47.)
, we will instead get a subsequence with sum -47.)
However, this is quite easy to do. We sweep through  from left to right, keeping a map of all elements of
from left to right, keeping a map of all elements of  we've seen so far, along with their frequencies; and for each element
we've seen so far, along with their frequencies; and for each element 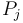 we count the number of times
we count the number of times  has appeared so far, by looking up that value in our map; this tells us how many contiguous subsequences ending at
has appeared so far, by looking up that value in our map; this tells us how many contiguous subsequences ending at 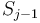 have sum 47. And finally, adding the number of contiguous subsequences with sum 47 ending at each entry of
have sum 47. And finally, adding the number of contiguous subsequences with sum 47 ending at each entry of  gives the total number of such subsequences in the array. Total time taken is
gives the total number of such subsequences in the array. Total time taken is  , if we use a hash table implementation of the map.
, if we use a hash table implementation of the map.