Lowest common ancestor
The lowest common ancestor or least common ancestor (LCA) of a nonempty set of nodes in a rooted tree is the unique node of greatest depth that is an ancestor of every node in the set. (In biology, this corresponds to the most recent common ancestor of a set of organisms.) We will denote the LCA of a set of nodes 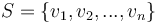 by
by 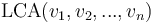 or by
or by 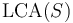 .
.
Contents
Properties
The proofs of these properties are left as an exercise to the reader.
-
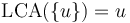 .
. -
 is an ancestor of
is an ancestor of  if and only if
if and only if 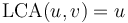 .
. - If neither
 nor
nor  is an ancestor of the other, than
is an ancestor of the other, than  and
and  lie in different immediate subtrees of
lie in different immediate subtrees of 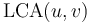 . (That is, the child of the
. (That is, the child of the 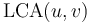 of which
of which  is a descendant is not the same as the child of the
is a descendant is not the same as the child of the 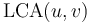 of which
of which  is a descendant.) Furthermore, the
is a descendant.) Furthermore, the 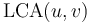 is the only node in the tree for which this is true.
is the only node in the tree for which this is true. - The entire set of common ancestors of
 is given by
is given by 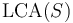 and all of its ancestors (all the way up to the root of the tree). In particular, every common ancestor of
and all of its ancestors (all the way up to the root of the tree). In particular, every common ancestor of  is an ancestor of
is an ancestor of 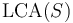 .
. -
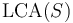 precedes all nodes in
precedes all nodes in  in the tree's preordering, and follows all nodes in
in the tree's preordering, and follows all nodes in  in the tree's postordering.
in the tree's postordering. - If
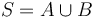 with
with  and
and  both nonempty, then
both nonempty, then 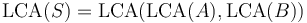 . For example,
. For example, 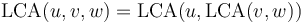 . (The LCA shares this property with the similar-sounding lowest common multiple and greatest common divisor; and this property can be used to compute the LCA of arbitrarily large sets using only binary LCA computations.)
. (The LCA shares this property with the similar-sounding lowest common multiple and greatest common divisor; and this property can be used to compute the LCA of arbitrarily large sets using only binary LCA computations.) -
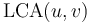 is the unique highest (least deep) node on the unique simple path from
is the unique highest (least deep) node on the unique simple path from  to
to  .
. -
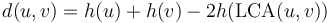 , where
, where 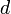 represents the distance between two nodes and
represents the distance between two nodes and 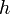 represents the height of a node.
represents the height of a node.
Algorithms and variations
Finding the lowest common ancestor of a given pair of nodes in a given tree is an extensively studied problem.
Naive
The naive algorithm runs in 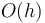 time, where
time, where 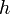 is the height of the tree. It works by computing the sequences
is the height of the tree. It works by computing the sequences 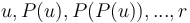 (where
(where  represents the parent of a node and
represents the parent of a node and  the root of the tree) and
the root of the tree) and 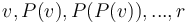 for the two given nodes
for the two given nodes  and
and  . The first element of the longest common suffix of these two sequences is then trivially the LCA. Note that if the tree is well-balanced, then this approach will actually perform quite well (around
. The first element of the longest common suffix of these two sequences is then trivially the LCA. Note that if the tree is well-balanced, then this approach will actually perform quite well (around 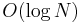 time per query, where
time per query, where  is the size of the tree).
is the size of the tree).
Offline
If we want to find the LCAs of multiple pairs of nodes in the same tree, and we know all the pairs of nodes in advance, then we can use Tarjan's offline LCA algorithm. It is not easy to picture how this algorithm works, but it is quite easy to implement it. It uses  disjoint set operations, so can easily be made to run in
disjoint set operations, so can easily be made to run in 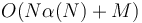 time (where
time (where 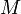 is the size of the input), barely slower than linear. It is also possible to implement it so that it runs in
is the size of the input), barely slower than linear. It is also possible to implement it so that it runs in 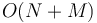 time (that is, linear)[1], but this is unlikely to give faster code in practice.
time (that is, linear)[1], but this is unlikely to give faster code in practice.
Reduction to RMQ
It is possible to solve any instance of the LCA problem by reducing it to an instance of the range minimum query (RMQ) problem. In particular, given a rooted tree, we can construct an array with the property that the LCA of any pair of nodes in the tree can be determined by finding the RMQ of some segment of that array.
The correct way to construct this array may be described intuitively as "walking" around the tree. The following pseudocode expresses exactly how this "walk" is constructed, using a depth-first search:
walk(node u)
print u
for v ∈ u's children
walk(v)
print u
In other words, a node with  children is visited
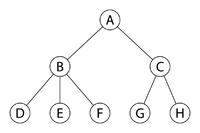
children is visited 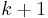 times; once when we first encounter it by recursing down from its parent, and once again after each of its child subtrees has been fully explored. In the example tree shown to the right, if we assume that we visit children in left-to-right order as shown on the diagram, we obtain the ordering ABDBEBFBACGCHCA. Observe that this is the same order that we would obtain if, on the diagram, we started out on the left side of the circle containing the letter "A", and started walking down along the edge between A and B, and walked "all the way around" the tree, writing down the label of each node we touched along the way. This traversal also corresponds to an Eulerian circuit of the tree, assuming that we replace each undirected edge with a pair of directed edges. Since a tree with
times; once when we first encounter it by recursing down from its parent, and once again after each of its child subtrees has been fully explored. In the example tree shown to the right, if we assume that we visit children in left-to-right order as shown on the diagram, we obtain the ordering ABDBEBFBACGCHCA. Observe that this is the same order that we would obtain if, on the diagram, we started out on the left side of the circle containing the letter "A", and started walking down along the edge between A and B, and walked "all the way around" the tree, writing down the label of each node we touched along the way. This traversal also corresponds to an Eulerian circuit of the tree, assuming that we replace each undirected edge with a pair of directed edges. Since a tree with  nodes has
nodes has 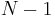 edges, and each edge is traversed once in each direction, this Eulerian circuit has length
edges, and each edge is traversed once in each direction, this Eulerian circuit has length 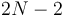 ; and hence it contains
; and hence it contains 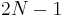 vertices.
vertices.
This traversal has the very useful property that between (inclusive) any occurrence of node  in it and any occurrence of node
in it and any occurrence of node  in it,
in it, 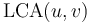 is guaranteed to appear at least once, and no other node with depth less than or equal to that of
is guaranteed to appear at least once, and no other node with depth less than or equal to that of 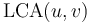 will appear at all. For example, consider the positions of D and F in the traversal ABDBEBFBACGCHCA; we see that their LCA, that is, B, occurs between them, and that the nodes C and A do not occur at all.
will appear at all. For example, consider the positions of D and F in the traversal ABDBEBFBACGCHCA; we see that their LCA, that is, B, occurs between them, and that the nodes C and A do not occur at all.
- Proof: First, we show that the LCA occurs, in two cases:
- If the LCA is
 or
or  itself, then without loss of generality assume it is
itself, then without loss of generality assume it is  . Then, clearly, between any occurrence of
. Then, clearly, between any occurrence of  and any occurrence of
and any occurrence of  (inclusive) we find an occurrence of the LCA, since the LCA is
(inclusive) we find an occurrence of the LCA, since the LCA is  itself.
itself. - Otherwise,
 and
and  are in different subtrees of their LCA
are in different subtrees of their LCA 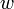 . Let
. Let 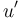 and
and 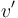 be the roots of these respective subtrees, and children of
be the roots of these respective subtrees, and children of 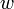 . From the
. From the walkfunction above, it is clear that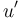 is first visited before any of its proper descendants (including
is first visited before any of its proper descendants (including  ), and after it is last visited, none of its proper descendants will ever be visited again; the same is true of
), and after it is last visited, none of its proper descendants will ever be visited again; the same is true of 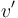 and its children, including
and its children, including  . Since neither
. Since neither  nor
nor  is a descendant of the other, it is clear that, without loss of generality, all the descendants in
is a descendant of the other, it is clear that, without loss of generality, all the descendants in 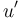 are visited before descendants of
are visited before descendants of 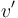 . But
. But 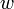 is visited immediately after the last occurrence of
is visited immediately after the last occurrence of 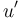 , so it will occur between any descendant of
, so it will occur between any descendant of 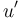 and any descendant of
and any descendant of 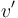 . Therefore, it will occur between any occurrence of
. Therefore, it will occur between any occurrence of  and any occurrence of
and any occurrence of  .
.
- If the LCA is
- Now, consider nodes other than the LCA that have depth less than or equal to that of the LCA. Call such a node
 .
.  is obviously not a descendant of the LCA. Notice that
is obviously not a descendant of the LCA. Notice that  can only be visited between the entry and exit of the instance of
can only be visited between the entry and exit of the instance of walkwith the LCA as argument, and that too can only be visited during that time. However, only descendants of the LCA can be visited during this time, so
too can only be visited during that time. However, only descendants of the LCA can be visited during this time, so  cannot possibly be visited.
cannot possibly be visited. 
Now construct the array  by replacing each node in the traversal described above by its depth. The example tree gives
by replacing each node in the traversal described above by its depth. The example tree gives ![A = [0, 1, 2, 1, 2, 1, 2, 1, 0, 1, 2, 1, 2, 1, 0]](/wiki/images/math/0/f/c/0fccce335b76becc0459bd76a0a57568.png) . This array has size
. This array has size 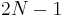 . Given
. Given  and
and  , locate two elements in
, locate two elements in  , one that corresponds to
, one that corresponds to  , and one that corresponds to
, and one that corresponds to  . (This can be done in constant time using a lookup table that we compute while we are doing the traversal). We know from the preceding property that the LCA is the unique shallowest node corresponding to any element located between these two elements. Therefore, by finding the position of some minimum element in this range, we will locate the LCA. So if we can answer range minimum queries in
. (This can be done in constant time using a lookup table that we compute while we are doing the traversal). We know from the preceding property that the LCA is the unique shallowest node corresponding to any element located between these two elements. Therefore, by finding the position of some minimum element in this range, we will locate the LCA. So if we can answer range minimum queries in 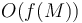 time (where
time (where 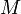 is the size of the array) after
is the size of the array) after 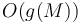 preprocessing time, then we can use this technique to answer LCA queries in
preprocessing time, then we can use this technique to answer LCA queries in 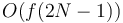 time and
time and 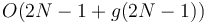 preprocessing time. We do so by constructing the array
preprocessing time. We do so by constructing the array  using
using 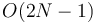 time and space, carrying out whatever preprocessing on
time and space, carrying out whatever preprocessing on  our RMQ algorithm requires, and then converting each LCA query into an RMQ.
our RMQ algorithm requires, and then converting each LCA query into an RMQ.
Since there is an algorithm that solves RMQ with linear preprocessing time and constant query time, the LCA problem can also be solved in linear preprocessing time and constant query time.
With heavy-light decomposition
The heavy-light decomposition provides an easy way to ascend a tree quickly, which allows an adaptation of the naive algorithm to run in 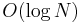 time after linear preprocessing time. This is not asymptotically optimal, as the LCA-to-RMQ reduction discussed in the previous section allows queries to be performed in constant time. However, if the decomposition is being used for other purposes than simply answering LCA queries, then the LCA query time might not dominate the overall runtime, anyway.
time after linear preprocessing time. This is not asymptotically optimal, as the LCA-to-RMQ reduction discussed in the previous section allows queries to be performed in constant time. However, if the decomposition is being used for other purposes than simply answering LCA queries, then the LCA query time might not dominate the overall runtime, anyway.
Dynamic
In the fully dynamic variant of the LCA problem, we must be prepared to handle LCA queries intermixed with operations that change the tree (that is, rearrange the tree by adding and removing edges). In general, we suppose that we have a forest of  nodes in which we can arbitrarily link together two nodes from different trees, cut an edge (thus dividing a tree into two trees), or change the root of a tree on a whim, and the answer to an LCA query is either a node or the finding that the two nodes given are in different trees.
nodes in which we can arbitrarily link together two nodes from different trees, cut an edge (thus dividing a tree into two trees), or change the root of a tree on a whim, and the answer to an LCA query is either a node or the finding that the two nodes given are in different trees.
This variant can be solved using 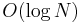 time for all modifications and queries. This is done by maintaining the forest using the dynamic trees data structure with partitioning by size; this then maintains a heavy-;light decomposition of each tree, and allows LCA queries to be carried out in logarithmic time as discussed in the previous section.
time for all modifications and queries. This is done by maintaining the forest using the dynamic trees data structure with partitioning by size; this then maintains a heavy-;light decomposition of each tree, and allows LCA queries to be carried out in logarithmic time as discussed in the previous section.
References
- ↑ Gabow, H. N.; Tarjan, R. E. (1983), "A linear-time algorithm for a special case of disjoint set union", Proceedings of the 15th ACM Symposium on Theory of Computing (STOC), pp. 246–251, doi:10.1145/800061.808753.