IEEE 754
IEEE (Institute of Electrical and Electronics Engineers) 754 is a floating-point computation standard. It is universal among personal computers, and also commonplace among other devices.
Contents
Binary32 and binary64 data types[edit]
IEEE 754 defines, among other things, two formats for the binary encoding of floating-point numbers. Binary32, also known as single precision:[1]
- is 32 bits wide;
- has a precision of up to 24 bits (about 7 digits);
- can store positive and negative numbers of absolute value as small as about 10-45 and as large as about 1038, as well as zero;
- supports the representation of positive infinity, negative infinity, and "not a number" (NaN) values.
Binary64, also known as double precision, is wider, but otherwise similar, with a total size of 64 bits (up to 53 bits precision, or about 16 digits), and support for absolute values as small as 10-323 and as large as about 10308.
Basic anatomy[edit]
Any nonzero real number can be expressed in scientific notation as 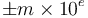 , where
, where  is an integer and
is an integer and 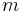 , the mantissa, satisfies
, the mantissa, satisfies 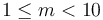 . In analogy, the binary32 and binary64 types represent nonzero real numbers as
. In analogy, the binary32 and binary64 types represent nonzero real numbers as 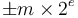 , where
, where  is an integer and
is an integer and 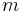 , the significand, satisfies
, the significand, satisfies 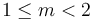 .
.
To represent the sign, a sign bit is used; this is the leading bit in a binary32 or binary64 word and is 0 if the real number is positive or 1 if it is negative. In a binary32, the next 8 bits are used to store the exponent, whereas in a binary64, it is the next 11 bits that are used for this purpose. Since it is desirable to be able to represent both numbers that are much larger than 1 and numbers that are much smaller than 1 (in absolute value), both positive and negative exponents must be supported. However, negative exponents are not stored according to the two's complement convention that is almost always used for integer data types. Instead, 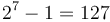 is added to the binary32 exponent and
is added to the binary32 exponent and 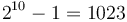 is added to the binary64 exponent, which is then stored as a positive number. For example, the bit sequence
is added to the binary64 exponent, which is then stored as a positive number. For example, the bit sequence 01101011, when used as the exponent in a binary32 number, does not represent the exponent 011010112 (that is, 107). Instead it represents the exponent 107 - 127 = -20. (The value 107 is known as the biased exponent.) The significand is stored in the last 23 bits (in a binary32) or the last 52 bits (in a binary64). Since the leading bit will always be 1 (as the significand is greater than or equal to 1, but less than 2), it is not stored at all, but rather implied. Thus, for example, the bit string 10000000000000000000000, if found in the significand part of a binary32, actually represents 1.100000000000000000000002, that is, the number 1.5.
Imprecision and limits[edit]
It is clear that the binary32 and binary64 types cannot represent all possible real numbers, as there are uncountably many of these. Indeed, they cannot even represent all possible real numbers within any given interval, because there are still uncountably many (whereas it is perfectly possible to define integer data types that can represent all integers in a given interval, as there are only finitely many of those). This fact is also evident from the foregoing discussion. The binary32 and binary64 (and all other floating-point types) are limited in both range and precision.
They are limited in range because only a finite number of different possible exponents are stored. For example, the exponent 300 is too large to be stored in the 8 bits of a binary32, though it will fit in a binary64; the exponent 3000 is too large for either type. Since there is a limit on how large an exponent we can store, and how small an exponent we can store, it follows that there are some real numbers that are simply too large to represent with binary32 or binary64, and others that are too small (in absolute value).
Of course, perhaps one should expect a limitation in range, because that is exactly what one finds with the signed and unsigned integer types in programming languages. On the other hand, programmers sometimes forget that precision is also limited. That is, when representing a real number as a binary32 or a binary64, any bits of the significand beyond those that will fit into the data type simply have to be truncated or rounded off. It follows, for example, that a number with a non-terminating binary expansion, such as 1/3, cannot be stored exactly; this number has binary expansion 0.010101...2 but when we store it in a binary32 or binary64 we have to discard all the bits that can't fit into the significand. Note that some numbers, such as 1/5, have terminating decimal expansions, but not terminating binary expansions. The 23 bits allocated to the significand in the binary32 type, plus the implied leading one, add up to 24 bits of precision, or about 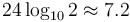 digits. The 52+1 bits in the binary64 type correspond to about
digits. The 52+1 bits in the binary64 type correspond to about 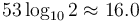 digits. For even greater precision, one must usually use arbitrary-precision arithmetic.
digits. For even greater precision, one must usually use arbitrary-precision arithmetic.
Nonreal values[edit]
Not only do the binary32 and binary64 types fail to represent all possible real numbers, but they also represent some values that are not real numbers at all. These are positive infinity, negative infinity, and NaN (not a number). The sign bit is zero for positive infinity and one for negative infinity; it is irrelevant for a NaN. For both infinities as well as NaNs, the exponent is set to all ones (corresponding to the value 255 for a binary32 or 2047 for a binary64). If the significand consists entirely of zeroes, the binary32 or binary64 represents a positive or negative infinity (depending on the sign bit). If it is nonzero but its leading bit is a zero, then it represents an sNaN (signalling NaN), which ordinarily means that any attempt to involve it in a calculation will trigger an exception. If the leading bit is one, on the other hand, the value stored is a qNaN (quiet NaN). These do not trigger exceptions, but they "taint" all calculations that involve them (for example, 1 + qNaN = qNaN).
The following produce infinities, or sometimes raise floating-point exceptions which may crash the program, depending on the circumstances under which they arise:
- Any operation that produces a result too large to fit in the largest (or largest negative) representable real. Adding or multiplying two extremely large numbers. Dividing a very large number by a very small number. Taking the exponential of a very large number. Computing the tangent of an angle very close to an odd multiple of
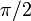 .
. - Dividing a positive number by zero, giving positive infinity.
- Dividing a negative number by zero, giving negative infinity.
- Taking the logarithm of zero (negative infinity).
The following produce NaNs:
- Any operation that involves a NaN as an operand.
- Any operation whose result is indeterminate. Dividing zero by zero. Multiplying zero by infinity. Dividing infinity by infinity. Subtracting infinity from infinity.
- Any operation whose result is a nonreal complex number. Taking the logarithm of a negative number. Taking the square root of a negative number. Taking the inverse sine or inverse cosine of a number whose absolute value exceeds one.
Positive infinity is considered to be greater than any finite value, and all finite values are considered to be greater than negative infinity. Any comparison involving a NaN, on the other hand, evaluates to false. In fact, if  is a NaN, even
is a NaN, even  is false.
is false.
Zero and subnormal values[edit]
We have not yet discussed the representation of zero. Zero cannot be expressed as 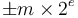 for any
for any 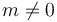 , and we also have no way to denote a zero significand. This problem is solved by specifying that whenever a binary32 or binary64's exponent field is actually zero (that is, a bit string of 8 or 11 zeroes, respectively), we stop assuming that the significand carries a leading implied 1. Thus, when the exponent field is zero in a binary32, for example, a significand of
, and we also have no way to denote a zero significand. This problem is solved by specifying that whenever a binary32 or binary64's exponent field is actually zero (that is, a bit string of 8 or 11 zeroes, respectively), we stop assuming that the significand carries a leading implied 1. Thus, when the exponent field is zero in a binary32, for example, a significand of 10000000000000000000000 actually represents 1.00000000000000000000002, and the number represented is 2-127.
Under this representation, setting both the exponent and the significand to all zeroes gives the value zero. If the exponent is zero, but the significand is nonzero, then we have a nonzero number that has less than the usual amount of precision; a binary32 number of this kind can only have up to 23 bits of precision rather than the usual 24 (and, the smaller it is, the less precise), and a binary64 can only have up to 52 bits of precision rather than the usual 53. These less-precise-than-usual numbers are called subnormal (or denormal). Zero is not considered subnormal.
Signed zero[edit]
Note that there are two possible representations for zero. The one in which the sign bit is 0 is called positive zero, and the one in which the sign bit is 1 is called negative zero. The following rules apply:
- Positive zero and negative zero compare equal. Specifically, positive zero is not considered to be greater than negative zero.
- When multiplying two numbers, at least one of which is zero, the signs are also multiplied; for example, multiplying positive zero by any negative value (except negative infinity) gives negative zero.
- Likewise, when dividing zero by a nonzero number, the signs are also divided. This is true even when the divisor is infinite.
- When dividing a nonzero number by zero, the signs are also divided (and the result will be either positive infinity or negative infinity, accordingly).
- (+0) + (+0) = (+0) - (-0) = +0
- (-0) + (-0) = (-0) - (+0) = -0
- (+0) + (-0) = (-0) + (+0) = (+0) - (+0) = (-0) - (-0). They are all equal to +0, except in round toward negative infinity mode, in which case they all equal -0. In fact, the same is true of
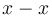 or
or 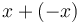 , for any real
, for any real  .
. - The square root of +0 is +0 and the square root of -0 is -0.
Summary[edit]
For a binary32 (binary64) value:
- The first bit is a sign bit, the next 8 (11) bits are the biased exponent, and the last 23 (52) bits are the significand;
- A biased exponent of zero represents either zero or a subnormal number. A biased exponent of 255 (2047), that is, all ones, represents either an infinite value or a NaN. Any biased exponent between 1 and 254 (2046) represents an actual exponent 127 (1023) less than itself. It follows that the smallest representable normal (not subnormal) number is 2-126 (2-1022), and the largest representable exponent is 127 (1023), so that if we fill the significand with all ones, we get a value that is almost 2128 (21024) as the largest representable real number.
- Note that when the leading bit of the biased exponent is a 0 (that is, the biased exponent is 127 (1023) or less), the actual exponent is negative, whereas if it is a 1, then the actual exponent is positive.
- When the biased exponent is zero, the a significand consisting entirely of zeroes represents zero, whereas a nonzero significand represents a subnormal number. There exist positive zero and negative zero.
- When the biased exponent is 255 (2047):
- ... and the significand is all zeroes, the value is either positive or negative infinity, depending on sign;
- ... and the significand's leading bit is zero, but some other bit is nonzero, the value is an sNaN;
- ... and the significand's leading bit is one, the value is a qNaN.
Programming language support[edit]
Expansion of this section would be welcome.
The binary32 and binary64 types are ubiquitous among microprocessors. Naturally, they also enjoy extensive programming language support:
- C and C++: In nearly all implementations, the data type
floatis a binary32 value, and the data typedoubleis a binary64 value. Although this is not required by the standard, most programmers are unlikely to ever come across a machine that deviates from this, simply by virtue of C tending to be "close to the machine" and the fact that virtually all machines natively support IEEE 754. - Java:
floatanddoublebehave exactly like binary32 and binary64, but the standard does not require that their internal representations match those of binary32 and binary64.[2] - JavaScript: ECMA 262 prescribes that a JavaScript number behaves as a binary64.[3]
- .NET: The Common Type System provides the
System.SingleandSystem.Doubletypes, that correspond to binary32 and binary64, respectively.[4] - O'Caml: Uses binary64[5]
- Pascal: The ANSI/ISO Pascal standard provides only for a
realtype. However, for much of history, the only important Pascal implementation was Borland's Turbo Pascal; it had asingletype, a binary32; and adoubletype, a binary64. (Even on older IA-32 processors lacking numeric coprocessors, software emulation was provided to ensure that these data types behaved according to IEEE 754.) The newer Free Pascal compiler guarantees thatsingleanddoublemap to binary32 and binary64, respectively.[6] - Ruby: uses the underlying architecture's native double-precision floating point type.[7] Note that Ruby (unlike C) has probably never been ported to an architecture on which this is not a binary64.
The R5RS standard for the Scheme programming language recommends the use of IEEE 754, but does not require it. The Haskell98 report recommends, but does not require, that Haskell's built-in Float type be able to represent at least the range of values of a binary32, and likewise with Double and binary64.
In other programming languages, there is often no guarantee of finding types corresponding to binary32 or binary64, but it is still overwhelmingly more likely than not that the floating-point types on any given implementation of any given programming language correspond to binary32 or binary64. (Some programming languages, however, also provide arbitrary-precision or fixed-point real types; these are not covered by IEEE 754.)
References[edit]
- ↑ Intel Corporation. Intel® 64 and IA-32 Architectures Developer's Manual: Combined Volumes. Section 4.2.2 Floating-Point Data Types. Retrieved from http://www.intel.com/content/dam/www/public/us/en/documents/manuals/64-ia-32-architectures-software-developer-manual-325462.pdf
- ↑ Sun Microsystems, Inc. (2000). Java Language Specification, Second Edition. Section 4.2.3 Floating-Point Types, Formats, and Values
- ↑ ECMAScript Language Specification, Edition 5.1. (2011). Section 8.5 The Number Type. Retrieved from http://www.ecma-international.org/publications/files/ECMA-ST/Ecma-262.pdf
- ↑ Common Language Infrastructure (CLI), Partitions I to V, Second Edition. (2002). Section 8.2.2 Built-in Types. Retrieved from http://www.ecma-international.org/publications/files/ECMA-ST-WITHDRAWN/ECMA-335,%202nd%20edition,%20December%202002.pdf
- ↑ http://caml.inria.fr/pub/docs/manual-ocaml/libref/Pervasives.html
- ↑ Michaël Van Canneyt. (2011). Free Pascal Programmer's Guide. Retrieved from http://www.freepascal.org/docs-html/prog/progsu144.html
- ↑ http://www.ruby-doc.org/core-1.9.3/Float.html