Heavy-light decomposition
The heavy-light (H-L) decomposition of a rooted tree is a method of partitioning of the vertices of the tree into disjoint paths (all vertices have degree two, except the endpoints of a path, with degree one) that gives important asymptotic time bounds for certain problems involving trees. It appears to have been introduced in passing in Sleator and Tarjan's analysis of the performance of the link-cut tree data structure.
Contents
Definition
The heavy-light decomposition of a tree 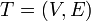 is a coloring of the tree's edges. Each edge is either heavy or light. To determine which, consider the edge's two endpoints: one is closer to the root, and one is further away. If the size of the subtree rooted at the latter is more than half that of the subtree rooted at the former, the edge is heavy. Otherwise, it is light.
is a coloring of the tree's edges. Each edge is either heavy or light. To determine which, consider the edge's two endpoints: one is closer to the root, and one is further away. If the size of the subtree rooted at the latter is more than half that of the subtree rooted at the former, the edge is heavy. Otherwise, it is light.
Properties
Denote the size of a subtree rooted at vertex  as
as 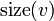 .
.
Suppose that a vertex  has two children
has two children  and
and  and the edges
and the edges  -
- and
and  -
- are both heavy. Then,
are both heavy. Then, 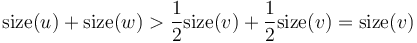 . This is a contradiction, since we know that
. This is a contradiction, since we know that 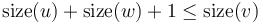 . (
. ( , of course, may have more than two children.) We conclude that there may be at most one heavy edge of all the edges joining any given vertex to its children.
, of course, may have more than two children.) We conclude that there may be at most one heavy edge of all the edges joining any given vertex to its children.
At most two edges incident upon a given vertex may then be heavy: the one joining it to its parent, and at most one joining it to a child. Consider the subgraph of the tree in which all light edges are removed. Then, all resulting connected components are paths (although some contain only one vertex and no edges at all) and two neighboring vertices' heights differ by one. We conclude that the heavy edges, along with the vertices upon which they are incident, partition the tree into disjoint paths, each of which is part of some path from the root to a leaf.
Suppose a tree contains  vertices. If we follow a light edge from the root, the subtree rooted at the resulting vertex has size at most
vertices. If we follow a light edge from the root, the subtree rooted at the resulting vertex has size at most 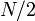 ; if we repeat this, we reach a vertex with subtree size at most
; if we repeat this, we reach a vertex with subtree size at most 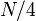 , and so on. It follows that the number of light edges on any path from root to leaf is at most
, and so on. It follows that the number of light edges on any path from root to leaf is at most 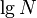 .
.
Applications
The utility of the H-L decomposition lies in that problems involving paths between nodes can often be solved more efficiently by "skipping over" heavy paths rather than considering each edge in the path individually. This is because long paths in trees that are very poorly balanced tend to consist mostly of heavy edges.
To "skip" from any node in the tree to the root:
while current_node ≠ root
if color(current_node,parent(current_node)) = light
current_node = parent(current_node)
else
current_node = skip(current_node)
In the above, color(u,v) represents the color (heavy or light) of the edge from u to v, parent(v) represents the parent of a node v, and skip(v) represents the parent of the highest (i.e., least deep) node that is located on the same heavy path as node v. (It is so named because it allows us to "skip" through heavy paths.) In order for the latter to be implemented efficiently, every node whose parent link is heavy must be augmented with a pointer to the result of the skip function, but that is trivial to achieve.
What is the running time of this fragment of code? There are most a logarithmic number of light edges on the path, each of which takes constant time to traverse. There are also at most a logarithmic number of heavy subpaths, since between each pair of adjacent heavy paths lies a light path. We spend at most a constant amount of time on each of these, so overall this "skipping" operation runs in logarithmic time.
This might not seem like much, but let's see how it can be used to solve a simple problem.
Lowest common ancestor
The H-L decomposition gives an efficient solution to the lowest common ancestor (LCA) problem. Consider first a naive solution:
function LCA(u,v)
while depth(u) < depth(v) and u ≠ v
v = parent(v)
while depth(u) > depth(v) and u ≠ v
u = parent(u)
while u ≠ v
u = parent(u)
v = parent(v)
return u
(In this code, u and v are the nodes whose LCA is desired.)
This solution can take time proportional to the height of the tree, which can be up to linear. However, we can use the "skip" operation of the H-L decomposition to do much better:
function LCA_improved(u,v)
let last = root
while u ≠ v
if depth(u) > depth(v)
swap(u,v)
if color(v,parent(v)) = light
last = root
v = parent(v)
else
last = v
v = skip(v)
if last = root
return u
else
return last
Here's how this code works: in each iteration of the while loop, the deeper of the two nodes is advanced up the tree (that is, if its parent link is light, it becomes its parent, otherwise it "skips", as previously described). Note that if the two nodes are equally deep, one of them still gets advanced; this is intentional and it does not matter which one is advanced. When the two nodes become equal, we are done.
Or are we? Suppose that the highest edges on the paths from each node to the LCA are light. Then, it is clear that the while loop ends with both nodes now pointing to the LCA, after having advanced through the respective light edges. If, however, one is heavy, there is a possibility that we "overshoot"; that is, that we end up at a node higher in the tree than the actual LCA. If this occurs, then the last advancement before its occurrence is from the actual LCA to the ending node (convince yourself of this by drawing a diagram if necessary), so that all we have to do is "remember" the last node visited in this case. That is what the last variable holds. (If both final links to the LCA are light, it is set to the root of the tree, which is otherwise impossible, to indicate this.) Notice that we do not have to consider the case in which both final links to the LCA are heavy, since this is impossible; two child links from a node cannot both be heavy, so these two heavy links would have to be the same link, making the child of that link a lower common ancestor (a contradiction).
Dynamic distance query
Now consider the following problem: A weighted, rooted tree is given followed by a large number of queries and modifications interspersed with each other. A query asks for the distance between a given pair of nodes and a modification changes the weight of a specified edge to a new (specified) value. How can the queries and modifications be performed efficiently?
First of all, we notice that the distance between nodes  and
and  is given by
is given by 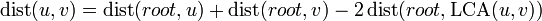 . We already know how to efficiently solve lowest common ancestor queries, so if we can efficiently solve queries of a node's distance from the root, a solution to this problem follows trivially.
. We already know how to efficiently solve lowest common ancestor queries, so if we can efficiently solve queries of a node's distance from the root, a solution to this problem follows trivially.
To solve this simpler problem of querying the distance from the root to a given node, we augment our walk procedure as follows: when following a light edge, simply add its distance to a running total; when following a heavy path, add all the distances along the edges traversed to the running total (as well as the distance along the light edge at the top, if any). The latter can be performed efficiently, along with modifications, if each heavy path is augmented with a data structure such as a segment tree or binary indexed tree (in which the individual array elements correspond to the weights of the edges of the heavy path).
This gives 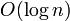 time for queries, since it consists of two "skips" and a LCA query, all of which take logarithmic time or better. It might seem that we have to ascend logarithmically many heavy paths each of which takes logarithmic time, but this is not the case; only the first one, if we start out on it, has to take logarithmic time to query; for the others, which we skip over in their entirety, we can just look up a variable indicating the sum of all weights on that path, which can be updated in constant time when any edge on that path is updated. An update, merely an update to the underlying array structure, takes
time for queries, since it consists of two "skips" and a LCA query, all of which take logarithmic time or better. It might seem that we have to ascend logarithmically many heavy paths each of which takes logarithmic time, but this is not the case; only the first one, if we start out on it, has to take logarithmic time to query; for the others, which we skip over in their entirety, we can just look up a variable indicating the sum of all weights on that path, which can be updated in constant time when any edge on that path is updated. An update, merely an update to the underlying array structure, takes 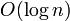 time also.
time also.
References
- Wang, Hanson. (2009). Personal communication.
- D. D. Sleator and R. E. Tarjan, A data structure for dynamic trees, in "Proc. Thirteenth Annual ACM Symp. on Theory of Computing," pp. 114–122, 1981.