Graph theory
A graph is a mathematical object with vertices (also known as nodes), discrete objects, and edges (also known as arcs), relationships between pairs of objects. Because of the wide variety of objects and relationships that may be abstracted as vertices and edges, graphs are highly versatile, and may be used to model a great number of different real-world entities, such as cities and highways, social networks, and the positions of the Rubik's Cube. Likewise, many interesting problems in computer science concern graphs themselves. The subdiscipline of mathematics and computer science concerning graphs is known as graph theory.
Contents
Structure of a graph
Basic structure
Although some graphs may have additional components, all graphs have at least a set of vertices,  , and a set of edges,
, and a set of edges, 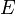 . Each edge is a pair of vertices, say,
. Each edge is a pair of vertices, say,  and
and  , and indicates that some relationship exists between
, and indicates that some relationship exists between  and
and  . We say that this edge is between the vertices
. We say that this edge is between the vertices  and
and  , that it is incident upon
, that it is incident upon  and
and  , or that
, or that  and
and  are connected by the edge, and that the two vertices are adjacent and are neighbors. If there is no edge between
are connected by the edge, and that the two vertices are adjacent and are neighbors. If there is no edge between  and
and  , then no such relationship exists. Take as examples those mentioned in the introduction:
, then no such relationship exists. Take as examples those mentioned in the introduction:
- Given a collection of cities, make each of these cities into a vertex, and if two cities are connected by a highway, connect the two corresponding vertices by an edge. You now have a graph that encodes the network of cities and highways in an abstract way.
- Given a group of people, make each person a vertex, and if two people are friends, connect the two corresponding vertices by an edge. You now have a graph that encodes this social network in an abstract way.
- Let each legal position of the Rubik's Cube be a vertex, and if it is possible to get from one position to another in one move, then connect the two corresponding vertices with an edge. You now have a (very large) graph that encodes all the details of the puzzle.
We usually give vertices names, or labels (often non-negative integers), so that we can distinguish them and remember which vertex is which. Often, to help visualize a problem, we will want to draw a graph on paper. Generally this is done by drawing a dot or a circle for each vertex and drawing a line segment between a pair of dots or pair of circles if and only if there is an edge connecting the corresponding vertices. If we choose to represent the vertices by dots, we generally draw their labels somewhere close by; using circles, we can place them inside, if they are small integers or letters (and hence don't take up too much space.)
Directed and undirected graphs
Some relationships are two-way, but some are only one-way. For example, suppose that in the social network example given in the preceding section, we place an edge between the vertices representing two people if and only if one of them has a crush on the other. The trouble here is that clearly, Alice having a crush on Bob is different than Bob having a crush on Alice, and hence these two scenarios ought to be represented by different graphs. In order to arrange this, we stipulate that each edge also has a direction, and that an edge from  to
to  is not the same as an edge from
is not the same as an edge from  to
to  . A graph that encodes this one-way information is known as a directed graph or digraph, whereas one that does not is an undirected graph. When an edge from
. A graph that encodes this one-way information is known as a directed graph or digraph, whereas one that does not is an undirected graph. When an edge from  to
to  is drawn in the diagram of a graph, generally an arrowhead is added on the end of the line segment representing that edge near
is drawn in the diagram of a graph, generally an arrowhead is added on the end of the line segment representing that edge near  , so that the segment "points" from
, so that the segment "points" from  to
to  . Note that it is possible for two-way relationships to be represented by directed graphs; maybe Alice and Bob secretly have a crush on each other. This would be represented by both edges existing in
. Note that it is possible for two-way relationships to be represented by directed graphs; maybe Alice and Bob secretly have a crush on each other. This would be represented by both edges existing in 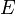 and a double-ended arrow. The point is that directed graphs must be used when it is not guaranteed that all relationships will be bidirectional. An edge from
and a double-ended arrow. The point is that directed graphs must be used when it is not guaranteed that all relationships will be bidirectional. An edge from  to
to  is said to enter
is said to enter  and leave
and leave  . An edge in a directed graph is also known as an arc.
. An edge in a directed graph is also known as an arc.
Weighted graphs
We can endow a graph, be it directed or undirected, with even more structure if we assign a real number to each edge, which is known as a weight, or, depending on the application, length or cost. (The term weight is generic.) Here are some examples of how this may be useful:
- If vertices represent cities and edges represent highways, then let the weight of an edge be the length of time it takes to traverse the corresponding highway (i.e., the time between the two cities corresponding to the vertices that the edge connects).
- If vertices represent warehouses and edges represent shipping routes, let the weight of an edge be the cost of shipping between the warehouses corresponding to the vertices connected by that edge.
A graph in which edges have weight is known as a weighted graph, and one without this information is known as an unweighted graph. Unweighted graphs can often be modelled as weighted graphs in which each edge has weight 1.
In a directed, weighted graph, when edges exist from  to
to  and from
and from  to
to  , these two edges do not necessarily have the same weight.
, these two edges do not necessarily have the same weight.
Simple graphs, multigraphs, and hypergraphs
We have glossed over two subtleties in the above discussion.
First, some graphs may have loops. A loop is an edge that connects a vertex to itself. In many applications of graph theory, loops will not be allowed, but if they are, they are usually not too much of a pain to deal with. (Note that a loop in a directed graph will be drawn with a single arrowhead, not two.) In the mathematical description in the previous section, an edge in an undirected graph with loops will have to be considered a multiset instead of a plain set, as it contains two of the same vertex.
More troublesome than loops are multiple edges connecting a given pair of vertices. In a directed graph, it is normal to have two edges between a pair of vertices, one in each direction, but multiple edges in undirected graphs, or multiple edges in directed graphs in the same direction, can cause problems. First, they cannot be adequately represented with adjacency matrices, although adjacency lists will handle them, and second, the definition of the weight function above will not work, and instead the weight function must be thought of as a function from 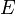 to
to 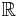 . However, in many applications, multiple edges from one vertex to another can be treated as a single edge whose weight is either the sum, maximum, or minimum of the weights of the multiple edges.
. However, in many applications, multiple edges from one vertex to another can be treated as a single edge whose weight is either the sum, maximum, or minimum of the weights of the multiple edges.
An undirected graph with no loops and no multiple edges is known as a simple graph. A multigraph may have multiple edges, but whether it may contain loops depends on the context.
A hypergraph is a generalization of a graph in which the relationships may involve more than two nodes at a time. They are generally less useful than ordinary graphs.
Representation of graphs
Mathematically
Mathematically, an unweighted graph is considered to be an ordered pair 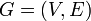 , where
, where  is the set of vertices and
is the set of vertices and 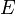 is the set of edges.
is the set of edges.  and
and 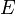 need not be finite. Each element of
need not be finite. Each element of 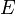 is, of course, a pair of elements from
is, of course, a pair of elements from  . If the graph is directed, then it is an ordered pair, so that
. If the graph is directed, then it is an ordered pair, so that 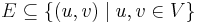 . If the graph is undirected, then it is really an unordered pair, or a set, so that
. If the graph is undirected, then it is really an unordered pair, or a set, so that 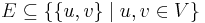 . A weighted graph has an additional component, so that
. A weighted graph has an additional component, so that 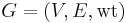 , where
, where 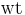 is the weight function,
is the weight function, 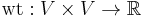 . Here
. Here 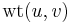 represents the weight of the edge from
represents the weight of the edge from  to
to  , if such an edge exists; otherwise, it is either zero, infinite, or undefined (whichever is most convenient). Note that in an undirected graph,
, if such an edge exists; otherwise, it is either zero, infinite, or undefined (whichever is most convenient). Note that in an undirected graph,  .
.
Adjacency matrix
In programming, there are two main representations of graphs. A graph may be represented by a two-dimensional array, or adjacency matrix, with 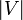 rows and
rows and 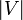 columns, where the entry
columns, where the entry 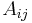 in row
in row  and column
and column  is 1 if an edge from
is 1 if an edge from  to
to  exists, 0 otherwise. In an adjacency matrix for an undirected graph,
exists, 0 otherwise. In an adjacency matrix for an undirected graph, 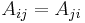 for all
for all 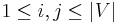 . If the graph is weighted, we often have
. If the graph is weighted, we often have 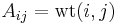 . Thus the adjacency matrix contains enough information to completely reconstruct the graph, and takes up
. Thus the adjacency matrix contains enough information to completely reconstruct the graph, and takes up 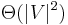 space. It takes only
space. It takes only  time to determine whether two vertices are connected, but it takes
time to determine whether two vertices are connected, but it takes 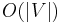 time to retrieve all neighbors of a given vertex, as we have to scan an entire row or column.
time to retrieve all neighbors of a given vertex, as we have to scan an entire row or column.
Adjacency list
The other major representation of the graph is the adjacency list. An adjacency list is actually a collection of 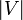 lists of vertices, each of which corresponds to one vertex. The vertex
lists of vertices, each of which corresponds to one vertex. The vertex  will appear in the list of vertex
will appear in the list of vertex  if and only if there is an edge from
if and only if there is an edge from  to
to  . (If the graph is undirected, this means that
. (If the graph is undirected, this means that  will also appear in
will also appear in  's list.) Additional information, such as the weight of the edge, may be stored along with that node in the list. This will now only use
's list.) Additional information, such as the weight of the edge, may be stored along with that node in the list. This will now only use 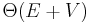 space, and all neighbors of a given node may be retrieved in linear time (i.e., constant time per neighbor). The drawback is that it will take
space, and all neighbors of a given node may be retrieved in linear time (i.e., constant time per neighbor). The drawback is that it will take 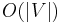 time to determine whether two given nodes are adjacent, since this would require searching through one of their lists.
time to determine whether two given nodes are adjacent, since this would require searching through one of their lists.
In practice, linked lists are not often used; arrays can often be used instead, provided that they only take up as much space as they need to, instead of all having size 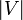 (which is the maximum size that one might have to be). This is easily accomplished using dynamic arrays, such as
(which is the maximum size that one might have to be). This is easily accomplished using dynamic arrays, such as std::vector in C++. If edges are not added or deleted, this also makes it possible to determine whether two given nodes are neighbors in 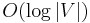 time, by sorting each list and performing binary search.
time, by sorting each list and performing binary search.
Graph-theoretic concepts
The degree of a vertex is the number of edges incident upon it. If the graph is directed, this can be split up into the in-degree, which is the number of edges entering the vertex, and the out-degree, the number of edges leaving it.
A path is a sequence of vertices 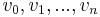 such that for all
such that for all 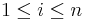 , there is an edge from
, there is an edge from 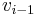 to
to 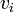 . If such a sequence exists, we say it is a path from
. If such a sequence exists, we say it is a path from 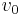 to
to 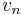 or between
or between 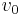 and
and 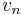 , or that
, or that 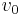 and
and 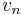 are connected by that path, or that
are connected by that path, or that 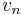 is reachable from
is reachable from 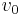 . Note that in a directed graph, saying there is a path from
. Note that in a directed graph, saying there is a path from  to
to  is not the same as saying there is a path from
is not the same as saying there is a path from  to
to  , and the same applies to reachability; if
, and the same applies to reachability; if  and
and  are reachable from each other then they are said to be mutually reachable. We also say that the path visits each of the vertices
are reachable from each other then they are said to be mutually reachable. We also say that the path visits each of the vertices 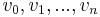 . On a diagram of a graph, a path is obtained by "following" the edges (going only in the directions of arrowheads, if the graph is directed). The length of a path is the number of edges on that path (one less than the number of vertices), and the weight of the path, if the graph is weighted, is the sum of the weights of the edges along that path. (The definition must be slightly modified when multiple edges are allowed.) Note that in some cases length can actually mean weight in a weighted graph; mind the context. A path is said to be a simple path if it does not visit any vertex more than once.
. On a diagram of a graph, a path is obtained by "following" the edges (going only in the directions of arrowheads, if the graph is directed). The length of a path is the number of edges on that path (one less than the number of vertices), and the weight of the path, if the graph is weighted, is the sum of the weights of the edges along that path. (The definition must be slightly modified when multiple edges are allowed.) Note that in some cases length can actually mean weight in a weighted graph; mind the context. A path is said to be a simple path if it does not visit any vertex more than once.
A cycle is a path in which the first and last vertex are the same. By definition, a cycle can never be a simple path, but if it repeats no vertex other than the first and last, it is known as a simple cycle. (An exception is that a simple cycle of length two cannot exist in an undirected graph, since this would use an edge twice.) An odd cycle is a cycle with odd length, whereas an even cycle is a cycle with even length. If a graph has no cycles, it is said to be acyclic.
Types of graphs
A complete graph is one in which an edge exists between every pair of distinct vertices. If it is directed, it will have one each way. A complete directed graph on  vertices has
vertices has 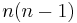 edges (an edge from every vertex to every other). A complete undirected graph on
edges (an edge from every vertex to every other). A complete undirected graph on  vertices, denoted
vertices, denoted 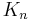 , will have half that many,
, will have half that many, 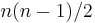 edges.
edges.
Given a graph, if we remove some (possibly zero) vertices and some (possibly zero) edges, we obtain a subgraph. (Note that when a vertex is removed, all edges incident upon it must be removed too.)
An undirected graph is said to be connected if and only if every vertex is reachable from every other vertex. A directed graph is said to be strongly connected if and only if each pair of distinct vertices is mutually reachable. If an undirected graph is not connected, it has two or more subgraphs called connected components. A connected component consists of a vertex and all the vertices reachable from it (and all the incident edges); if two vertices are reachable from each other than they will be in the same connected component, but if not, they will be in different connected components. Put another way, define an equivalence relation on the vertices of the graph so that two vertices are equivalent if and only if one is reachable from the other; then connected components are equivalence classes. If a directed graph is not strongly connected, it has two or more subgraphs called strongly connected components; these are analogous to connected components, and two vertices are in the same strongly connected component if and only if they are mutually reachable. The definition for a strongly connected component in an undirected graph is uncommon will have to be clarified in a problem statement.
A tree is an undirected graph that is both connected and acyclic. A forest is a graph that consists of one or more trees. If a graph is directed and acyclic, it is simply known as a directed acyclic graph or by the initialism DAG. A directed graph that is like a tree, but in which every edge points away from one of the tree's vertices, is called an arborescence.
A bridge or cut edge is an edge that, when removed, causes an increase in the number of connected components of a graph. If a connected graph has no bridges, then it remains connected when any edge is removed, and is said to be edge-connected. If a graph is not edge-connected, it has two or more edge-connected components, defined analogously to connected components; two vertices are in the same edge-connected component if they remain connected when any edge is removed. A cut vertex or articulation point is a vertex that, when removed, causes an increase in the number of connected components. If a connected graph has no articulation points, then it remains connected when any vertex is removed, and is said to be biconnected. If a graph is not biconnected, it has two or more biconnected components, defined analogously to edge-connected components.
Edges may also be spliced or subdivided, which refers to removing an edge and connecting its two vertices via a third vertex inserted "between" them (by adding two new edges). Splicing increases the number of vertices by one and the number of edges by one. If repeated splicing operations on a graph  yield graph
yield graph 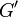 , then
, then 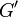 is said to be a subdivision of
is said to be a subdivision of  , and
, and  is said to be a minor of
is said to be a minor of 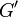 .
.
A flow graph or flow network is a directed graph in which two distinct vertices are specifically denoted the source,  , and the sink,
, and the sink,  , no edges enter
, no edges enter  , and no edges leave
, and no edges leave  . An
. An  -
- cut is a set of edges which, when deleted from a flow graph, cause the sink to become unreachable from the source. As the name suggests, a flow graph is useful for modelling the flow of something (be it concrete or abstract) from the source to sink. For example, a flow network may model a computer network, in which each computer is a vertex and the weight of an edge represents the bandwidth of a cable between two computers.
cut is a set of edges which, when deleted from a flow graph, cause the sink to become unreachable from the source. As the name suggests, a flow graph is useful for modelling the flow of something (be it concrete or abstract) from the source to sink. For example, a flow network may model a computer network, in which each computer is a vertex and the weight of an edge represents the bandwidth of a cable between two computers.
A graph is said to be planar if it is possible to draw it with no edges crossing.
A bipartite graph is a graph in which it is possible to partition the vertices into two sets  and
and  , such that edges exist only between vertices in
, such that edges exist only between vertices in  and vertices in
and vertices in  , with no edges within
, with no edges within  alone or
alone or  alone. This is equivalent to the condition that no odd cycles exist in an undirected graph.
alone. This is equivalent to the condition that no odd cycles exist in an undirected graph.
Graph-theoretic algorithms
Problems relating to trees and bipartite graphs are discussed in the respective articles.
- Finding connected components: Given an undirected graph, label each vertex such that whenever two vertices have the same label, there is a path between them, whereas whenever two vertices have different labels, no such path exists. This can be accomplished in linear time using depth-first search or breadth-first search.
- Shortest path problem: Given two vertices in a graph, find the path of least length (unweighted) or weight (weighted) from one to the other.
- The distance between two nodes is the length (unweighted) or weight (weighted) of the shortest path from one to the other.
- The diameter of a graph is the maximum of the distance function taken over all pairs of nodes. This can be determined by finding all-pairs shortest paths.
- The girth of an unweighted graph is the length of its shortest simple cycle. This can be determined all-pairs shortest paths as well, but in an undirected graph, we have to remember that we cannot go backward along an edge.
- The bounded cost shortest path problem asks us to find the shortest path that does not exceed some fixed cost, where a cost is assigned to each edge in addition to its weight; this is like finding the shortest sequence of flights that fits within one's budget.
- The problem of finding two paths between a given pair of vertices such that they have no common edges and the sum of their weights is minimized can be solved using Suurballe's algorithm.
- Spanning tree: A tree
 is said to span a graph
is said to span a graph  when
when  is a subgraph of
is a subgraph of  and
and  contains all of
contains all of  's vertices. A spanning tree can be found in linear time using depth-first search or breadth-first search.
's vertices. A spanning tree can be found in linear time using depth-first search or breadth-first search.
- Minimum spanning tree problem: The weight of a tree is the sum of the weights of the edges it contains. Find a tree that spans
 , while minimizing its weight. This can be accomplished using a priority-first search instead.
, while minimizing its weight. This can be accomplished using a priority-first search instead. - The minimum diameter spanning tree problem is analogous, but now we want a spanning tree with the lowest possible diameter.
- Minimum spanning tree problem: The weight of a tree is the sum of the weights of the edges it contains. Find a tree that spans
- The minimum spanning arborescence problem is analogous to the minimum spanning tree problem, but more difficult.
- An Eulerian path is a path that uses every edge in a graph exactly once. If it also begins and ends with the same node, it is known as an Eulerian circuit or Eulerian tour. It is possible to determine whether a graph has an Eulerian path or Eulerian tour, and find one if one exists, in linear time.
- A Hamiltonian path or Hamiltonian circuit is defined analogously, but visits every vertex once, instead of visiting every edge once. Detection and construction of Hamiltonian paths/circuits, however, is NP-complete/NP-hard.
- Maximum flow problem: In a flow network, let the weight of an edge represent the capacity of that edge. We want to assign a flow to each edge which is less than or equal to its capacity, such that the sum of all the flows of edges entering any vertex equals the sum of all the flows of edges leaving (so that nothing "accumulates" in a vertex, nor does the vertex "run out"). The exceptions are the source and the sink; the sum of all the flows out of the source equals the sum of all the flows into the sink. We want to assign flows such that this value is maximized.
- Minimum
 -
- cut problem: Instead of regarding the weight of an edge as its capacity, regard it as the cost required to delete that edge. Find an
cut problem: Instead of regarding the weight of an edge as its capacity, regard it as the cost required to delete that edge. Find an  -
- cut of minimum cost.
cut of minimum cost. - Minimum vertex cut problem: Find a subset of a flow graph's vertices, of minimum size, such that removing these vertices from the graph causes the sink to become unreachable from the source. (We are not allowed to remove the source or the sink.) This can be solved by replacing all nodes in the flow graph except the source and the sink by a pair of nodes, one for all the in-edges and one for all the out-edges, with an edge of cost 1 from the in-node to the out-node, and then finding a minimum edge cut, as above. (We set the costs of all other edges to infinity.)
- Minimum cost maximum flow problem: Maximize the flow, but also minimize the cost; the cost of sending flow along an edge is the product of the amount of flow along that edge and some constant specific to that edge.
- Minimum
- Finding strongly connected components: Analogous to finding connected components, but in a directed graph. This is a bit trickier but can still be accomplished in linear time using Kosaraju's algorithm, Tarjan's algorithm, or Gabow's algorithm.
- Finding edge-connected and biconnected components: We can identify all the cut vertices and cut edges of an undirected graph in linear time using a depth-first search algorithm due to Hopcroft and Tarjan.
- Dominators: These are like articulation points, but for directed graphs instead. In a control flow graph with source
 , we say that a vertex
, we say that a vertex  dominates a vertex
dominates a vertex  if every path from
if every path from  to
to  must visit
must visit  . Every vertex dominates itself, but for all
. Every vertex dominates itself, but for all 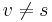 , there is also an immediate dominator
, there is also an immediate dominator  such that
such that 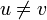 ,
,  dominates
dominates  , and any other dominator of
, and any other dominator of  that is not
that is not  itself also dominates
itself also dominates  . Computing all immediate dominators gives a dominator tree, which can be computed in linear time using the Lengauer–Tarjan algorithm.
. Computing all immediate dominators gives a dominator tree, which can be computed in linear time using the Lengauer–Tarjan algorithm. - A matching is a subset of a graph's edges such that no two edges in the subset have a common vertex. The maximum matching problem is that of finding a matching of a graph with the maximum possible number of edges. A maximum matching can be found in polynomial time using Edmond's matching algorithm.
- A vertex cover is a subset of a graph's vertices such that every edge is incident upon at least one vertex in that subset. The minimum vertex cover problem is that of finding a vertex cover of a graph of minimum size. This problem is NP-hard in general.
- An edge cover is a subset of a graph's edges such that each vertex is an endpoint for at least one edge in that subset. The minimum edge cover problem is that of finding an edge cover of a graph of minimum size. This can be solved by first finding a maximum matching, as above, and then choosing one vertex from each edge in the matching as well as all the remaining vertices. If a matching is also an edge cover, it is called a perfect matching.
- An independent set is a subset of a graph's vertices such that no two vertices in the subset are adjacent. The maximum independent subset problem is that of finding an independent subset of maximum size. This problem is NP-hard.
- It is possible to determine whether a graph is planar in linear time using an algorithm due to Tarjan, but this is extremely complex.