Graph theory
A graph is a mathematical object with vertices, discrete objects, and edges, relationships between pairs of objects. Because of the wide variety of objects and relationships that may be abstracted as vertices and edges, graphs are highly versatile, and may be used to model a great number of different real-world entities, such as cities and highways, social networks, and the positions of the Rubik's Cube. Likewise, many interesting problems in computer science concern graphs themselves. The subdiscipline of mathematics and computer science concerning graphs is known as graph theory.
Basic structure
Although some graphs may have additional components, all graphs have at least a set of vertices,  , and a set of edges,
, and a set of edges, 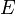 . Each edge is a pair of vertices, say,
. Each edge is a pair of vertices, say,  and
and  , and indicates that some relationship exists between
, and indicates that some relationship exists between  and
and  . We say that this edge is between the vertices
. We say that this edge is between the vertices  and
and  , that it is incident upon
, that it is incident upon  and
and  , or that
, or that  and
and  are connected by the edge. If there is no edge between
are connected by the edge. If there is no edge between  and
and  , then no such relationship exists. Take as examples those mentioned in the introduction:
, then no such relationship exists. Take as examples those mentioned in the introduction:
- Given a collection of cities, make each of these cities into a vertex, and if two cities are connected by a highway, connect the two corresponding vertices by an edge. You now have a graph that encodes the network of cities and highways in an abstract way.
- Given a group of people, make each person a vertex, and if two people are friends, connect the two corresponding vertices by an edge. You now have a graph that encodes this social network in an abstract way.
- Let each legal position of the Rubik's Cube be a vertex, and if it is possible to get from one position to another in one move, then connect the two corresponding vertices with an edge. You now have a (very large) graph that encodes all the details of the puzzle.
We usually give vertices names, or labels (often non-negative integers), so that we can distinguish them and remember which vertex is which. Often, to help visualize a problem, we will want to draw a graph on paper. Generally this is done by drawing a dot or a circle for each vertex and drawing a line segment between a pair of dots or pair of circles if and only if there is an edge connecting the corresponding vertices. If we choose to represent the vertices by dots, we generally draw their labels somewhere close by; using circles, we can place them inside, if they are small integers or letters (and hence don't take up too much space.)