Floating-point data type
Nearly all programming languages provide at least one floating-point data type, intended primarily for the representation of real numbers.[1] A floating-point type must be capable of taking on both positive and negative values, as well as values that are many orders of magnitude greater than unity and values that are many orders of magnitude less than unity. A value of a floating-point data type is often known as a floating-point number, but this term should be used with caution because (unlike integer or real number) it is a purely computational construct and has no natural mathematical equivalent. Some floating-point types, including the most common specification, IEEE 754, support additional values that are not real numbers, such as indeterminate values (a.k.a. Not a Number, or NaN) and infinity.
Floating-point is a generalization of the scientific notation often used to represent very large and very small numbers, for example, the elementary charge in coulombs, 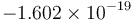 . The decimal point floats, that is, it can correspond to any place in the actual number, as indicated by the exponent. For example, in the number
. The decimal point floats, that is, it can correspond to any place in the actual number, as indicated by the exponent. For example, in the number 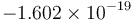 , the decimal point in "1.602" actually represents the position immediately to the right of the nineteenth place after the decimal point when the number is explicitly written out in full form (-0.0000000000000000001^602). Likewise, the decimal point in
, the decimal point in "1.602" actually represents the position immediately to the right of the nineteenth place after the decimal point when the number is explicitly written out in full form (-0.0000000000000000001^602). Likewise, the decimal point in 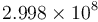 (the speed of light in metres per second) actually represents the place immediately to the left of the eighth decimal place before the decimal point (2^99800000). An exponent of zero means the decimal point is exactly in its actual location.
(the speed of light in metres per second) actually represents the place immediately to the left of the eighth decimal place before the decimal point (2^99800000). An exponent of zero means the decimal point is exactly in its actual location.
A floating-point type represents the number positionally with a variable integer exponent. That is, it represents the number as 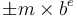 where
where 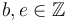 and
and 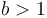 . In our decimal scientific notation, we use
. In our decimal scientific notation, we use 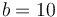 , but computers usually use
, but computers usually use 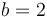 (binary, as usual). Generally, a fixed number of bits of the raw, digital representation of a floating-point type are allocated to representing the exponent
(binary, as usual). Generally, a fixed number of bits of the raw, digital representation of a floating-point type are allocated to representing the exponent  , and a fixed number are allocated to the mantissa (also called the significand),
, and a fixed number are allocated to the mantissa (also called the significand), 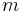 , which is usually constrained to lie in the range
, which is usually constrained to lie in the range 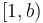 to ensure (somewhat) unique representation. The consequence of this is that the number of significant figures in a floating-point number is generally independent of its magnitude. This is ideal for scientific computation, in which the magnitudes of quantities often have no real meaning but are simply a relic of the system of units used to represent them.
to ensure (somewhat) unique representation. The consequence of this is that the number of significant figures in a floating-point number is generally independent of its magnitude. This is ideal for scientific computation, in which the magnitudes of quantities often have no real meaning but are simply a relic of the system of units used to represent them.
Floating-point imprecision[edit]
Floating-point data types cannot exactly store irrational numbers like 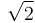 or
or 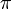 . Nor can they exactly represent numbers that have non-terminating expansions in base
. Nor can they exactly represent numbers that have non-terminating expansions in base  , such as
, such as 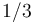 when
when 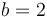 (or even
(or even 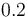 , which terminates in base 10 but not in base 2). Thus:
, which terminates in base 10 but not in base 2). Thus:
- Tests for equality among floating-point numbers should not be used. The test
sqrt(2.0) * sqrt(2.0) == 2.0(in C) may evaluate to 0 (false), for example. Always test using absolute or relative tolerances instead (for example,fabs(x-y) < 1e-8instead ofx == y). - Avoid using floating-point numbers if possible. For example, it might be wise to store currency values in fixed-point format; $12.95 could be represented by the integer 1295, instead of the floating-point number 12.95 (which is probably inexact). If
xandyare integers, testx*x == yinstead ofx == sqrt(y). The very common test(double)a/b == (double)c/d(with all variables integral) should be replaced witha*d == b*c.
Floating-point types by language[edit]
This section is in need of expansion.
Most implementations of most programming languages support at least one floating-point type that corresponds to either the binary32 or the binary64 type of IEEE 754 (q.v. for references).
| Language | IEEE 754 binary32 type | IEEE 754 binary64 type | Other floating-point types | Notes |
|---|---|---|---|---|
| C and C++ | Often float (and float _Complex)
|
Often double (and double _Complex)
|
long double (and long double _Complex)
|
The standard is completely silent on the ranges of float, double, and long double, except to prescribe that long double be "longer" than double (its range must be a superset, not necessarily proper) which in turn must be "longer" than float. The _Complex types were added in C11.[2]
|
| Java | float
|
double
|
||
| JavaScript | Number
|
|||
| Haskell | Often Float and Complex Float
|
Often Double and Complex Double
|
One is free to define custom floating-point types according to the Floating type class definition.
| |
| .NET | System.Single
|
System.Double
|
||
| O'Caml | float
|
|||
| Pascal | single
|
double
|
real, extended
|
See IEEE 754 for discussion. The real type on Turbo Pascal was actually a software-emulated 48-bit type, wider than binary32 but narrower than binary64, whereas in Free Pascal it maps to either single or double. The extended type in Turbo Pascal maps to the 80-bit extended type native to Intel FPUs (see long double); this is also true of Free Pascal when the target is Intel x86 or x86-64; otherwise extended maps to double. The comp type introduced in Turbo Pascal was not really a floating-point type, but a signed 64-bit non-ordinal integral type. However, direct support for 64-bit integers did not exist on all the architectures supported by Turbo Pascal; instead, the significand part of an extended had to be used, since it is 64 bits long.
|
| Python | types.FloatType, types.ComplexType
|
The nature of FloatType is left up to the implementation.
|
References[edit]
- ↑ Some programming languages may also have built-in support for complex floating-point types, but it is worth emphasizing that they invariably represent the complex floating-point number internally as a pair of real floating-point numbers.
- ↑ see draft http://www.open-std.org/jtc1/sc22/wg14/www/docs/n1570.pdf